|
|
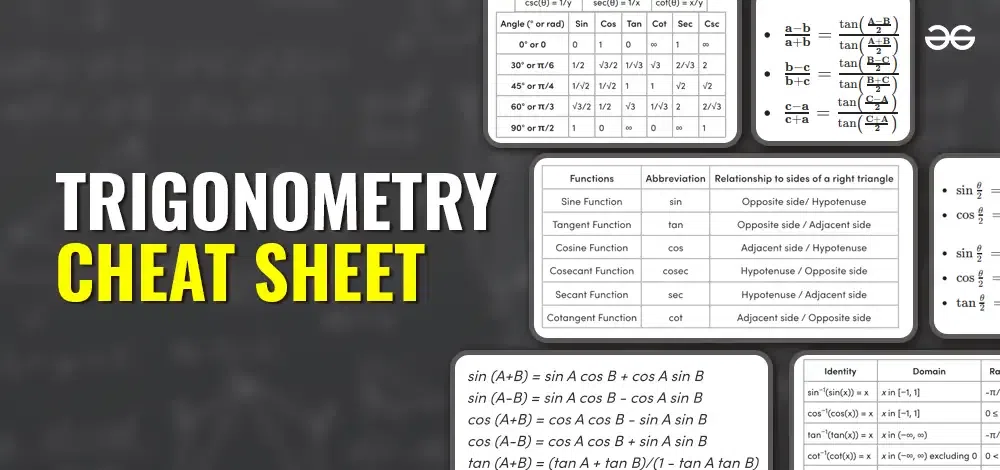
Trigonometry is the branch of mathematics that studies the relationships between the angles and sides of triangles. However, trigonometry can also be challenging to learn and remember, especially when dealing with complex problems and formulas. That is why having a trigonometric cheat sheet can be very helpful for students, teachers, and anyone who wants to refresh their knowledge of trigonometry. A trigonometric cheat sheet is a concise summary of the most important concepts, identities, formulas, and graphs of trigonometry. In this article, we will provide you with a comprehensive trigonometric cheat sheet that covers everything you need to know about trigonometry, from the definitions of the trigonometric functions and ratios, to the laws of sines and cosines, to the inverse and hyperbolic functions, and more.  What is a Right-Angled Triangle?Right triangle, also known as a right-angled triangle, is a triangle that contains an angle measuring 90°. The side opposite to the right angle is called the hypotenuse, while the sides adjacent to the right angle are called adjacent and opposite sides.  Trigonometric RatiosSix trigonometric Ratios are:
Unit CircleA unit circle is a circle with a radius of 1. 
Trigonometry TableTable for all trigonometric ratios for some specific values is:
Read More about Trigonometric Table. Trigonometric Identities
Some of these important identities are discussed below: Reciprocal Trigonometric IdentitiesIn all trigonometric ratios, there is a reciprocal relation between a pair of ratios, which is given as follows:
Pythagorean Trigonometric IdentitiesPythagorean trigonometric identities are based on the Right-Triangle theorem or Pythagoras theorem, and are as follows:
Trigonometric Ratio IdentitiesAs tan and cot are defined as the ratio of sin and cos, which is given by the following identities:
Trigonometric Identities of Opposite AnglesIn trigonometry angle measured in the clockwise direction is measured in negative parity and all trigonometric ratios defined for negative parity of angle are defined as follows:
Complementary Angles IdentitiesComplementary angles are the pair of angles whose measure add up to 90°. Now, the trigonometric identities for complementary angles are as follows:
Supplementary Angles IdentitiesSupplementary angles are the pair of angles whose measure add up to 180°. Now, the trigonometric identities for supplementary angles are:
Periodicity of Trigonometric FunctionTrigonometric functions such as sin, cos, tan, cot, sec, and cosec all are periodic in nature and have different periodicity. The following identities for the trigonometric ratio explain their periodicity.
Sum and Difference IdentitiesTrigonometric identities for Sum and Difference of angle include the formulas such as sin(A+B), cos(A-B), tan(A+B), etc.
Note: Identities for sin (A+B), sin (A-B), cos (A+B), and cos (A-B) are called Ptolemy’s Identities. Double Angle Identities
Half Angle FormulasUsing double-angle formulas, half-angle formulas can be calculated. To calculate half-angle formulas replace θ with θ/2 then,
Some more Half Angle IdentitiesOther than the above-mentioned identities, there are some more half-angle identities which are as follows:
Product-Sum IdentitiesThe following identities state the relationship between the sum of two trigonometric ratios with the product of two trigonometric ratios.
Products IdentitiesProduct Identities are formed when we add two of the sum and difference of angle identities and are as follows:
Triple Angle FormulasOther than double and half angle formulas, there are identities for trigonometric ratios which are defined for triple angle. These identities are as follows:
Relation between Angles and Sides of TriangleThree rules which related the sides of triangles to the interior angles of triangles are,
If a triangle ABC with sides a, b, and c which are sides opposites to the ∠A, ∠B, and ∠C respectively, then #Image Sine RuleSine rule states the relationship between sides and angles of the triangle which is the ratio of side and sine of angle opposite to the side always remains the same for all the angles and sides of the triangle and is given as follows:
Cosine RuleCosine Rule involves all the sides, and one interior angle of the triangle is given as follows:
Tangent Rule
Also, Read Inverse Trigonometric FunctionsInverse trigonometric functions are the inverse functions of the trigonometric functions such as sine, cosine, tangent, cotangent, secant, and cosecant.
Domain and RangeDomain and range of inverse trigonometric functions are:
Inverse Trigonometric IdentitiesSome basic identities are:
Other identities includes:
|
Reffered: https://www.geeksforgeeks.org
| Mathematics |
Type: | Geek |
Category: | Coding |
Sub Category: | Tutorial |
Uploaded by: | Admin |
Views: | 24 |