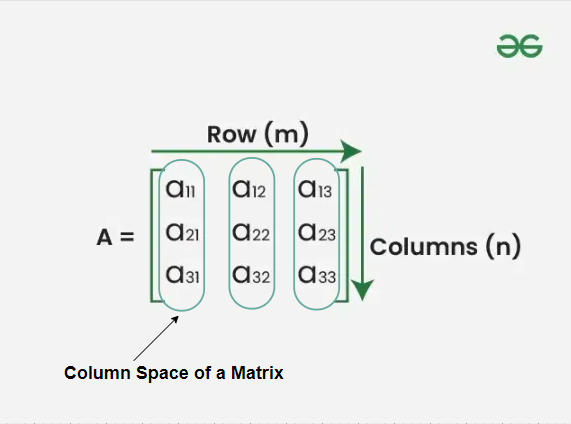
The concept of the column space of any specific matrix may well be considered one of the simplest ideas in linear algebra and is, without doubt, one of the crucial ideas in the study of the solutions to linear systems and in the manner that promotes understanding of the effects of linear transformations in the given vector space.

In this article, the main focus will be on illustrating a concept of how one would go about finding the column space of a particular matrix.

What is Column Space of a Matrix?

The column space of a matrix A, also referred to as a range(A), denoted by C(A) is defined as the set of all linear combinations of the given matrix A or more formally it is defined as the number of columns of A. Applications of the idea of column space include those giving information about the rank of the matrix ‘A’, solutions of systems of linear equations and properties of linear transformation.

The relevance of the column space is also vast in engineering, computer science, and statistics because it is used to solve differential equations and analyze and design algorithms.

Column Space of a Matrix

Example of Column Space of a Matrix

[Tex]A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} [/Tex]

To find the column space of A, we look at the linear combinations of its column vectors:

[Tex]\mathbf{v}_1 = \begin{bmatrix} 1 \\ 4 \\ 7 \end{bmatrix}, \quad \mathbf{v}_2 = \begin{bmatrix} 2 \\ 5 \\ 8 \end{bmatrix}, \quad \mathbf{v}_3 = \begin{bmatrix} 3 \\ 6 \\ 9 \end{bmatrix}[/Tex]

The column space is the span of [Tex]{v_1, v_2, v_3}[/Tex], which represents all vectors that can be expressed as [Tex] c_1v_1 + c_2v_2 + c_3v_3,[/Tex] where [Tex]c_1, c_2, and c_3[/Tex] are scalars.

Methods to Find Column Space of a Matrix

To find the column space of a matrix, the following methods may be used. Here, we will provide an overview of three primary methods:

• Using Gaussian Elimination
• Using Reduced Row Echelon Form or RREF
• Using Singular Value Decomposition or SVD

Each method involves systematic steps to transform the matrix and identify its column space.

Method 1: Using Gaussian Elimination

Gaussian Elimination is a method used to convert a matrix into its row echelon form or REF. Here are the detailed steps:

Convert Matrix to REF:

• Start with matrix A.
• Use row operations (swap rows, multiply a row by a non-zero scalar, add/subtract multiples of rows) to convert A into REF.

Identify Pivot Columns:

• The pivot columns in the REF correspond to the linearly independent columns in the original matrix A.
• These pivot columns form the basis for the column space.

Example: Consider the matrix A:

[Tex]A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} [/Tex]

Perform row operations to convert A into REF:

[Tex]\begin{bmatrix} 1 & 2 & 3 \\ 0 & -3 & -6 \\ 0 & 0 & 0 \end{bmatrix} [/Tex]

The pivot columns are the first and second columns of A, hence the basis for the column space is:

.[Tex]\left\{ \begin{bmatrix} 1 \\ 4 \\ 7 \end{bmatrix}, \begin{bmatrix} 2 \\ 5 \\ 8 \end{bmatrix} \right\} [/Tex]

Method 2: By using Reduced Row Echelon Form (RREF)

Reduced Row Echelon Form or RREF is a simplified version of REF where each pivot is 1 and is the only non-zero entry in its column. The steps are:

Convert Matrix to RREF:

• Start with matrix A.
• Apply row operations to transform A into RREF.

Select Pivot Columns:

• Identify the pivot columns in the RREF.
• These correspond to the linearly independent columns in the original matrix A.

Example: Consider the matrix A:

[Tex]A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} [/Tex]

Convert A to RREF:

[Tex]\begin{bmatrix} 1 & 0 & -1 \\ 0 & 1 & 2 \\ 0 & 0 & 0 \end{bmatrix} [/Tex]

Pivot columns are the first and second columns of A, hence the basis for the column space is:

[Tex]\left\{ \begin{bmatrix} 1 \\ 4 \\ 7 \end{bmatrix}, \begin{bmatrix} 2 \\ 5 \\ 8 \end{bmatrix} \right\} [/Tex]

Method 3: By using Singular Value Decomposition or SVD

Singular Value Decomposition or SVD is the procedure that breaks the matrix A into other three matrices commonly known as; U, Σ, and V^T. The steps are:

Perform SVD:

• To decompose A, we have A = U ΣV^T where U and V are orthogonal matrices while Σ is a diagonal matrix.

Identify Column Space:

• The column space of A is spanned by the columns of U corresponding to the non-zero singular values in Σ.

Example: Consider the matrix A:

[Tex]A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} [/Tex]

Perform SVD to get:

[Tex]U = \begin{bmatrix} -0.214 & 0.887 & 0.408 \\ -0.520 & 0.249 & -0.817 \\ -0.826 & -0.389 & 0.408 \end{bmatrix}[/Tex]

[Tex]\Sigma = \begin{bmatrix} 16.848 & 0 & 0 \\ 0 & 1.068 & 0 \\ 0 & 0 & 0 \end{bmatrix} [/Tex]

[Tex]V^T = \begin{bmatrix} -0.479 & -0.572 & -0.665 \\ -0.776 & -0.075 & 0.627 \\ -0.408 & 0.816 & -0.408 \end{bmatrix} [/Tex]

Therefore, the corresponding columns in the matrix U are the basis for the column space of A, namely, 16.848 and 1.068.

Applications of Column Space of a Matrix

The applications of column space of a Matrix:

• Solving Linear Systems: Identifies if a system of equations has solutions and determines their nature.

• Data Compression: In techniques like PCA, the column space helps reduce the dimensions of data while preserving significant features.

• Control Theory: Used in designing control systems by determining state reachability and observability.

• Signal Processing: Helps in filtering and reconstructing signals.

• Machine Learning: In algorithms like SVD for recommendation systems and latent semantic analysis.

Conclusion

It is thus important to come up with a good comprehension of the column space of a matrix for different applications in linear algebra as well as others. Understanding how to use methods like Gaussian Elimination, RREF, and SVD, can help students find any matrix’s column space. This helps in solving engineering problems, data analysis and many others; it is therefore an essential part of the mathematics system.

Also Read:

• Inverse of 3×3 Matrix
• Covariance of Matrix

Examples on column space of a matrix

Example 1: Find the column space of the matrix A:

[Tex]A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} [/Tex]

Solution:

Convert to Row Echelon Form (REF):

Perform row operations to get REF:

[Tex]\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} [/Tex]

Row operations:

• R₂→R₂ − 3R₁
• R₃→R₃ − 5R₁

Resulting in:

[Tex]\begin{bmatrix} 1 & 2 \\ 0 & -2 \\ 0 & -4 \end{bmatrix}[/Tex]

Further, R3←R3 − 2R2:

[Tex]\begin{bmatrix} 1 & 2 \\ 0 & -2 \\ 0 & 0 \end{bmatrix}[/Tex]

Identify Pivot Columns:

Pivot columns are the first and second columns.

Column Space:

Basis for the column space is:

[Tex]\left\{ \begin{bmatrix} 1 \\ 3 \\ 5 \end{bmatrix}, \begin{bmatrix} 2 \\ 4 \\ 6 \end{bmatrix} \right\} [/Tex]

Example 2: Find the column space of the matrix B:

[Tex]B = \begin{bmatrix} 2 & 4 & 1 \\ 0 & 3 & -1 \\ -2 & 1 & 5 \end{bmatrix} [/Tex]

Solution:

Convert to Reduced Row Echelon Form (RREF):

Perform row operations to get RREF:

[Tex]B = \begin{bmatrix} 2 & 4 & 1 \\ 0 & 3 & -1 \\ -2 & 1 & 5 \end{bmatrix} [/Tex]

Row operations:

• R₃ → R₃ + R₁
• R₂ → R₂/3
• R₁ → R₁ − 2R₂
• R₃ → R₃ − 4R₂

Resulting in:

[Tex]\begin{bmatrix} 2 & 0 & 3 \\ 0 & 1 & -\frac{1}{3} \\ 0 & 0 & 8 \end{bmatrix} [/Tex]

Further, R₁ → R₁/2, R₃ → R₃/8:

[Tex]\begin{bmatrix} 1 & 0 & 1.5 \\ 0 & 1 & -\frac{1}{3} \\ 0 & 0 & 1 \end{bmatrix} [/Tex]

Identify Pivot Columns:

Pivot columns are the first, second, and third columns.

Column Space:

The basis for the column space is:

[Tex]\left\{ \begin{bmatrix} 2 \\ 0 \\ -2 \end{bmatrix}, \begin{bmatrix} 4 \\ 3 \\ 1 \end{bmatrix}, \begin{bmatrix} 1 \\ -1 \\ 5 \end{bmatrix} \right\} [/Tex]

Example 3: Find the column space of the matrix C using Singular Value Decomposition (SVD):

[Tex]C = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ 1 & 1 & 1 \end{bmatrix} [/Tex]

Solution:

Perform SVD:

Decompose C into U, Σ, and V^T.

Suppose U, Σ, and V^T are obtained as:

[Tex]U = \begin{bmatrix} 0.5 & -0.5 & -0.5 & 0.5 \\ 0.5 & 0.5 & -0.5 & -0.5 \\ 0.5 & 0.5 & 0.5 & 0.5 \\ 0.5 & -0.5 & 0.5 & -0.5 \end{bmatrix} [/Tex]

[Tex]\Sigma = \begin{bmatrix} 1.732 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix} [/Tex]

[Tex]V^T = \begin{bmatrix} 0.577 & 0.577 & 0.577 \\ 0.707 & 0 & -0.707 \\ 0 & 1 & 0 \end{bmatrix} [/Tex]

Identify Column Space:

The non-zero singular values in Σ are 1.732 and 1. The corresponding columns of U form the basis for the column space.

Column Space:

The basis for the column space is:

[Tex]\left\{ \begin{bmatrix} 0.5 \\ 0.5 \\ 0.5 \\ 0.5 \end{bmatrix}, \begin{bmatrix} -0.5 \\ 0.5 \\ 0.5 \\ -0.5 \end{bmatrix} \right\}[/Tex]

Practice Problems on Column Space of a Matrix

P1. Find the column space of the matrix D:

[Tex]D = \begin{bmatrix} 1 & 2 \\ 3 & 6 \\ 2 & 4 \end{bmatrix} [/Tex]

P2. Find the column space of the matrix E using RREF:

[Tex]E = \begin{bmatrix} 1 & 3 & 2 \\ 2 & 6 & 4 \\ 1 & 2 & 1 \end{bmatrix} [/Tex]

P3. Find the column space of the matrix F using Gaussian Elimination:

[Tex]F = \begin{bmatrix} 2 & 1 & 4 \\ 1 & 3 & 2 \\ 0 & 2 & 3 \end{bmatrix} [/Tex]

P4. Find the column space of the matrix G using SVD:

[Tex]G = \begin{bmatrix} 1 & 1 \\ 0 & 1 \\ 1 & 0 \\ 1 & 1 \end{bmatrix} [/Tex]

FAQs on Column Space of a Matrix

What does the column space of a matrix tell us?

Column space of a matrix is defined to be the set of all vectors that can be obtained by carrying out linear operation on these vectors and is more interested in where these vectors are.

How to check if a vector is in the column space of a matrix?

To check if a given vector is contained in the column space or not, the operation Ax=b is carried out; any vector which can satisfy the said equation is part of the column space.

What is the null space of a matrix column space?

The null space of the matrix is the set of vector which when added to the given matrix or operated on by it yields a zero vector and is not equal to the column vector space.

What is the column space geometrically?

In terms of geometry, the column space is an isolate, a subspace in the vector space, within which the columns of the matrix are located.

Can a vector be in both column space and null space?

Well, a given vector cannot be simultaneously a part of the column space and null space of the same matrix since their intersection is the zero vector only.