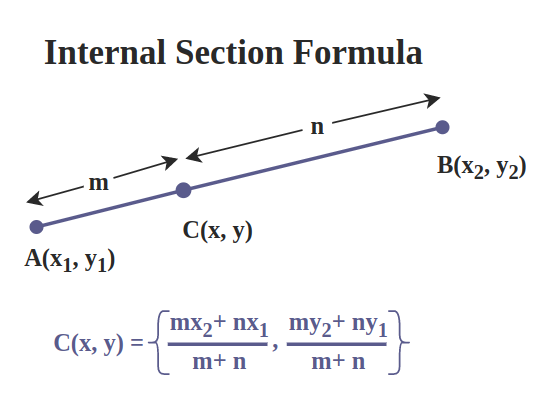
The Division of a Line Segment is one of the basic concepts in geometry that helps to understand different principles. It is the process of determining a point that will split a given line segment into the desired ratio either inside or outside the original line segment.

This article consists of solved problems which will help the learners to understand the basics more firmly.

What is Division of a Line Segment?

Division of a line segment encompasses the procedure of finding a point that cuts a line segment in some specific ratio. This means that can be done internally meaning the point lies between both ends/endpoint or externally meaning that the point is outside the segment. Besides, this concept is widely applied in coordinate geometry, constructions, and proof of different geometrical problems; therefore, its understanding is vital.

Important Formulas/Concepts

Some of the most important formulas and concepts for the Division of Line Segments are as follows:

Section Formula

The section formula is used to find the coordinates of a point that divides a line segment joining two points [Tex] (x_1, y_1) [/Tex] and [Tex] (x_2, y_2)[/Tex] in a given ratio m:n. If a point P(x, y) divides the line segment in the ratio m:n.

In this case, the coordinates of P can be determined by the following formulas:

[Tex]P(x, y) = \left( \frac{mx_2 + nx_1}{m + n}, \frac{my_2 + ny_1}{m + n} \right)[/Tex]

Midpoint Formula

The midpoint formula falls under the section formula with one of the ratios being 1. It is used to determine the coordinates of the midpoint M of a line segment passing through two points; (x₁, y₁) and (x₂, y₂).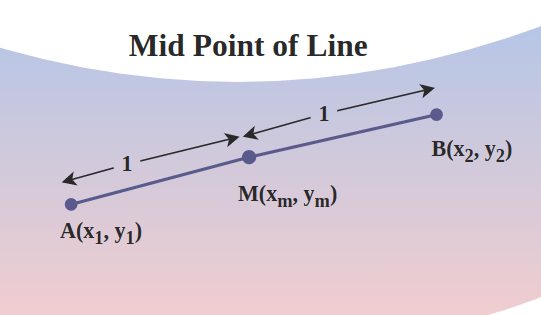

The coordinates of the midpoint are given by:

[Tex]M(x, y) = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)[/Tex]

Ratio of Division

The concept of the ratio of division involves understanding both internal and external divisions of a line segment. In internal division, a point P divides a line segment AB internally in the ratio m:n, and its coordinates can be found using the section formula mentioned above. In external division, the point P divides the line segment externally in the ratio m:n, and its coordinates are given by:

[Tex]P(x, y) = \left( \frac{mx_2 – nx_1}{m – n}, \frac{my_2 – ny_1}{m – n} \right)[/Tex]

Division of a Line Segment Practice Problems

Problem 1: Find the coordinates of the point P that divides the line segment joining (2,3) and (8,7) in the ratio 2:3.

Solution:

Using the section formula for internal division:

[Tex]P(x, y) = \left( \frac{m x_2 + n x_1}{m + n}, \frac{m y_2 + n y_1}{m + n} \right)[/Tex]

Given [Tex](x_1, y_1) = (2,3), (x_2, y_2) = (8,7)[/Tex], and ratio m:n=2:3,

[Tex]P(x, y) = \left( \frac{2 \cdot 8 + 3 \cdot 2}{2 + 3}, \frac{2 \cdot 7 + 3 \cdot 3}{2 + 3} \right) \\= \left( \frac{16 + 6}{5}, \frac{14 + 9}{5} \right) \\= \left( \frac{22}{5}, \frac{23}{5} \right) ~=~ \left( 4.4, 4.6 \right)[/Tex]

So, the coordinates of P are (4.4,4.6).

Problem 2: Find the coordinates of the point Q that divides the line segment joining (1,2) and (5,6) externally in the ratio 3:1.

Solution:

Using the section formula for external division:

[Tex]Q(x, y) = \left( \frac{m x_2 – n x_1}{m – n}, \frac{m y_2 – n y_1}{m – n} \right)[/Tex]

Given [Tex] (x_1, y_1) = (1,2), (x_2, y_2) = (5,6)[/Tex], and ratio m:n=3:1,

[Tex]Q(x, y) = \left( \frac{3 \cdot 5 – 1 \cdot 1}{3 – 1}, \frac{3 \cdot 6 – 1 \cdot 2}{3 – 1} \right) \\= \left( \frac{15 – 1}{2}, \frac{18 – 2}{2} \right) \\=~ \left( \frac{14}{2}, \frac{16}{2} \right) = \left( 7, 8 \right)[/Tex]

So, the coordinates of Q are (7,8).

Problem 3: Find the midpoint M of the line segment joining (3,4) and (7,8).

Solution:

Using the midpoint formula:

[Tex]M(x, y) = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)[/Tex]

Given [Tex](x_1, y_1) = (3,4), (x_2, y_2) = (7,8),[/Tex]

[Tex]M(x, y) = \left( \frac{3 + 7}{2}, \frac{4 + 8}{2} \right) = \left( \frac{10}{2}, \frac{12}{2} \right) = \left( 5, 6 \right)[/Tex]

So, the midpoint M is (5,6).

Problem 4: Find the coordinates of the point R that divides the line segment joining (-3,-2) and (5,4) in the ratio 3:4.

Solution:

Using the section formula for internal division:

[Tex]R(x, y) = \left( \frac{m x_2 + n x_1}{m + n}, \frac{m y_2 + n y_1}{m + n} \right)[/Tex]

Given [Tex](x_1, y_1) = (-3,-2), (x_2, y_2) = (5,4)[/Tex], and ratio m:n=3:4,

[Tex]R(x, y) = \left( \frac{3 \cdot 5 + 4 \cdot (-3)}{3 + 4}, \frac{3 \cdot 4 + 4 \cdot (-2)}{3 + 4} \right) = \left( \frac{15 – 12}{7}, \frac{12 – 8}{7} \right) = \left( \frac{3}{7}, \frac{4}{7} \right)[/Tex]

So, the coordinates of R are (3/7, 4/7).

Problem 5: Find the coordinates of the point S that divides the line segment joining (-4,3) and (6,-2) externally in the ratio 5:2.

Solution:

Using the section formula for external division:

[Tex]S(x, y) = \left( \frac{m x_2 – n x_1}{m – n}, \frac{m y_2 – n y_1}{m – n} \right)[/Tex]

Given [Tex](x_1, y_1) = (-4,3), (x_2, y_2) = (6,-2)[/Tex], and ratio m:n=5:2,

[Tex]S(x, y) = \left( \frac{5 \cdot 6 – 2 \cdot (-4)}{5 – 2}, \frac{5 \cdot (-2) – 2 \cdot 3}{5 – 2} \right) = \left( \frac{30 + 8}{3}, \frac{-10 – 6}{3} \right) = \left( \frac{38}{3}, \frac{-16}{3} \right)[/Tex]

So, the coordinates of S are (38/3, -16/3).

Problem 6: In triangle ABC, A(1,2), B(4,5), and C(7,8). Find the coordinates of the centroid G.

Solution:

The centroid G of a triangle with vertices

[Tex](x_1, y_1), (x_2, y_2), and (x_3, y_3)[/Tex] is given by:

[Tex]G(x, y) = \left( \frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3} \right)[/Tex]

Given [Tex] (x_1, y_1) = (1,2), (x_2, y_2) = (4,5), (x_3, y_3) = (7,8)[/Tex]

[Tex]G(x, y) = \left( \frac{1 + 4 + 7}{3}, \frac{2 + 5 + 8}{3} \right) = \left( \frac{12}{3}, \frac{15}{3} \right) = \left( 4, 5 \right)[/Tex]

So, the coordinates of the centroid G are (4,5).

Problem 7: A city is located at (3,4) and a town is located at (9,12). Find the coordinates of the point on the road connecting the city and town that is twice as close to the town as it is to the city.

Solution:

Given the ratio 1:2 (since the point is twice as close to the town), we use the section formula for internal division:

[Tex]P(x, y) = \left( \frac{m x_2 + n x_1}{m + n}, \frac{m y_2 + n y_1}{m + n} \right)[/Tex]

Given [Tex](x_1, y_1) = (3,4), (x_2, y_2) = (9,12)[/Tex], and ratio m:n=2:1,

[Tex]P(x, y) = \left( \frac{2 \cdot 9 + 1 \cdot 3}{2 + 1}, \frac{2 \cdot 12 + 1 \cdot 4}{2 + 1} \right) = \left( \frac{18 + 3}{3}, \frac{24 + 4}{3} \right) = \left( \frac{21}{3}, \frac{28}{3} \right) = \left( 7, \frac{28}{3} \right)[/Tex]

So, the coordinates of the point are (7, 28/3).

Division of a Line Segment: Worksheet

Q1. Find the coordinates of the point P that divides the line segment joining (1,2) and (3,4) in the ratio 3:2.

Q2. Determine the point Q that divides the line segment joining (4,-2) and (-1,3) externally in the ratio 2:1.

Q3. Calculate the midpoint of the line segment joining (2,5) and (8,-3).

Q4. Find the coordinates of the point R that divides the line segment joining (6,2) and (-4,-3) in the ratio 4:1.

Q5. Determine the coordinates of the point S that divides the line segment joining (7,-5) and (2,3) externally in the ratio 3:4.

Q6. A point T divides the line segment joining (5,6) and (-3,2) in the ratio 1:3. Find the coordinates of T.

Q7. Find the coordinates of the centroid of a triangle with vertices (1,1), (4,5), and (7,-1).

Q8. A point U divides the line segment joining (0,0) and (10,10) in the ratio 5:3. Find the coordinates of U.

Q9. Calculate the coordinates of the point that divides the line segment joining (8,-4) and (-2,6) in the ratio 2:5.

Q10. Determine the coordinates of the point that is equidistant from (1,2) and (7,8).

Answer Key:

1. (2.2, 3.2)
2. (6, -8)
3. (5, 1)
4. (4, 1)
5. (-5, 9)
6. (2, 5)
7. (4, 1.67)
8. (6.25, 6.25)
9. (4, -1)
10. (4, 5)

Conclusion

Any student who wishes to do well in geometry must be very conversant with the division of a line segment. This way, when solving different problems, a student develops a better view of the concept and its possibilities. This particular article presents a list of problems for students to solve and certain methods to follow to prepare easily for other geometric problems.

FAQs on Division of Line Segments

What can a line segment be divided into?

A line segment can be divided into smaller segments or points using specific ratios or at certain points.

What is the point of division of a line segment?

The point of division is a specific point on the line segment that splits it into two parts according to a given ratio.

How do you separate a line segment into various sections?

You can separate a line segment into various sections by marking points on it based on given distances or ratios.

Can line segments be parts of lines?

Yes, line segments are parts of lines; they are the portions of lines between two endpoints.

What do the line segments represent?

Line segments represent the shortest distance between two points and are used to measure or connect points in geometry.