
|
|
Large numbers extend beyond our everyday figures, offering insights into math and science. They help us understand vast concepts like the number of stars or distances in the universe. We’ll explore examples like 1 Lakh, 1 Million, and 1 Billion, and learn how to write and use these numbers. Large numbers are crucial in computer science, physics, chemistry, and more. Concepts like infinity and its sizes challenge our usual ways of thinking. Table of Content What are Large Numbers?As we know, when we write a number, we divide it into groups and write it with commas (,) for better intuition of its value and readability. The groups are as follows- ones, tens, hundreds, thousands, millions, billions and so on. Again, each of these is divided into subgroups except ones, tens, and hundreds. These sub-divisions are as given in Figure 1. These groups were according to the “Internation Number System”.  International Number System Now, let us understand how to read such numbers with an example: 4,747 will be read as “four thousand, seven hundred, and forty-seven”. See where the comma (,) is placed in the given example and compare it with the groups given in Figure 1. In this case its place resembles the one given for Thousands and has only three digits after that which can be used to understand intuitively that this must be of a thousand group. This is one reason for placing commas while writing large numbers: it helps you instantly recognise the groups and how to read them without the hassle of counting the places of the digits. For Example: 10,948,393,830 is read as “ten billion, nine hundred forty-eight million, three hundred ninety-three thousand, eight hundred thirty.” As you can see, the first three groups (i.e., up to the hundreds) are written without commas. After the first comma from the right, you reach the thousands group. Up to the second comma, it remains in the thousands group, and beyond that, you enter the millions group, and so on. Meaning of Large NumbersLarge numbers are those above one million, often represented with exponents [Tex]{\mathbf{10}}^\mathbf{9}[/Tex] or in terms such as billion or thousand million, which can vary by system. In the American system, each denomination above 1,000 million (i.e., one billion) is 1,000 times the previous one (e.g., one trillion = 1,000 billions; one quadrillion = 1,000 trillions). Conversely, the British system historically made each denomination 1,000,000 times the preceding one (e.g., one trillion = 1,000,000 billions), except for the term “milliard,” sometimes used for 1,000 million. Till 1 billion it’s same for both the systems.
As you can see there are multiple ways to read the large numbers based on system or region. So, to avoid confusion there is a better way which is accepted worldwide and easy to understand. When a number is made of more than 12 figures, we can use the following way or system:
Operations on Large NumbersThere are various techniques for carrying out mathematical operations on large numbers. Let’s explore the basic operations: Addition of Large NumbersAdding large numbers involves the same basic principles as adding smaller numbers, but requires careful alignment of each digit and handling of carryovers. Here’s a detailed example: Example: [Tex]\mathbf{947},\mathbf{255},\mathbf{821}+\mathbf{133},\mathbf{446},\mathbf{989}[/Tex]. Subtraction of Large NumbersSubtracting large numbers follows a similar process, but involves borrowing. Here’s a detailed example: Example: [Tex]\mathbf{947},\mathbf{255},\mathbf{821}-\mathbf{133},\mathbf{446},\mathbf{989}[/Tex]. Multiplication of Large NumbersMultiplying large numbers can be performed using long multiplication or more advanced techniques like the Karatsuba algorithm for efficiency. Here’s a detailed example using long multiplication: Example: [Tex]\mathbf{123},\mathbf{456}\ \times\ \mathbf{789}[/Tex].  Multiplication of Large Numbers Division of Large NumbersThe best way to do it manually is through the “Long Division Method”. Just like for smaller numbers. Write the dividend (5,393,823,904) under the long division bar and the divisor (1,552) outside the bar. Example: Divide 5,393,823,904 by 1,552 Solution:  Division of Large Numbers Therefore, the answer is “3,475,402”. Large Numbers in Real LifeBig numbers are more than just abstract ideas; they are essential to many facets of daily life as well as to many scientific and technological domains. Numerous real-world applications, including astronomy and economics, depend on the ability to comprehend and use big numbers. Here are some real-world applications for big numbers:
Examples of Large NumbersHere are a few solved examples for you curators to better understand the topic: Example 1: Add 789,456,123 and 987,654,321.  Example 1 Example 2: Subtract 123,456,789 from 987,654,321.  Example 2 Example 3: Multiply 133,556 by 749.  Example 3 Example 4: 2750490 by 122. 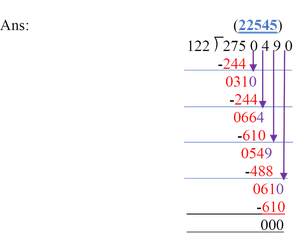 Example 4 Division Illustration:Practice Problem of Large NumbersQ1. With which place does a 7-digit number start in the Indian system?
Q2. Find the sum of the greatest 8-digit number and the smallest 9−digit number. Q3. Write numerals for the following:
FAQs on Large NumbersWhat are Large Numbers?
How are Large Numbers Represented?
What is the Difference Between American and British Systems of Naming Large Numbers?
What are Some Common Large Numbers we Encounter in Daily Life?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
Reffered: https://www.geeksforgeeks.org
| Mathematics |
Type: | Geek |
Category: | Coding |
Sub Category: | Tutorial |
Uploaded by: | Admin |
Views: | 23 |