Calculating the distance of a point from a line is a fundamental concept in geometry with numerous applications in fields like computer graphics, navigation, and even machine learning.

In this article, we have covered, Distance of a Point from a line definition, its formula in 2D and 3D and others in detail.

What is Distance of a Point From a Line?

Distance between a point and a line (in a 2D or 3D space) is the distance of a perpendicular line drawn from a point to the line. This perpendicular distance from a point to a line is also the shortest distance between them.

Formula for Distance of a Point From a Line in 2D

The perpendicular distance from a point P(x₁, y₁) and line A.x + B.y + C = 0 in 2D space is given by,

d = | A.x₁ + B.y₁ + C | / (A² + B²)^1/2

Where,

• d is Distance (shortest) between point(x₁, y₁)
• A, B are Coefficients of x and y coordinates respectively, in General Equation of Line
• C is Constant in General Equation of Line

Formula for Distance of a Point From a Line in 3D

The perpendicular distance between a point P(x₁, y₁, z₁) and a line with distance vector [Tex]\overrightarrow{\rm v}[/Tex], is given by,

[Tex]D = |\overrightarrow{\rm AP}×\overrightarrow{\rm v}| / |\overrightarrow{\rm v}|[/Tex]

Where,

• D is Perpendicular Distance from point P and line given by vector direction [Tex]\overrightarrow{\rm v}[/Tex]
• A is a Point on Line with Distance Vector [Tex]\overrightarrow{\rm v}[/Tex]
• [Tex]\overrightarrow{\rm AP}[/Tex] is Distance Vector of Line that Passes through point A and P

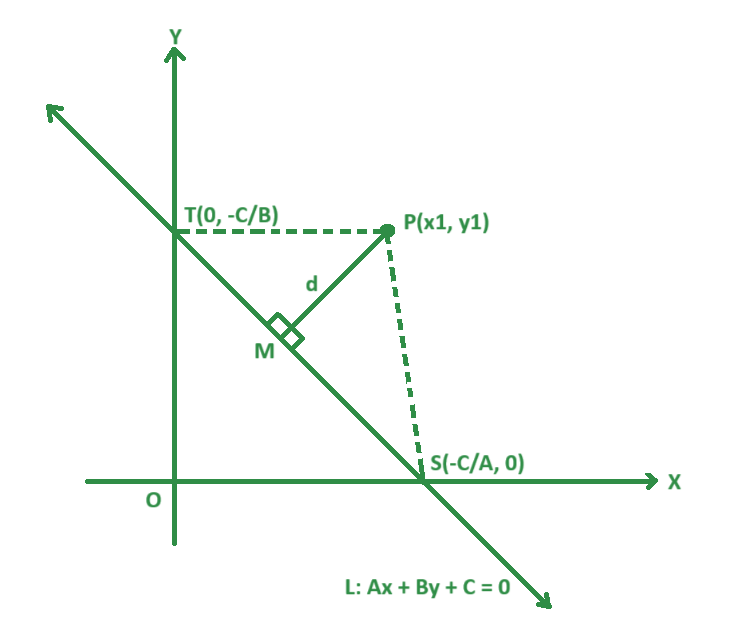
Perpendicular Distance of a Point From a Line

As defined above, the distance, (shortest distance) of a point from a line, is the length of the perpendicular drawn from the point to the line. Below are the steps to derive the formula for finding the shortest distance between a point and a line.

Step 1: Consider a line (L: Ax + By + C = 0) whose distance from the point {P (x₁, y₁)} is (d).

Step 2: Draw a perpendicular (PM) from the point (P) to the line (L) as shown in the figure below.

Step 3: Let (Q) and (R) be the points where the line meets the x-axis and y-axis, respectively.

Step 4: Coordinates of the points can be written as Q(-C/A, 0) and R(0, -C/B).

Now using the formula one can easily found the distance of the point from the line.

Derivation of Distance of a Point from a Line in 2D

Let’s consider a point P(x₁, y₁) and a line L: Ax + By + C = 0 passing through and intersecting the x-axis and y-axis at points S and T. Then, the coordinates of S and T are given by S(-C / A, 0) and T (0, -C / B). Also, consider the perpendicular line PM from P to the line segment S and T as d.

Derivation of Distance of a Point from a Line in 2D

We know that,

Area of Triangle PST = 1/2(PM × ST)

2 × area of triangle PST = PM × ST—- equation(i)

Area of triangle PST = (1/2) × ((x₁.(0 + (C/B))) + (-C/A)((-C/B) – y₁)+ 0(y₁ – 0))

= (1/2) × |x₁.(C/B) + y₁(C/A) + (C²/ AB)|

Or, 2 × area of triangle PST = |x₁(C/B) + y₁(C/A) + (C²/ AB)|—- equation(ii)

By Distance formula,

ST = ((0 + (C/A))² + ((C/B) – 0)²)^1/2

ST = |C/AB| (A² + B²)^1/2—- equation(iii)

By putting the value of equation (ii) and equation (iii) in equation (i), we get,

|x₁(C/B) + y₁(C/A) + (C²/ AB)| = PM × |C/AB| (A² + B²)^1/2

PM = (|C/AB| | A.x₁ + B.y₁ + C |) / (|C/AB| (A² + B²)^1/2)

PM = |A.x₁ + B.y₁ + C| / (A² + B²)^1/2

Therefore, the shortest perpendicular distance from a point to a line is,

d= | A.x₁ + B.y₁ + C | / (A² + B²)^1/2

Derivation of Distance of a Point from a Line in 3D

Let’s consider a line L in 3D space passing through a point A with direction vector [Tex]\overrightarrow{\rm v}[/Tex]. So, A is any point on the line with distance vector[Tex]\overrightarrow{\rm v}[/Tex]. Let P be any point which is not the line L.

Derivation of Distance of a Point from a Line in 3D

In the diagram given above, we have a vector passing through point P which is parallel to the line with distance vector [Tex]\overrightarrow{\rm v}[/Tex] and also, we have a line parallel to line AP with distance vector [Tex]\overrightarrow{\rm AP}[/Tex].

By applying parallelogram law, with the help of given line L with distance vector [Tex]\overrightarrow{\rm v}[/Tex] and line passing through point A and P with distance vector [Tex]\overrightarrow{\rm AP}[/Tex],

Now, we find the area of parallelogram in two ways,

Way 1 (Finding Area of Parallelogram)

By the geometric interpretation of the magnitude of cross product,

Area of parallelogram = Magnitude of the cross product between vectors [Tex]\overrightarrow{\rm v}[/Tex] and [Tex]\overrightarrow{\rm AP}[/Tex]

⇒ Area of Parallelogram = | [Tex]\overrightarrow{\rm AP}[/Tex] × [Tex]\overrightarrow{\rm v}[/Tex]|—–> equation(i)

Way 2 (Finding Area of Parallelogram)

We can also find area of parallelogram by multiplying base of the parallelogram with its altitude or height,

Area of Parallelogram = Magnitude of vector [Tex]\overrightarrow{\rm v}[/Tex] × D

⇒ Area of Parallelogram = |[Tex]\overrightarrow{\rm v}[/Tex]| × D—–> equation(ii)

From equations, (i) and (ii), we get,

|[Tex]\overrightarrow{\rm v}[/Tex]| × D = | [Tex]\overrightarrow{\rm AP}[/Tex] × [Tex]\overrightarrow{\rm v}[/Tex]|

D = |[Tex] \overrightarrow{\rm AP}[/Tex] × [Tex]\overrightarrow{\rm v}[/Tex] | / | [Tex]\overrightarrow{\rm v}[/Tex]|

Therefore the shortest perpendicular distance, D from point P(x1, y1, z1) to a line L, is given by,

D = | [Tex]\overrightarrow{\rm AP} [/Tex]× [Tex]\overrightarrow{\rm v}[/Tex] | / | [Tex]\overrightarrow{\rm v}[/Tex] |

Conclusion

Calculating the distance of a point from a line might seem complex initially, but with the formula and step-by-step method explained here, it becomes a straightforward task. This fundamental geometric concept is not only important for academic purposes but also has significant real-world applications, making it a valuable tool in your mathematical toolkit.

Examples on Distance of a Point From a Line

Example 1: Find the distance of point(2, -4) from the line 2x – 6y – 24 = 0

Solution:

Let the point(x₁, y₁) = (2, -4)

Given line is 2x – 6y – 24 = 0, comparing it with the general equation of line, Ax + By + C = 0, we get,

A = 1, B = -6 and C = -24

Now, the distance of point (2, -4) from the line 2x – 6y – 24 = 0 is given by,

d= |A.x₁ + B.y₁ + C | / (A² + B²)^1/2

d = |1(2) + (-6)(-4) + (-24)| / (1² + (-6)²)^1/2

d = |2 + 24 – 24| / (1 + 36)^1/2

d = 2/√(37)

Therefore, the distance from point(2, -4) and line 2x – 6y – 24 = 0 is, 2/√(37) unit.

Example 2: Find the distance between line 3x – 4y + 10 = 0 and point (-2, 6)

Solution:

According to the question,

Let, point(x₁, y₁) = (-2, 6)

Comparing the given line is 3x – 4y + 10 = 0, with the general equation of line, Ax + By + C = 0, we get,

A = 3, B = -4 and C = 10

Now, the distance of point (-2, 6) from the line 3x – 4y + 10 = 0 is given by,

d= |A.x₁ + B.y₁ + C | / (A² + B²)^1/2

d = | 3(-2) + (-4)(6) + 10 | / (3² + (-4)²)^1/2

d = | (-6) – 24 + 10| / (9 + 16)^1/2

d = 20/5

d = 4

Therefore, the distance from point(-2, 6) and line 3x – 4y + 10 = 0 is, 4 unit.

Example 3: Find the shortest distance from point(3 , 4) to 2x + 3y – 5 = 0

Solution:

According to the question,

Let, point(x₁, y₁) = (3, 4)

Comparing the given line is 2x + 3y – 5 = 0, with the general equation of line, Ax + By + C = 0, we get,

A = 2, B = 3 and C = -5

The shortest distance from point(3, 4) to 2x + 3y – 5 = 0 is given by,

d = | A.x₁ + B.y₁ + C | / (A² + B²)^1/2

d = | 2(3) + 3(4) + (-5) | / (2² + 3²)^1/2

d = | 6 + 12 – 5| / (4 + 9)^1/2

d = 13 / 13^1/2

d = √(13)

Therefore, the shortest distance from point(3, 4) to 2x + 3y – 5 = 0 is √(13) unit.

Example 4: Find the distance from the point(6, 6) passing through points(3, 0) and (0, 4).

Solution:

We are given, point(x₁, y₁) = (6, 6)

We can find the equation of line passing through points(3, 0) and (0, 4) with the help of distance formula,

Equation of line is given by,

y – y₁ = m(x – x₁) —– equation(i)

From point(3, 0), let y₁ = 0, x₁ = 3,

Slope, m = (4 – 0)/(0 – 3) = (-4)/3

Putting the above obtained values in equation(i), we get,

y – 0 = (-4)/3 (x – 3)

3y = -(4x)/3 + 4

4x/3 + 3y – 4 = 0

4x + 9y – 12 = 0

Now, the distance from point(6, 6) to the line 4x + 9y – 12 = 0 is given by,

By observation, x₁ = 6, y₁ = 6, A = 4, B = 9 and C = -12

So, d = | A.x₁ + B.y₁ + C | / (A² + B²)^1/2

d = | 4(6) + 9(6) – 12 | / (4² + 9²)^1/2

d = | 24 + 54 – 12 | / (16 + 36)^1/2

d = 66 / √(52)

Therefore, the distance from point(6, 6) and line passing through points(3, 0) and (0, 4) is 66 / √(52) unit.

Example 5: Find the perpendicular distance from point(5, 6) to the line x = -3.

Solution:

Given, point(x₁, y₁) = (5, 6)

Equation of line, x = -3, can be written as, x + 3 = 0. Comparing it with the general equation of line Ax + By + C = 0, we get,

A = 1, B = 0, C = 3

Now, the perpendicular distance from point(5, 6) to the line x + 3 = 0 is given by,

d = | A.x₁ + B.y₁ + C | / (A² + B²)^1/2

d = |1(5) + 0(6) + 3 | / (1² + 0²)^1/2

d = 14/1

d = 14

Therefore, the perpendicular distance from point(5, 6) to the line x = -3 is 14 unit.

Example 6: Find the distance between the point P(0, 3, 6) and the line with parameters equations x = 1 – t, y = 1 + 2t, z = 5 + 3t.

Solution:

Given Point P(0 , 3, 6) and line with parametric equations, x = 1 – t, y = 1 + 2t, z = 5 + 3t

[Tex]\overrightarrow{\rm v}[/Tex] = ( -1, 2, 3)

Let the point on line, A = (1, 1, 5) from the parametric equation of line.

So, [Tex]\overrightarrow{\rm AP}[/Tex] = Difference between points P and A

⇒ [Tex] \overrightarrow{\rm AP} [/Tex]= (0, 3, 6) – (1, 1, 5)

⇒ [Tex] \overrightarrow{\rm AP} [/Tex]= (-1, 2, 1)

Now, [Tex] \overrightarrow{\rm AP} [/Tex]× [Tex] \overrightarrow{\rm v} [/Tex]= [Tex]\begin{vmatrix} \overrightarrow{\rm i} & \overrightarrow{\rm j} & \overrightarrow{\rm k} \\ -1&2 & 1 \\ -1&2 & 3 \end{vmatrix}[/Tex]

=(6 – 2) [Tex] \overrightarrow{\rm i } [/Tex]– (-3 + 1)[Tex] \overrightarrow{\rm j} [/Tex]+ (-2 – (-2))[Tex] \overrightarrow{\rm k} [/Tex]

= 4[Tex] \overrightarrow{\rm i } [/Tex]+2[Tex] \overrightarrow{\rm j} [/Tex]+ 0[Tex] \overrightarrow{\rm k} [/Tex]

By distance formula,

D = |[Tex] \overrightarrow{\rm AP}[/Tex] X [Tex]\overrightarrow{\rm v}[/Tex] | / | [Tex]\overrightarrow{\rm v}[/Tex] |

D = (4² + 2² + 0²)^1/2 / ((-1)² + 2² + 3²)^1/2

D = √(70) / 7

Therefore, the distance from point P(0, 3, 6) to the line with parametric equations, x = 1 – t, y = 1 + 2t, z = 5 + 3t is √(70) / 7 unit.

Problem 7: Let L be a line passing through point A(6, 4, 4) in direction vector(1, 3, -10). Find the distance from point P(1, 5, 5) to the line L.

Solution 7:

Given point P(1, 5, 5) and line L passing through point A(6, 4, 4) in [Tex]\overrightarrow{\rm v}[/Tex] = (1, 3, -10)

[Tex]\overrightarrow{\rm AP}[/Tex] = (1 , 5, 5) – (6, 4, 4)

⇒ [Tex]\overrightarrow{\rm AP} [/Tex]= (-5, 1, 1)

Now, [Tex]\overrightarrow{\rm AP}[/Tex] ×[Tex]\overrightarrow{\rm v} [/Tex]= [Tex]\begin{vmatrix} \overrightarrow{\rm i} & \overrightarrow{\rm j} & \overrightarrow{\rm k} \\ -5&1 & 1 \\ 1&3 & -10 \end{vmatrix}[/Tex]

=(-10 -3)[Tex]\overrightarrow{\rm i}[/Tex] – (50 – 1)[Tex]\overrightarrow{\rm j}[/Tex] + (-15 – 1)[Tex]\overrightarrow{\rm k}[/Tex]

= -13[Tex]\overrightarrow{\rm i}[/Tex] -49[Tex]\overrightarrow{\rm j}[/Tex] + 14[Tex]\overrightarrow{\rm k}[/Tex]

By distance formula,

D = | [Tex]\overrightarrow{\rm AP}[/Tex] × [Tex]\overrightarrow{\rm v}[/Tex] | / | [Tex]\overrightarrow{\rm v} [/Tex]|

D = ((-13)² + (49)² + 14²)^1/2 / (1² + 3² + (-10)²)^1/2

D = (2766)^1/2 / (110)^1/2

D = (25.14545)^1/2

D = 5.014 (approx.)

Therefore, 5.014 unit (approx.) is the distance from point (1, 5, 5) to the line passing through (6, 4, 4) in direction vector (1, 3, -10).

FAQs on Distance of a Point From a Line

How to Find Distance from a Point to Line in 2D?

We can find distance from a point p(x₁, y₁) to the line Ax + By + C = 0, by formula,

Distance, d = | A.x₁ + B.y₁ + C | / (A² + B²)^1/2

What are Real-World Applications of Finding the Shortest Distance from a Point to Line?

Formula for finding the distance between a point to a line is very crucial in various fields, such as in navigation systems for calculating the proximity of the location of users to roads, in computer graphics for detecting collisions, in computer algorithms for optimization and minimizing the function errors, and much more.

What does Distance Formula From a Point to a Line Measure?

The distance formula from a point to the line measures the shortest distance as the perpendicular distance from a given point to a given line.

Can we Extend Distance Formula from a Point to a line in 3D space?

Yes, we can extend this distance formula in 3D space, but the distance formula would be different.

What happens to Distance between a Point and a Line when the Point lies on the Same Line?

In such a case, the distance between the given point and the given line becomes zero.

Is it Possible that the Distance between a line and a point 3D space be zero?

Yes, it is possible when the point is on the line in 3D space.