Horje
Largest Sum Contiguous Subarray in C

In this article, we will learn how to find the maximum sum of a contiguous subarray for a given array that contains both positive and negative integers in C language.

Example:

Input: 
arr = {-2, -3, 4, -1, -2, 1, 5, -3}

Output: 
7

Explanation: The subarray {4,-1, -2, 1, 5} has the largest sum 7.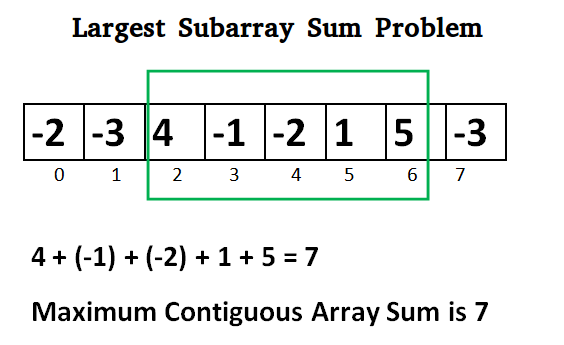
kadane-Algorithm_img

Maximum subarray Sum

Table of Content

Method 1: Traversing Over Every Subarray

In this method, we traverse over every contiguous subarray, calculate the sum of each subarray, and return the maximum sum among them.

Approach:

  • Run a nested loop to generate every subarray.
  • Calculate the sum of elements in the current subarray.
  • Return the maximum sum from these subarrays.

Below is the implementation of the above approach:

C 
// C program to find Maximum Subarray Sum
#include <stdio.h>

// Find maximum between two numbers.
int max(int num1, int num2)
{
    return (num1 > num2) ? num1 : num2;
}

// Returns the sum of max sum subarray
int maxSubarraySum(int arr[], int n)
{
    // Initializing result
    int result = arr[0];

    for (int i = 0; i < n; i++) {
        int sum = arr[i];
        // traversing in current subarray
        for (int j = i + 1; j < n; j++) {
            // updating result every time
            // to keep an eye over the maximum sum
            result = max(result, sum);
            sum += arr[j];
        }
        // updating the result for (n-1)th index.
        result = max(result, sum);
    }
    return result;
}

int main()
{
    // initialize an array
    int arr[] = { -2, 1, -3, 4, -1, 2, 1, -5, 4 };
    // calculate the size of an array
    int n = sizeof(arr) / sizeof(arr[0]);
    // print the maximum sum of subarray
    printf("Maximum Subarray Sum is %d\n",
           maxSubarraySum(arr, n));
    return 0;
}

Output
Maximum Subarray Sum is 6

Time Complexity: O(N^2)
Auxiliary Space: O(1)

Method 2: Using Kadane’s Algorithm

Kadane’s Algorithm is an efficient way to find the maximum subarray sum with a linear time complexity.

Maximum-Sum-Subarray-(-Kadane's-Algorithm)-(2)

Illustration of Kadane’s Algorithm

Approach:

  • Initialize two variables: max_so_far and max_ending_here.
  • Iterate through the array and update these variables as follows:
    • max_ending_here = max(arr[i], max_ending_here + arr[i])
    • max_so_far = max(max_so_far, max_ending_here)
  • Return max_so_far as the result.

Below is the implementation of the above approach:

C 
// C program to solve maximum subarray sum problem using
// Kadane’s Algorithm
#include <stdio.h>

// Function to return maximum of two integers
int max(int a, int b) { return (a > b) ? a : b; }

// Function to find the maximum sum subarray
int maxSubarraySum(int arr[], int n)
{
    int max_so_far = arr[0];
    int max_ending_here = arr[0];

    for (int i = 1; i < n; i++) {
        max_ending_here
            = max(arr[i], max_ending_here + arr[i]);
        max_so_far = max(max_so_far, max_ending_here);
    }
    return max_so_far;
}

int main()
{
    // Initialize the array
    int arr[] = { -2, 1, -3, 4, -1, 2, 1, -5, 4 };
    // Calculate the number of elements in the array
    int n = sizeof(arr) / sizeof(arr[0]);

    // Print the maximum sum of any subarray
    printf("Maximum Subarray Sum is %d\n",
           maxSubarraySum(arr, n));

    return 0;
}

Output
Maximum Subarray Sum is 6

Time Complexity: O(N)
Auxiliary Space: O(1)

Method 3: Using Dynamic Programming

We can use the dynamic programming approach to solve this problem by using an auxiliary array to store the maximum subarray sum ending at each position.

Approach:

  • Create an auxiliary array dp of the same size as the input array.
  • Initialize dp[0] with arr[0].
  • Iterate through the array starting from the second element:
    • dp[i] = max(arr[i], dp[i – 1] + arr[i])
  • The maximum value in the dp array will be the maximum subarray sum.

Below is the implementation of the Dynamic Programming approach in C:

C 
// C program to solve maximum subarray sum problem using
// Dynamic Programming
#include <stdio.h>

// Function to return maximum of two integers
int max(int a, int b) { return (a > b) ? a : b; }

// Function to find the maximum sum subarray using Dynamic
// Programming
int maxSubarraySumDP(int arr[], int n)
{
    int dp[n];
    dp[0] = arr[0];

    int max_so_far = dp[0];

    for (int i = 1; i < n; i++) {
        dp[i] = max(arr[i], dp[i - 1] + arr[i]);
        max_so_far = max(max_so_far, dp[i]);
    }
    return max_so_far;
}

int main()
{
    // Initialize the array
    int arr[] = { -2, 1, -3, 4, -1, 2, 1, -5, 4 };
    // Calculate the number of elements in the array
    int n = sizeof(arr) / sizeof(arr[0]);

    // Print the maximum sum of any subarray
    printf("Maximum Subarray Sum is %d\n",
           maxSubarraySumDP(arr, n));

    return 0;
}

Output
Maximum Subarray Sum is 6

Time Complexity: O(N)
Auxiliary Space: O(N)

Both Kadane’s Algorithm and the Dynamic Programming approach provide efficient solutions to the Maximum Subarray Sum problem. Kadane’s Algorithm is generally preferred due to its lower auxiliary space complexity.


 


Reffered: https://www.geeksforgeeks.org

C Language

Related
C Program to Implement Circular Linked List C Program to Implement Circular Linked List
Queue using Linked List in C Queue using Linked List in C
Tarjan’s Algorithm in C Language Tarjan’s Algorithm in C Language
N Queen Problem Using Branch and Bound in C N Queen Problem Using Branch and Bound in C
Partition Equal Subset Sum in C Partition Equal Subset Sum in C

Type:
 Geek
Category:
 Coding
Sub Category:
 Tutorial
Uploaded by:
 Admin
Views:
 18



 

Horje