|
|
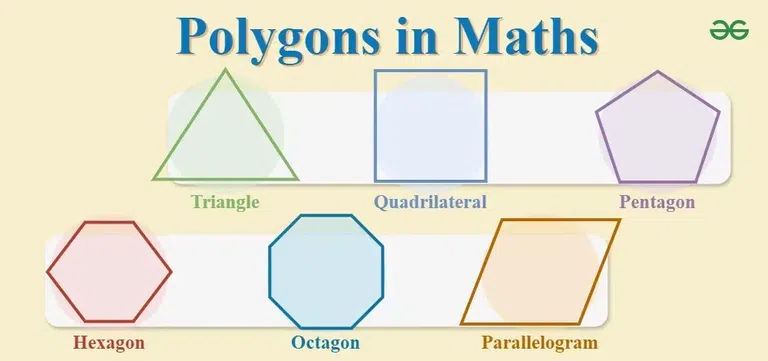
In mathematics, practice questions are extremely important for understanding any concept or theory. Especially when it comes to study a branch like Geometry or Mensuration, the solving of practice questions not only helps in understanding these topics but also increases the accuracy of solving them for of the students. Topics such as Polygon, Types of Polygon, Polygon Formula etc. are of great importance for school mathematics as well as for many competitive exams like SSC CGL, SSC MTS, Railway, State PCS, Banking etc. In this article we will discuss about Polygon, it’s formulas, solved and unsolved practice questions in detail. What is Polygon ?Polygons are two dimensional figures , formed by three or more line segments and they are fully enclosed in shape. Polygons are formed by straight sides or lines not by curves. Since there are more than two line segments, a polygon has a vertex. A vertex is a point that is formed at the junction of two line segments. Polygons are made of various numbers of sides and their names indicate how many sides those polygons have. For example, a triangle has three sides, a quadrilateral has four sides. 
Formulas of PolygonSome important formulas of angles in a polygon:
There are various number of formulas related to polygons in geometry. These formulas are based on various matter such as,
Area of PolygonsThe area based formulas of various polygons are given below:
Perimeter of PolygonsThe perimeter based formulas are given below:
Diagonals of PolygonFormula for number of diagonal of polygon is given as:
Solved Practice Problems on PolygonsProblem 1: A convex polygon has 20 diagonals. Find the number of sides of that polygon. Solution:
Problem 2: Find the number of sides of a polygon whose sum of all interior angle is 2160°. Solution:
Problem 3: If the external angle of a polygon is 45°, then find the number of diagonal in this polygon. Solution:
Problem 4: Find the measure of each angle of a regular nonagon. Solution:
Problem 5: If the area of a trapezium is 200 cm2 and the measures of parallel sides are 6 cm and 4 cm, respectively, then find the height of the trapezium. Solution:
Problem 6: Find each interior angle of a regular polygon of 15 sides. Solution:
Problem 7: A parallelogram has 25 cm of length and width is 30 cm. Find out the perimeter of the given parallelogram. Solution:
Problem 8: Find the area of a right angle triangle with base = 9 cm and hypotenuse = 15 cm. Solution:
Problem 9: Find out the area of a rhombus having diagonals equal to 5 cm and 6 cm. Solution:
Problem 10: If the sides of a pentagon are 3cm, 3.5cm, 4cm, 5cm and 6cm , then find out the perimeter of the pentagon. Solution:
Practice Questions on PolygonsQ1: One angle of a hexagon is 90° and all the remaining five angles are equal. Then find out the measure of the other angle. Q2: Find the sum of all the interior angles having 16 sides . Q3: The perimeter of a rectangle is 120 cm, and the width is 10 cm. What is the length of this rectangle? . Q4: The sum of all the interior angles of a polygon is 1440° Q5: The length and width of a rectangle are 15 cm and 25 cm, respectively. What is the perimeter of this rectangle?. Q6: The number of sides of a regular polygon is 24, what is the interior angle of the polygon ? Q7: Find the area and perimeter of a regular pentagon whose side is 5 cm and apothem length is 6 cm. ?? Q8: One of the internal angle of a regular polygon is 135°. Find the number of sides in the polygon. Q9: Find the area of a rhombus in which the diagonal lengths are 10 cm and 8 cm respectively. Also Check,
FAQs on PolygonsWhat is a 7 sided polygon called?
What is called smallest polygon?
What is a 100-sided polygon called?
What are the first 7 polygons?
What are Properties of a Polygon?
Can a Circle be Classified as a Polygon?
|
||||||||||||||||||||||||||||||||||||||||
Reffered: https://www.geeksforgeeks.org
| Mathematics |
| Related |
|---|
| |
| |
| |
| |
| |
Type: | Geek |
Category: | Coding |
Sub Category: | Tutorial |
Uploaded by: | Admin |
Views: | 17 |