Kernel ridge regression (KRR) is a powerful technique in scikit-learn for tackling regression problems, particularly when dealing with non-linear relationships between features and the target variable.  This technique allows for the modeling of complex, nonlinear relationships between variables, making it a valuable asset in data analysis.

This article delves into the inner workings of KRR, exploring its theoretical foundations, implementation details in scikit-learn, and practical considerations for effective use.

Understanding Kernel Ridge Regression

Kernel ridge regression is a variant of ridge regression that uses the kernel trick to learn a linear function in a high-dimensional feature space. This allows KRR to handle nonlinear data without the need for explicit transformation into a higher-dimensional space. The kernel trick is a mathematical technique that enables the computation of dot products in the high-dimensional feature space without explicitly mapping the data into that space. This is achieved by using a kernel function, which computes the dot product between two vectors in the high-dimensional space based on their original feature space representations.

Key Components of Kernel Ridge Regression:

1. Kernel Functions: Kernel functions are the core of KRR. They define the similarity between data points in the high-dimensional feature space. Common kernel functions include the radial basis function (RBF), polynomial kernel, and sigmoid kernel. Each kernel function has its own strengths and weaknesses, and the choice of kernel depends on the specific problem and data characteristics.
2. Regularization: Regularization is a crucial aspect of KRR. It helps prevent overfitting by adding a penalty term to the loss function. The regularization strength is controlled by the alpha parameter, which determines the magnitude of the penalty.
3. Dual Coefficients: In KRR, the weights are not computed directly. Instead, the dual coefficients are calculated, which are the weights in the high-dimensional feature space. These coefficients are used to make predictions.

Implementing Kernel Ridge Regression with Scikit-Learn

Scikit-Learn provides an efficient implementation of KRR through the KernelRidge class. This class allows for easy creation and training of KRR models. The constructor of the KernelRidge class accepts several parameters, including the kernel function, regularization strength (alpha), and kernel parameters (e.g., gamma for RBF kernel).

Steps to Implement Kernel Ridge Regression:

• Import Libraries: Start by loading the required libraries, these are from sklearn and other related libraries.
• Load Dataset: Open the dataset you are going to use for solving the problem. Some of the datasets that are provided by Scikit-Learn for practice includes the following.
• Preprocess Data: Before applying the logistic regression model, pre-Process your data; partitioning the data into training set and test set then normalize the independent variables.
• Initialize KRR Model: Instantiate an object of Kernel Ridge Regression from sklearn.
• Fit Model: This simply involves feeding the model to the training data available.
• Make Predictions: From trained model, make predictions of the responses of the independent variables with respective to the dependent ones in the test data.
• Evaluate Model: Evaluate the model using the correct measures that include Mean Squared Error (MSE).

Let’s walk through an example using a synthetic dataset.

Step 1: Import Libraries:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.kernel_ridge import KernelRidge
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error

Step 2: Load Dataset:

X, y = make_regression(n_samples=100, n_features=1, noise=0.1)

Step 3: Preprocess Data:

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

Step 4: Initialize KRR Model:

krr = KernelRidge(kernel='rbf', alpha=1.0, gamma=0.1)

Step 5: Fit Model:

krr.fit(X_train, y_train)

Step 6: Make Predictions:

y_pred = krr.predict(X_test)

Step 7: Evaluate Model

mse = mean_squared_error(y_test, y_pred)
print(f'Mean Squared Error: {mse}')

Output:

Mean Squared Error: 102.02879465229866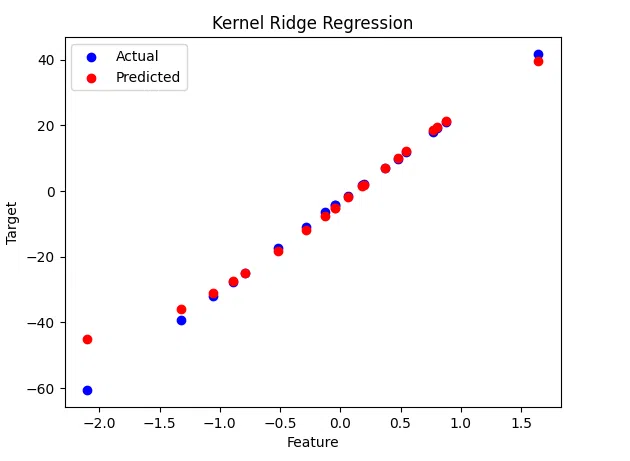

Kernel Ridge Regression

Example: Predicting a Sinusoidal Function Using Kernel Ridge Regression

Let’s walk through an example of using Kernel Ridge Regression to predict a sinusoidal function.

import numpy as np
from sklearn.kernel_ridge import KernelRidge
import matplotlib.pyplot as plt

rng = np.random.RandomState(42)
X = 5 * rng.rand(100, 1)
y = np.sin(X).ravel()
y[::5] += 3 * (0.5 - rng.rand(X.shape[0] // 5))

model = KernelRidge(alpha=1.0, kernel='rbf', gamma=0.1)
model.fit(X, y)
X_plot = np.linspace(0, 5, 1000)[:, None]
y_plot = model.predict(X_plot)
plt.scatter(X, y, color='black', label='Data')
plt.plot(X_plot, y_plot, color='red', label='KRR Prediction')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title('Kernel Ridge Regression with RBF Kernel')
plt.show()

Output:

Kernel Ridge Regression

Example: Kernel Ridge Regression with Laplacian Kernel on Moon-shaped Data

Let’s demonstrate Kernel Ridge Regression, this time using a different dataset and the Laplacian kernel.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.kernel_ridge import KernelRidge
from sklearn.datasets import make_moons

X, y = make_moons(n_samples=100, noise=0.1, random_state=42)
model = KernelRidge(alpha=0.1, kernel='laplacian', gamma=0.1)
model.fit(X, y)

x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.figure(figsize=(8, 6))
plt.contourf(xx, yy, Z, cmap=plt.cm.RdBu, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.RdBu, edgecolors='k')
plt.title('Kernel Ridge Regression with Laplacian Kernel')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.colorbar()
plt.show()

Output:

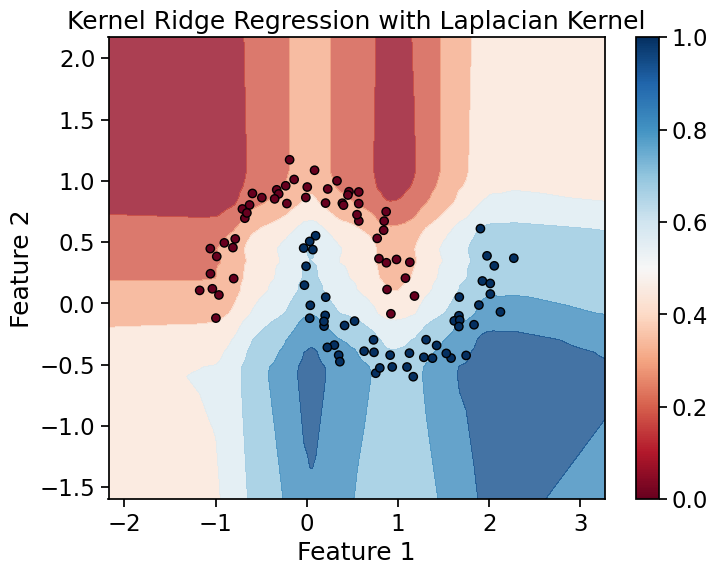Kernel Ridge Regression with Laplacian Kernel

Utilizing Kernel Ridge Regression : Practical Considerations

• Handling Large Datasets: Kernel Ridge Regression can be computationally expensive for large datasets due to the need to compute the kernel matrix. Techniques such as the Nyström method or random Fourier features can be used to approximate the kernel matrix and reduce computational complexity.
• Regularization: Regularization is essential to prevent overfitting, especially when using complex kernels. The regularization parameter alpha controls the trade-off between fitting the training data and keeping the model weights small.
• Kernel Selection: The choice of kernel significantly impacts the performance of the model. Experimenting with different kernels and their parameters is crucial to finding the best model for a given dataset.

Conclusion

Kernel Ridge Regression is a versatile and powerful regression technique that leverages the kernel trick to handle non-linear data. By combining the strengths of Ridge Regression and kernel methods, KRR provides a robust solution for complex regression tasks. With Scikit-Learn, implementing and tuning KRR models is straightforward, making it an excellent tool for data scientists and machine learning practitioners.

Kernel ridge regression- FAQs

How does Kernel Ridge Regression differ from Ridge Regression?

Kernel Ridge Regression is an extension of Ridge Regression, with one difference that while Ridge Regression is a linear model it decreases the model coefficient to avoid overfitting, Kernel Ridge Regression uses the kernel functions. They allow the model to learn non-linear relationships because by construction the model operates in higher-dimensional space.

What are kernel functions?

Kernel functions are mathematical functions that forms the basis of KRR where the error is minimized in a transformed high dimension space. Some of the kernel functions are linear kernel, polynomial kernel and the radial basis function kernel (RBF).

Why use Kernel Ridge Regression?

Kernel Ridge Regression is of great help when the nature of relationship between the independent and dependent variables present in your data is highly non linear. It integrates the strict structure of the Ridge Regression model with the expressive function of the kernel methods, thus it is one of the most effective tools for pattern capturing.

How do you choose the right kernel for Kernel Ridge Regression?

Kernel Ridge Regression is used when one has to predict higher order polynomial regression in the given data. It features the robustness of Ridge Regression in regularizing the variables while including the adaptability of the kernel methods to capture complex trends.