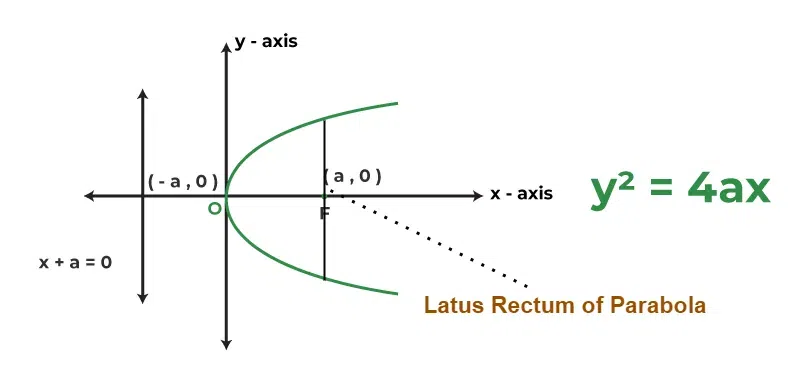
Latus rectum is a crucial concept in the study of conic sections, such as parabolas, ellipses, and hyperbolas. The name latus rectum comes from the Latin words “latus” means (side) and “rectum” means (straight). It refers to the line segment perpendicular to the major axis of the conic section that passes through the focus of the conic section and has endpoints on the curve.

Understanding the latus rectum is essential for analyzing the geometric properties and dimensions of these curves. Latus Rectum plays a significant role in defining the geometric effects of conic sections like ellipses, parabolas, and hyperbolas.

This article provides a detailed explanation of the latus rectum, highlighting its relationship to the focal points and axes of conic sections

What is Latus Rectum?

Latus rectum of a conic section is a line segment that passes through a focus of the conic section and is perpendicular to the major axis. Its endpoints lie on the curve of the conic section. The length of the latus rectum is a measure of how “wide” the conic section is at the focus. It plays a significant role in characterizing the geometric properties of conic sections like ellipses, parabolas, and hyperbolas.

Terms Related to Latus Rectum

These are various terms required to define the Latus Rectum are:

Directrix

Directrix of a conic section is a line such that the ratio of the distance of any point on the conic from the focus to its perpendicular distance from the directrix is constant. This ratio is known as the eccentricity ????.

Transverse Axis

Transverse axis is a term used specifically in the context of hyperbolas. The transverse axis of a hyperbola is the line segment that joins the two vertices of the hyperbola and passes via the center. It is the axis along which the hyperbola opens, and it fibs along the line that intersects the foci of the hyperbola.

Conjugate Axis

Conjugate axis is a term associated with hyperbolas, completing the concept of the transverse axis. It plays a significant role in defining the structure and properties of hyperbolas. The conjugate axis of a hyperbola is the line segment that is perpendicular to the transverse axis and passes through the center of the hyperbola. It does not intersect the hyperbola itself but helps in describing its asymptotic behavior and the form of the associated rectangle used in drawing the hyperbola.

Latus Rectum of Parabola

The latus rectum is the line segment that passes through the focus, perpendicular to the axis of symmetry of the parabola. The length of the latus rectum for a standard equation of a parabola y² = 4ax is equal to LL’ = 4a. The endpoints of the latus rectum of a Parabola are (a, 2a), (a, -2a).

Latus Rectum of Parabola

Length = 4a

a=  parabola’s focal length.

Properties of Latus Rectum a Parabola

• Symmetry: Latus rectum is symmetric with respect to the axis of the parabola.
• Focus: It passes through the focus of the parabola.
• Length: Length of the latus rectum is always four times the distance from the vertex to the focus.

Latus Rectum of Hyperbola

The latus rectum of a hyperbola is the line segment that passes through one of the foci and is perpendicular to the transverse axis and whose ending point lies on the hyperbola. The length of the latus rectum is given by [Tex]2b^2/a[/Tex]​, similar to the ellipse, where a and b are the lengths of the semi-transverse and semi-conjugate axes, respectively.

Latus Rectum of Hyperbola

Length = [Tex]2b^2/a[/Tex]

a= length of semi transverse axis

b= length of semi conjugate axis

Properties of Latus Rectum of a Hyperbola

• Focus: Latus rectum passes through each focus of the hyperbola.
• Length: Length of each latus rectum is proportional to the square of the semi-minor axis divided by the semi-major axis, similar to an ellipse.
• Endpoints: Endpoints can be found by substituting the x-coordinate of the focus into the hyperbola’s equation to find the corresponding y-coordinates.

Latus Rectum of a Ellipse

Latus rectum of an ellipse is a line segment that is perpendicular to the major axis and passes through either focus, and whose endpoints lie on the ellipse. The length of the latus rectum is given by [Tex]2b^2/a[/Tex]​, where a is the length of the semi-major axis and b is the length of the semi-minor axis. It is an important geometric feature used in various calculations and properties of ellipses.

Length = [Tex]2b^2/a[/Tex]

a= length of semi-major Axis

b= Length of semi minor axis

Properties of Latus Rectum of an Ellipse

• Focus: Latus rectum passes through each focus of the ellipse.
• Length: Length of each latus rectum is proportional to the square of the semi-minor axis divided by the semi-major axis.
• Endpoints: Endpoints can be found by substituting the x-coordinate of the focus into the ellipse’s equation to find the corresponding y-coordinates.

Examples Related to Latus Rectum

1: What will be the length of the latus rectum of the following parabola x² = – 4y.

From the equation given above, we can conclude that the parabola is symmetric about the Y-axis and it is open in a downward position.

x² = – 4y

x² = – 4ay

4a = 4

Thus, the length of the latus rectum of a given parabola is 4 units.

2: Find the equation of the parabola having its focus ( 0, -3) and the directrix of the parabola is on the line y = 3.

As the focus of the parabola is on the y- axis and is also below the directrix, the parabola will be opened downward, and the value of a = -3

Hence, equation of a parabola is given as x² = 12x

Length of the latus rectum of a parabola is |4 (-3)| = 12

3: Find the latus rectum of parabola y² = 20x.

Given equation of a parabola is y² = 20x

Comparing this with the standard equation of a parabola y²=4ax we have

4a = 20

a = 5

For equation of a parabola y²= 4ax the equation of latus rectum is x = -a, which is

x = -5

x + 5 = 0

Therefore the equation of latus rectum of parabola is x + 5 = 0

Practice Questions on Latus Rectum

Q1. Calculate the length of the latus rectum of the following parabola x²– 2x + 8y + 17 = 0

Q2. Find the equation of directrix of a parabola x² = – 16y

Q3. Find the length of latus rectum of the ellipse x²/49 + y²/25 = 1

Conclusion

In the conclusion, the latus rectum is a term that refers to the conic area of the spine. It is necessary to first learn what conic sections are in order to understand what a latus rectum is. latus rectum provides valuable insights into the dimensions and shape of these curves. Conic sections are two-dimensional curves that are formed when a cone meets a plane in a circular way.

Latus Rectum- FAQs

What is Latus Rectum?

Latus Rectum is a significant line segment associated with conic sections, specifically parabolas, ellipses, and hyperbolas. It is a line segment that passes through the focus of the conic section and is perpendicular to the major axis or the axis of symmetry.

What are Applications of Latus Rectum?

• Optics: Understanding the latus rectum helps in designing reflective properties of mirrors and lenses.
• Astronomy: In elliptical orbits, the latus rectum helps describe the orbit’s shape and the distance from the focus (e.g., a star or planet) at various points.

Can Latus Rectum be Used to Graph Conics?

Yes, knowing the length and position of the latus rectum helps in sketching conics accurately. For parabolas, it defines the width at a distance from the focus. For ellipses and hyperbolas, it helps in drawing the conic relative to its foci.

What is the Significance of Latus Rectum in Conic Sections?

Latus rectum is significant because:

• It provides a measurement of the conic’s curvature at the focus.
• In ellipses and hyperbolas, it helps relate the semi-major and semi-minor axes to the conic’s foci.
• In parabolas, it helps in finding the width of the parabola at a given distance from the vertex.

Is it true that all Conic Units have a Latus Rectum?

Yes, every conic unit contains a latus rectum. It is the chord parallel to the directrix that goes through the focus.

How Find Length of Latus Rectum of an Hyperbola?

Length of latus rectum of a hyperbola is defined as the square of the transverse axis’s length divided by the conjugate axis’s length.