A binary tree is a non-linear hierarchical data structure in which each node has at most two children known as the left child and the right child. As the binary tree has non-linear structure it can be traversed in multiple ways one such way is in-order traversal which is a depth first (DFS) traversal technique that follows the Left-Root-Right pattern.

In this article, we will learn how to implement in-order binary tree traversal in C++ and analyze its space and time complexity.

Inorder Traversal of Binary Tree in C++

In-order traversal is a DFS tree traversal technique for the binary tree where the left subtree is traversed first followed by the root node and the right subtree at the end.

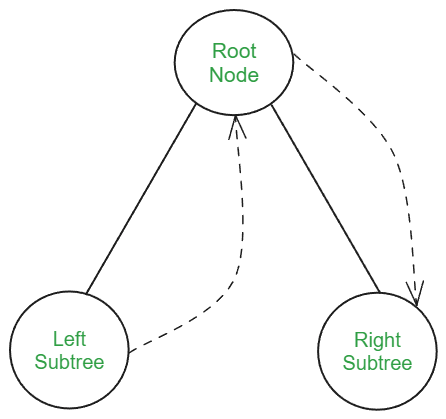Inorder Traversal

1. Traverse the left subtree.
2. Visit the root node.
3. Traverse the right subtree.

Consider the following example:

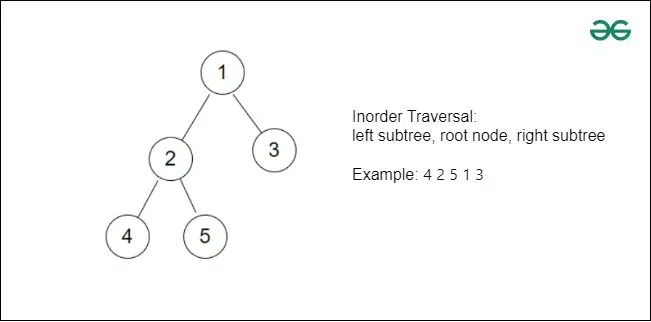Inorder Traversal Example

For inorder traversal of the above tree:

1. Start with the leftmost node, which is 4.
2. Move up to its parent, which is 2.
3. Visit the right child of 2, which is 5.
4. Move up to the root node, which is 1.
5. Finally, visit the right subtree, which is node 3.

So, the inorder traversal of the tree is: 4, 2, 5, 1, 3.

Algorithm for Inorder Binary Tree Traversal

Below is the algorithm of the inorder binary tree traversal:

inorder(TreeNode* root) {
    if (root == NULL)
        return;
    inorder(root->left);
    cout << root->val << " ";
    inorder(root->right);
}

C++ Program For Inorder Traversal of a Binary Tree

The following program illustrates how to implement the inorder traversal of a binary tree in C++.

// C++ Program for inorder traversal of a Binary Tree

#include <iostream>
using namespace std;

//  BINARY TREE IMPLEMENTATION

// Class definition for a binary tree node
class Node {
public:
    int data;
    Node* left;
    Node* right;

    // Constructor to create a new node
    Node(int data)
    {
        this->data = data;
        this->left = nullptr;
        this->right = nullptr;
    }
};

// Class definition for a binary tree
class BinaryTree {
public:
    Node* root;

    // Constructor to initialize the root
    BinaryTree() { root = nullptr; }

    // INORDER TRAVERSAL
    // Function to perform inorder traversal
    void inorderTraversal(Node* node)
    {
        if (node != nullptr) {

            inorderTraversal(node->left);
            cout << node->data << " ";
            inorderTraversal(node->right);
        }
    }
};

int main()
{
    // Initialize a binary tree
    BinaryTree btree;
    btree.root = new Node(1);
    btree.root->left = new Node(2);
    btree.root->right = new Node(3);
    btree.root->left->left = new Node(4);
    btree.root->left->right = new Node(5);

    // Perform the inorder traversal
    cout << "The inorder traversal of the binary tree is:"
         << endl;
    btree.inorderTraversal(btree.root);
    cout << endl;

    return 0;
}

The inorder traversal of the binary tree is:
4 2 5 1 3 

Time Complexity: O(N), here N denotes the total number of nodes in the binary tree because we visit each node exactly once.
Auxiliary Space: O(1), if the recursive stack space is not considered. If the stack space is considered then O(log N), for a balanced tree and O(N) for a skewed tree.

Refer to this article for more detailed time and space complexity analysis.

Applications of Inorder Traversal

Following are some of the common applications of inorder traversal:

• Copying and Cloning: In-order traversal can be used to create a copy of the binary tree or to clone it by visiting each node in the correct order.
• Sorted Elements: The inorder traversal of a binary search tree always returns the elements in non-decreasing sorted order.
• Expression Trees: Inorder traversal is used to retrieve the infix expression from an expression tree, which is important in expression evaluation and compiler design.
• Counting Nodes in a Range: It can be used to count the number of nodes within a certain range in a BST by skipping unnecessary subtrees.

Related Articles:

You can go through these articles to improve your understanding about the inorder traverals:

• Types of Tree Traversals
• Iterative inorder traversal
• Construct binary tree from inorder and inorder traversal
• Morris traversal for inorder traversal of tree