|
Artificial Neural Networks (ANNs) have revolutionized the field of machine learning, offering powerful tools for pattern recognition, classification, and predictive modeling. Among the various types of neural networks, the Feedforward Neural Network (FNN) is one of the most fundamental and widely used. In this article, we will explore the structure, functioning, and applications of Feedforward Neural Networks, providing a comprehensive understanding of this essential machine learning model.
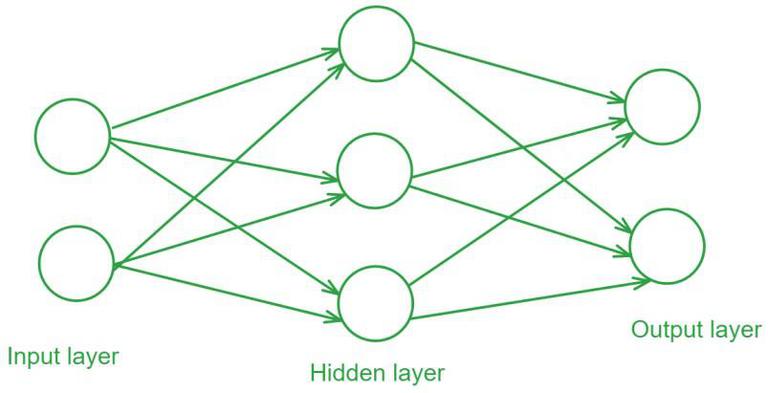
What is a Feedforward Neural Network?A Feedforward Neural Network (FNN) is a type of artificial neural network where connections between the nodes do not form cycles. This characteristic differentiates it from recurrent neural networks (RNNs). The network consists of an input layer, one or more hidden layers, and an output layer. Information flows in one direction—from input to output—hence the name “feedforward.”
Structure of a Feedforward Neural Network- Input Layer: The input layer consists of neurons that receive the input data. Each neuron in the input layer represents a feature of the input data.
- Hidden Layers: One or more hidden layers are placed between the input and output layers. These layers are responsible for learning the complex patterns in the data. Each neuron in a hidden layer applies a weighted sum of inputs followed by a non-linear activation function.
- Output Layer: The output layer provides the final output of the network. The number of neurons in this layer corresponds to the number of classes in a classification problem or the number of outputs in a regression problem.
Each connection between neurons in these layers has an associated weight that is adjusted during the training process to minimize the error in predictions.
 Feed Forward Neural Network Activation FunctionsActivation functions introduce non-linearity into the network, enabling it to learn and model complex data patterns. Common activation functions include:
- Sigmoid: σ(x)=[Tex]\sigma(x) = \frac{1}{1 + e^{-x}}[/Tex]
- Tanh: [Tex]\text{tanh}(x) = \frac{e^x – e^{-x}}{e^x + e^{-x}}
[/Tex]
- ReLU (Rectified Linear Unit): [Tex]\text{ReLU}(x) = \max(0, x)[/Tex]
- Leaky ReLU: [Tex]\text{Leaky ReLU}(x) = \max(0.01x, x)[/Tex]
Training a Feedforward Neural NetworkTraining a Feedforward Neural Network involves adjusting the weights of the neurons to minimize the error between the predicted output and the actual output. This process is typically performed using backpropagation and gradient descent.
- Forward Propagation: During forward propagation, the input data passes through the network, and the output is calculated.
- Loss Calculation: The loss (or error) is calculated using a loss function such as Mean Squared Error (MSE) for regression tasks or Cross-Entropy Loss for classification tasks.
- Backpropagation: In backpropagation, the error is propagated back through the network to update the weights. The gradient of the loss function with respect to each weight is calculated, and the weights are adjusted using gradient descent.
 Forward Propagation
Gradient Descent
Gradient Descent is an optimization algorithm used to minimize the loss function by iteratively updating the weights in the direction of the negative gradient. Common variants of gradient descent include:
- Batch Gradient Descent: Updates weights after computing the gradient over the entire dataset.
- Stochastic Gradient Descent (SGD): Updates weights for each training example individually.
- Mini-batch Gradient Descent: Updates weights after computing the gradient over a small batch of training examples.
Evaluation of Feedforward neural networkEvaluating the performance of the trained model involves several metrics:
- Accuracy: The proportion of correctly classified instances out of the total instances.
- Precision: The ratio of true positive predictions to the total predicted positives.
- Recall: The ratio of true positive predictions to the actual positives.
- F1 Score: The harmonic mean of precision and recall, providing a balance between the two.
- Confusion Matrix: A table used to describe the performance of a classification model, showing the true positives, true negatives, false positives, and false negatives.
Code Implementation of Feedforward neural networkThis code demonstrates the process of building, training, and evaluating a neural network model using TensorFlow and Keras to classify handwritten digits from the MNIST dataset. Initially, the MNIST dataset is loaded and normalized by scaling the pixel values to the range [0, 1]. The model architecture is defined using the Sequential API, consisting of a Flatten layer to convert the 2D image input into a 1D array, followed by a Dense layer with 128 neurons and ReLU activation, and a final Dense layer with 10 neurons and softmax activation to output probabilities for each digit class. The model is compiled with the Adam optimizer, SparseCategoricalCrossentropy loss function, and SparseCategoricalAccuracy metric. The model is then trained for 5 epochs on the training data. Finally, the model’s performance is evaluated on the test set, and the test accuracy is printed.
Python
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.losses import SparseCategoricalCrossentropy
from tensorflow.keras.metrics import SparseCategoricalAccuracy
# Load and prepare the MNIST dataset
mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
# Build the model
model = Sequential([
Flatten(input_shape=(28, 28)),
Dense(128, activation='relu'),
Dense(10, activation='softmax')
])
# Compile the model
model.compile(optimizer=Adam(),
loss=SparseCategoricalCrossentropy(),
metrics=[SparseCategoricalAccuracy()])
# Train the model
model.fit(x_train, y_train, epochs=5)
# Evaluate the model
test_loss, test_acc = model.evaluate(x_test, y_test)
print(f'\nTest accuracy: {test_acc}')
Output:
Test accuracy: 0.9767000079154968 ConclusionFeedforward neural networks are fundamental building blocks in the field of machine learning. Despite their simplicity, they are powerful tools for a variety of tasks, including classification and regression. By understanding their architecture, activation functions, and training process, one can appreciate the capabilities and limitations of these networks. Continuous advancements in optimization techniques and activation functions have made feedforward networks more efficient and effective, contributing to the broader field of artificial intelligence.
Feedforward neural network FAQs What is a feedforward neural network?A feedforward neural network is a type of neural network where information flows in one direction from the input to the output layers, without cycles or loops.
How does a Feedforward Neural Network work?In a Feedforward Neural Network, data is passed through a series of layers:
- Input Layer: Receives the initial data.
- Hidden Layers: Process the data received from the input layer. These layers can be one or more, each consisting of neurons that apply activation functions to their inputs.
- Output Layer: Produces the final output.
The data flows in one direction, from the input layer to the output layer, without any feedback loops.
What are activation functions?Activation functions are mathematical equations that determine the output of a neural network’s node. They introduce non-linear properties to the network, enabling it to learn complex patterns. Common activation functions include ReLU (Rectified Linear Unit), Sigmoid, and Tanh.
What is the role of the loss function?The loss function measures how well the neural network’s predictions match the actual target values. It is a crucial component in training neural networks, as it provides a quantifiable metric to guide the optimization process. Common loss functions include Mean Squared Error (MSE) for regression tasks and Cross-Entropy Loss for classification tasks.
What is backpropagation?Backpropagation is the algorithm used to train Feedforward Neural Networks. It involves calculating the gradient of the loss function with respect to each weight by the chain rule, then updating the weights to minimize the loss using an optimization algorithm like Gradient Descent or Adam.
|


