A factor tree is a simple and visual method used to find the prime factors of a number. It is a helpful tool in mathematics, especially for breaking down large numbers into their basic building blocks, known as prime factors. By repeatedly dividing a number into smaller factors until all remaining factors are prime, a factor tree helps students and learners understand the fundamental concepts of multiplication and prime numbers.

For example, to factorize 36, you would start by dividing it by 2 (the smallest prime factor), resulting in 18. Continue dividing by 2 to get 9, and then divide by 3 to get 3. The factor tree for 36 would show that its prime factors are 2, 2, 3, and 3.

In this article, we will discuss all things about factor trees, such as how to create them, their importance in prime factorization, step-by-step examples, and their applications in solving mathematical problems.

What is a Factor Tree?

A factor tree is a graphical method used to break down a composite number into its prime factors. This visual representation simplifies the process of prime factorization, making it easier to see how a number can be divided into smaller prime numbers.

It starts with the original number at the top and branches out into pairs of factors that multiply to form the number. This branching process continues until all the end branches are prime numbers, which cannot be factored further.

Definition of Factor Tree

A factor tree is a diagram where the number is factored by continuously factoring composite numbers into smaller factors until all factors are prime.

How to Create a Factor Tree?

Here are the steps way to follow to create a factor tree:

Step 1: Start with the number you want to factor.

Step 2: Identify the smallest prime number that divides evenly into the composite number. Write this factor and the quotient.

Step 3: Take the quotient from the previous step and divide it by the smallest prime number possible.

Step 4: Continue breaking down composite factors until remaining factor is prime number.

Uses of Factor Tree

Factor tree is a valuable tool in mathematics for several reasons, particularly in the context of prime factorization and understanding the properties of numbers. Here are some of its main uses:

• Prime Factorization: A factor tree helps in breaking down a composite number into its prime factors. This is fundamental in various areas of mathematics, including simplifying fractions, finding least common multiples (LCMs), and greatest common divisors (GCDs).
• Finding LCM and GCD: Factor trees are useful in determining the least common multiple and greatest common divisor of two or more numbers, aiding in solving problems involving ratios, proportions, and multiple calculations.

Examples of Factor Tree

Factor trees provide a systematic approach to break down numbers into their prime factors. Let’s look at some specific examples to understand the process better.

Factor Tree of 120

To factorize the number 120 using a factor tree:

1. Start with 120.
2. Divide by 2 (smallest prime factor): 120 ÷ 2 = 60.
3. Divide by 2 (smallest prime factor): 60 ÷ 2 = 30.
4. Divide 30 by 2: 30 ÷ 2 = 15.
5. Divide 15 by 3 (next smallest prime factor): 15 ÷ 3 = 5.
6. The numbers at the end of the branches (2, 2, 3, and 5) are all prime.

So, the prime factorization of 120 is 2 × 2 × 2 × 3 × 5.

Factor Tree of 72

To factorize the number 72 using a factor tree:

1. Start with 72.
2. Divide by 2 (smallest prime factor): 72 ÷ 2 = 36.
3. Divide 36 by 2: 36 ÷ 2 = 18.
4. Divide 18 by 2: 18 ÷ 2 = 9.
5. Divide 9 by 3 (next smallest prime factor): 9 ÷ 3 = 3.
6. Divide 3 by 3: 3 ÷ 3 = 1.

The prime factors of 72 are 2, 2, 2, 3, and 3.

So, the prime factorization of 72 is 2 × 2 × 2 × 3 × 3.

Factor Tree of 24

To factorize the number 24 using a factor tree:

1. Start with 24.
2. Divide by 2 (smallest prime factor): 24 ÷ 2 = 12.
3. Divide 12 by 2: 12 ÷ 2 = 6.
4. Divide 6 by 2: 6 ÷ 2 = 3.
5. Divide 3 by 3: 3 ÷ 3 = 1.

The prime factors of 24 are 2, 2, 2, and 3.

So, the prime factorization of 24 is 2 × 2 × 2 × 3.

Factor Tree of 18

To factorize the number 18 using a factor tree:

1. Start with 18.
2. Divide by 2 (smallest prime factor): 18 ÷ 2 = 9.
3. Divide 9 by 3 (next smallest prime factor): 9 ÷ 3 = 3.
4. Divide 3 by 3: 3 ÷ 3 = 1.

The prime factors of 18 are 2, 3, and 3.

So, the prime factorization of 18 is 2 × 3 × 3.

Applications of Factor Trees

Factor trees have several important applications in mathematics, including

• Finding Greatest Common Divisor (GCD)
• Finding Least Common Multiple (LCM)

Let’s discuss these applications in detail with example.

Finding Greatest Common Divisor (GCD) using Factor Tree

The greatest common divisor (GCD) is the largest number that divides two or more integers without leaving a remainder. To find the GCD using a factor tree:

Step 1: Factorize each number into its prime factors. [Using factor tree]

Step 2: List the prime factors common to each number.

Step 3: Multiply the common prime factors to find the GCD.

Example : Finding GCD of 48 and 180 suing factor tree

Factor Tree for 48 and 180

Step 1: Factorize each number [ Using Factor tree ]

• Factorisation of 48 = 2 × 2 × 2 × 2 × 3
• Factorisation of 180 = 2 × 2 × 3 × 3 × 5

Step 2: Identify common prime factors:

Common factors: 2² and 3

Step 3: Multiply common prime factors to find GCD,

GCD (48, 180) = 2² × 3 = 4 × 3 = 12

Finding Least Common Multiple (LCM) using Factor Tree

The least common multiple (LCM) is the smallest number that is a multiple of two or more integers. To find the LCM using a factor tree:

• Step 1: Factorize each number into its prime factors.
• Step 2: Include the highest power of each prime factor from both numbers as common factors
• Step 3: Multiply factors from step 2 and remaining factors to find the LCM.

Example: Finding LCM of 15 and 20.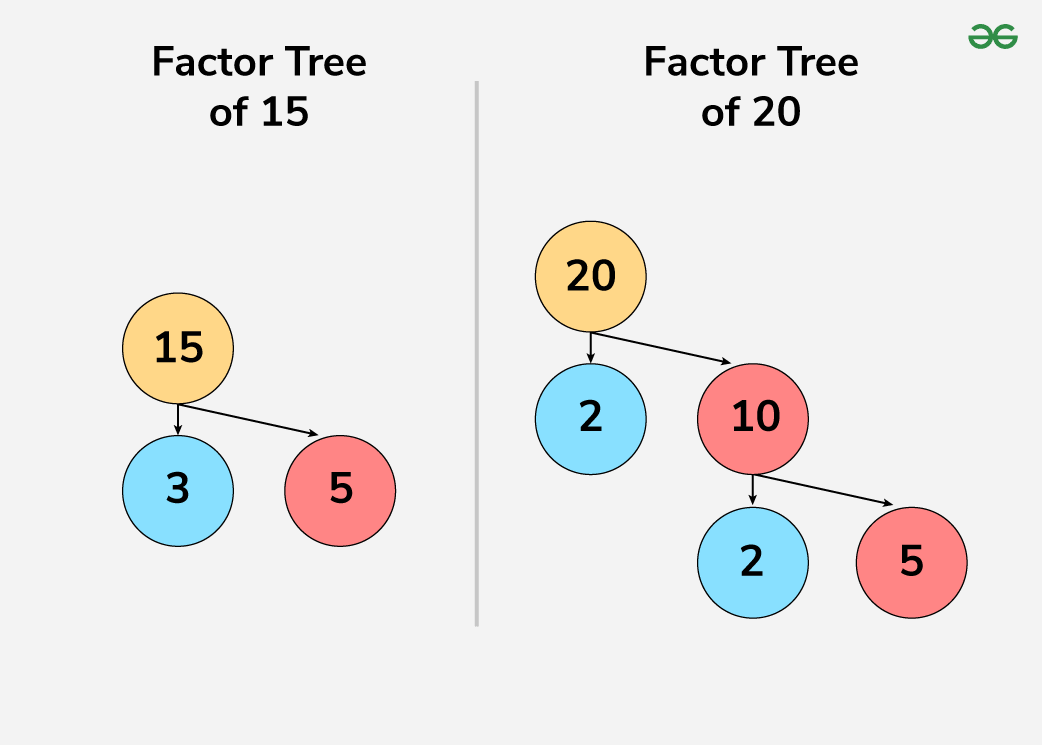

Factor Tree for 15 and 20

Step 1: Factorize each number [ Using Factor tree ]

• Factorisation of 15 = 3 × 5
• Factorisation of 20 = 2 × 2 × 5

Step 2: Identify common prime factors:

Common Prime factors are 2², 3, 5

Step 3: Multiply common prime factors with all the remaining factors, to find LCM,

LCM(15, 20) = 2² × 3 × 5 = 4 × 3 × 5 = 60

Read More,

• HCF and LCM
• HCF and LCM Questions
• Relation between LCM and HCF

Practice Problems on Factor Tree

Problems 1: Factorize 45 using a factor tree.

Problems 2: Create a factor tree for 100.

Problems 3: Determine the prime factorization of 81 using a factor tree.

Problems 4: Use a factor tree to find the prime factors of 56.

Problems 5: Construct a factor tree for 144.

Problems 6: Find the prime factors of 90 using a factor tree.

Conclusion

Factor trees are one of the many methods to find prime factorization of any number. Other methods use arithmetic operations to find the factors, whereas factor trees use visual approach. They provide a clear and visual method to break down complex numbers into their prime factors, making the learning process simpler and more intuitive. Using factor trees not only aids in educational development but also enhances problem-solving skills by providing a systematic approach to factorization.

Factor Tree – FAQs

What is the purpose of a factor tree?

A Factor tree break down a composite number into its prime factors, simplifying various mathematical calculations like finding the GCD, and LCM, and simplifying fractions.

Can 1 be in a factor tree?

No, 1 is not included in a factor tree because it is not a prime number and does not help in breaking down a composite number into prime factors.

Do factor trees show all factors?

No, factor trees only show the prime factors of a number, not all factors.

Is factor and square root the same?

No, the factors are the numbers that when multiplied together result in a product, while the square root is a value that when squared gives the original number.

Can you factor in a radical?

Yes, radicals can be factored by simplifying the expression inside the radical sign, often using prime factorization for the numbers involved.