Given a binary tree, find the sum of the product of each node and its mirror image (The mirror of a node is a node which exists at the mirror position of the node in opposite subtree at the root), not taking into account a pair more than once. The root node is the mirror image of itself. The answer may be very large, compute the answer modulo 10 ⁹ + 7.

Examples:

Input:

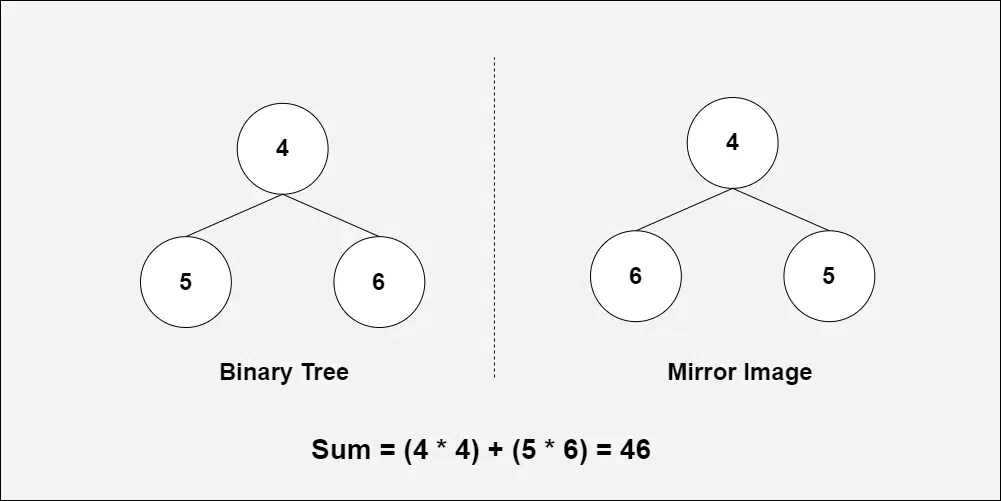Output: 46
Explanation: Sum = (4*4) + (5*6) = 46

Input:

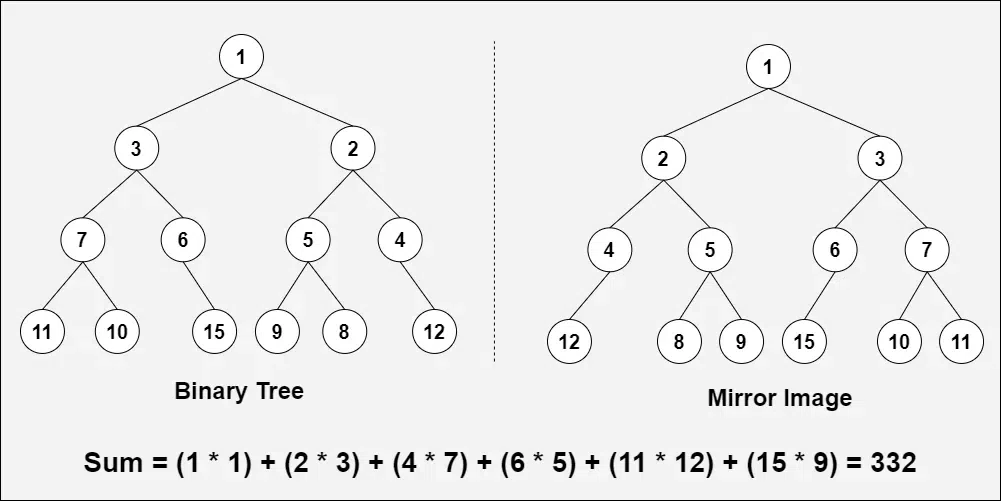Output: 332
Explanation: Sum = (1*1) + (3*2) + (7*4) + (6*5) + (11*12) + (15*9) = 332

Approach:

The mirror of a node in a binary tree is the node located at the same position but in the opposite subtree when considering the root as the center of mirroring. For a given node, its mirror can be identified by traversing the tree symmetrically.

We need to calculate the sum of the product of each node with its mirror image. The root node is its own mirror, so its contribution to the sum is square of root’s value . For other nodes, their product with their mirror should be included only once.

Use a recursive function to simultaneously traverse the left and right subtrees. For each pair of nodes (one from the left subtree and one from the right subtree), compute the product and add it to the sum. Ensure that each pair is only counted once.

Step-by-step algorithm:

• Create a helper function that takes two nodes as parameters and computes the sum of products of these nodes and their children. This function will be called initially with the left and right children of the root. We recursively call this function on left child of left tree and right child of right tree & also on right child of left tree and left child of right tree.
• If either of the nodes in the pair is null, return 0 as the product involving a null node is 0.
• Calculate the product of the current pair of nodes and add it to the recursive results of their children.
• In the main function, initialize the sum with the square of the root value. Use the helper function to add the sum of products for the left and right subtrees.
• Given that the result can be very large, compute the answer modulo 10 ⁹ +7 and return it.

Following is the implementation of above approach:

#include <iostream>

using namespace std;

// Define the structure for Node
struct Node {
    long long data;
    Node *left, *right;

    // Constructor to initialize data and left/right
    // pointers
    Node(long long val) : data(val), left(nullptr), right(nullptr) {}
};

void solve(Node* leftTree, Node* rightTree,
           long long int& sum)
{
    if (!leftTree || !rightTree)
        return;
    sum = sum + (leftTree->data * rightTree->data);
    solve(leftTree->left, rightTree->right, sum);
    solve(leftTree->right, rightTree->left, sum);
}

int mod = 1e9 + 7;

// Function to perform image multiplication
long long imgMultiply(Node* root)
{
    // Base case
    if (!root)
        return 0;

    // Initialize sum with square of root node's data
    long long int sum = root->data * root->data;

    // Recursively calculate sum of products of
    // corresponding nodes
    solve(root->left, root->right, sum);

    // Return the result modulo mod
    return sum % mod;
}

int main()
{
    // Example usage
    // Create a sample binary tree
    Node* root = new Node(1);
    root->left = new Node(2);
    root->right = new Node(3);
    root->left->left = new Node(4);
    root->left->right = new Node(5);
    root->right->left = new Node(6);
    root->right->right = new Node(7);

    /*
    The binary tree created looks like this:
                    1
                   / \
                  2   3
                 / \ / \
                4  5 6  7
    */

    // Call the imgMultiply function and print the result
    cout << "Result: " << imgMultiply(root) << endl;

    // Clean up allocated memory
    delete root->right->right;
    delete root->right->left;
    delete root->left->right;
    delete root->left->left;
    delete root->right;
    delete root->left;
    delete root;

    return 0;
}

import java.util.Objects;

// Define the structure for Node
class Node {
    long data;
    Node left, right;

    // Constructor to initialize data and left/right
    // pointers
    Node(long val)
    {
        data = val;
        left = null;
        right = null;
    }
}

public class Main {
    static int mod = 1000000007;

    // Recursive function to calculate the sum of products
    // of corresponding nodes
    static void solve(Node leftTree, Node rightTree,
                      long[] sum)
    {
        if (Objects.isNull(leftTree)
            || Objects.isNull(rightTree))
            return;
        sum[0] = (sum[0] + (leftTree.data * rightTree.data))
                 % mod;
        solve(leftTree.left, rightTree.right, sum);
        solve(leftTree.right, rightTree.left, sum);
    }

    // Function to perform image multiplication
    static long imgMultiply(Node root)
    {
        // Base case
        if (Objects.isNull(root))
            return 0;

        // Initialize sum with square of root node's data
        long[] sum = { root.data * root.data };

        // Recursively calculate sum of products of
        // corresponding nodes
        solve(root.left, root.right, sum);

        // Return the result modulo mod
        return sum[0];
    }
    public static void main(String[] args)
    {
        // Example usage
        // Create a sample binary tree
        Node root = new Node(1);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.left = new Node(4);
        root.left.right = new Node(5);
        root.right.left = new Node(6);
        root.right.right = new Node(7);

        /*
        The binary tree created looks like this:

                        1
                       / \
                      2   3
                     / \ / \
                    4  5 6  7
        */

        // Call the imgMultiply function and print the
        // result
        System.out.println("Result: " + imgMultiply(root));
    }
}

# Define the structure for Node
class Node:
    def __init__(self, val: int) -> None:
        self.data: int = val
        self.left: Optional[Node] = None
        self.right: Optional[Node] = None


mod = 10**9 + 7

# Recursive function to calculate the sum of products of corresponding nodes
def solve(leftTree, rightTree, sum) -> None:
    if not leftTree or not rightTree:
        return
    sum[0] = sum[0] + (leftTree.data * rightTree.data)
    solve(leftTree.left, rightTree.right, sum)
    solve(leftTree.right, rightTree.left, sum)

# Function to perform image multiplication
def imgMultiply(root) -> int:
    # Base case
    if not root:
        return 0

    # Initialize sum with square of root node's data
    sum = [root.data * root.data]

    # Recursively calculate sum of products of corresponding nodes
    solve(root.left, root.right, sum)

    # Return the result modulo mod
    return sum[0] % mod


# Example usage
# Create a sample binary tree
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)


# Call the imgMultiply function and print the result
print("Result:", imgMultiply(root))

# Clean up allocated memory
del root.right.right
del root.right.left
del root.left.right
del root.left.left
del root.right
del root.left
del root

Result: 65

Time Complexity: O(n), as we are traversing the whole tree to calculate product of the mirror image of the nodes.
Auxiliary Space: O(h), as we are using recursion stack space.