|
|
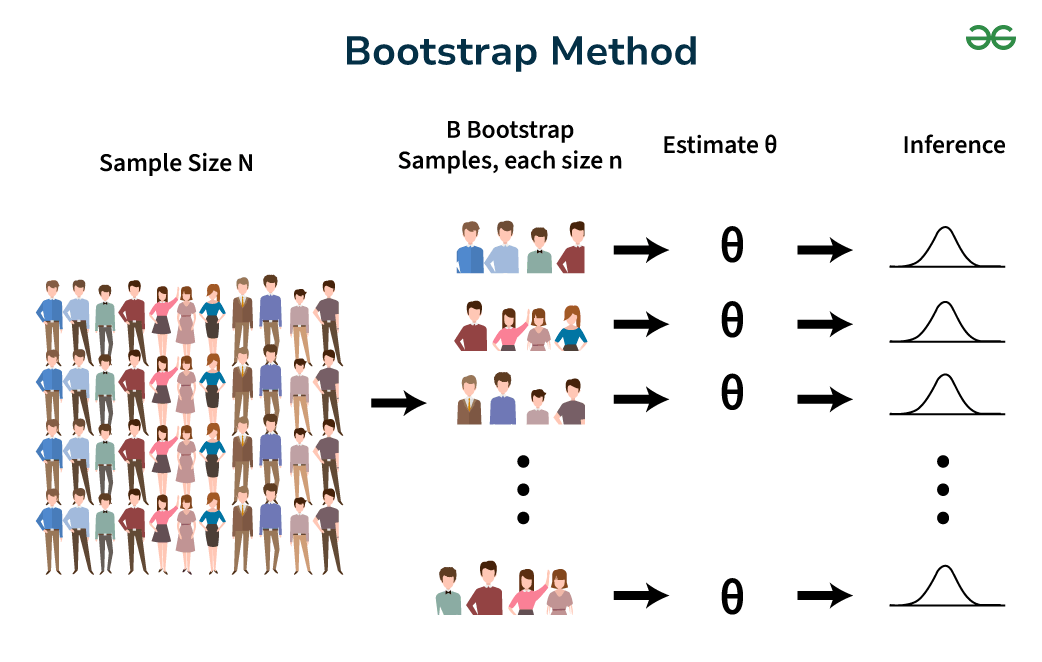
Bootstrap Method is a powerful statistical technique widely used in mathematics for estimating the distribution of a statistic by resampling with replacement from the original data. The bootstrap method is a resampling technique that allows you to estimate the properties of an estimator (such as its variance or bias) by repeatedly drawing samples from the original data. It was introduced by Bradley Efron in 1979 and has since become a widely used tool in statistical inference. The bootstrap method is useful in situations where the theoretical sampling distribution of a statistic is unknown or difficult to derive analytically. Table of Content What is Bootstrap Method or Bootstrapping?Bootstrap Method or Bootstrapping is a statistical procedure that resamples a single data set to create many simulated samples. This process allows for the calculation of standard errors, confidence intervals, and hypothesis testing,” according to a post on bootstrapping statistics from statistician Jim Frost. Bootstrapping is a resampling technique used to estimate population statistics by sampling from a dataset with replacement. It can be used to estimate summary statistics such as the mean and standard deviation. It is used in applied machine learning to estimate the quality of a machine learning model at predicting data that is not included in the training data.
The bootstrap approach is a very useful alternative to traditional hypothesis testing methods, as it is relatively simple and avoids some of the pitfalls of traditional approaches. Statistical inference generally relies on the sampling distribution and standard error of the characteristic of interest. In the traditional or large sample approach, a sample of size n is taken from the population, this sample is used to calculate an estimate of the population, and conclusions are drawn based on it. In reality, only the sample was observed. How Bootstrapping Statistics Works?In the bootstrap method, a sample of size n is drawn from a population. We’ll call this sample S. Then, rather than using theory to determine all possible estimates, a sampling distribution is created by resampling observations from S with replacement m times, where each resampled set contains n observations. With proper sampling, S will be representative of the population. Thus, by resampling S m times with replacement, it is as if m samples were drawn from the original population, and the derived estimates will represent the theoretical distribution from the traditional approach. Increasing the number of replicate samples m does not increase the information content of the data; that is, resampling the original dataset 100,000 times is not as useful as resampling it 1,000 times. The information content of a dataset depends on the sample size n, which remains constant for each replicate sample. Thus, the benefit of a larger number of replicate samples is that they provide a more accurate estimate of the sampling distribution. Bootstrap MethodBootstrap Method or Bootstrapping is a statistical technique for estimating an entire population quantity by averaging estimates from multiple smaller data samples. Importantly, the sample is created by extracting observations one at a time from a larger data sample and adding them back to the selected data sample. This allows a given observation to be included multiple times in a given smaller sample. This sampling technique is called sampling with replacement.  Bootstrap Method The process of creating a sample can be summarized as follows: Choose a sample size. If the sample size is smaller than the size you selected Randomly select observations from the dataset Add them to the sample Bootstrapping methods can be used to estimate population abundance. This is done by repeatedly taking small samples, computing statistics, and averaging the computed statistics. The procedure can be summarized as follows:
Bootstrap method is additionally a suitable for controlling and actually look at the solidness of the outcomes. In spite of the fact that for most issues it is difficult to know the genuine certainty span, bootstrap is asymptotically more exact than the standard stretches got utilizing test change and presumptions of ordinariness. Differences between Bootstrap method and Traditional Hypothesis TestingVarious differences between Bootstrapping and Traditional Hypothesis Testing are added in the table below:
Example of samples created using Bootstrap methodExample of how bootstrap samples are created and used to estimate a statistic of interest. Solution:
In this example, we used bootstrapping to estimate the median by resampling from the original data multiple times and calculating the statistic of interest (median) for each bootstrap sample. By repeating this process many times, we can build an empirical sampling distribution of the median, which can be used to construct confidence intervals or perform hypothesis tests without relying on assumptions about the underlying population distribution. Example of Using Bootstrapping to Create Confidence IntervalsSolution:
Confidence IntervalA confidence interval is a range of values used to estimate an unknown population parameter, such as the mean, proportion, or regression coefficient. The confidence interval is calculated from a given set of sample data and is constructed in a way that it has a specified probability of containing the true population parameter. The level of confidence (usually expressed as a percentage) is the complement of the significance level, which represents the probability that the confidence interval does not contain the true population parameter. For example, a 95% confidence interval implies that if the process of computing the confidence interval is repeated multiple times on different samples from the same population, 95% of the computed intervals will contain the true population parameter. The width of the confidence interval provides an estimate of the precision or uncertainty associated with the sample estimate. A narrower confidence interval indicates higher precision, while a wider interval suggests greater uncertainty. The reason for this is that we split 100% – 90% = 10% in half so that we will have the middle 90% of all of the bootstrap sample means. Advantages of Bootstrap MethodBootstrap method offers several key advantages that make it a valuable tool in statistical analysis and mathematical research:
Limitations of Bootstrap MethodsVarious limitations of Bootstrap Methods are:
Applications of Bootstrapping MethodVarious application of Bootstrapping Method includes: In Hypothesis TestingOne of the best methods for hypothesis testing is the bootstrap method. Unlike the traditional methods, the bootstrap method allows one to evaluate the accuracy of a dataset using the replacement technique. In Standard ErrorThe bootstrap method is used to efficiently determine the standard error of a dataset as it involves the replacement technique. The Standard Error (SE) of a statistical data set represents the estimated standard deviation. In Machine LearningUnlike statistics, Bootstrapping in Machine Learning works quite differently. In the case of Machine Learning, the bootstrapping method accommodates the bootstrapped data for training Machine Learning Models and then tests the model using the leftover data points. In Bootstrapping AggregationBagging in data mining, or Bootstrapping Aggregation, is an ensemble Machine Learning technique that accommodates the bootstrap method and the aggregation technique. Bootstrap Method – FAQsWhat is Bootstrap Method?
How to Implement Bootstrap Method?
What is the Advantage of Bootstrap Method?
What is the Bootstrap Method Used for?
|
Reffered: https://www.geeksforgeeks.org
| Mathematics |
Type: | Geek |
Category: | Coding |
Sub Category: | Tutorial |
Uploaded by: | Admin |
Views: | 15 |