|
Kruskal’s Algorithm is used to find Minimum Spanning Tree in the graph. A minimum spanning tree (MST) is a spanning tree with a weight less than or equal to the weight of every other spanning tree.
Examples:
Input: N = 6, edges[][] = {{1, 2, 1}, {2, 3, 4}, {1, 4, 3}, {4, 5, 6}, {2, 5, 2}, {3, 5, 5}, {5, 6, 6}}
Output: MST with edges: {{1, 2, 1}, {2, 3, 4}, {1, 4, 3}, {2, 5, 2}, {5, 6, 6}}
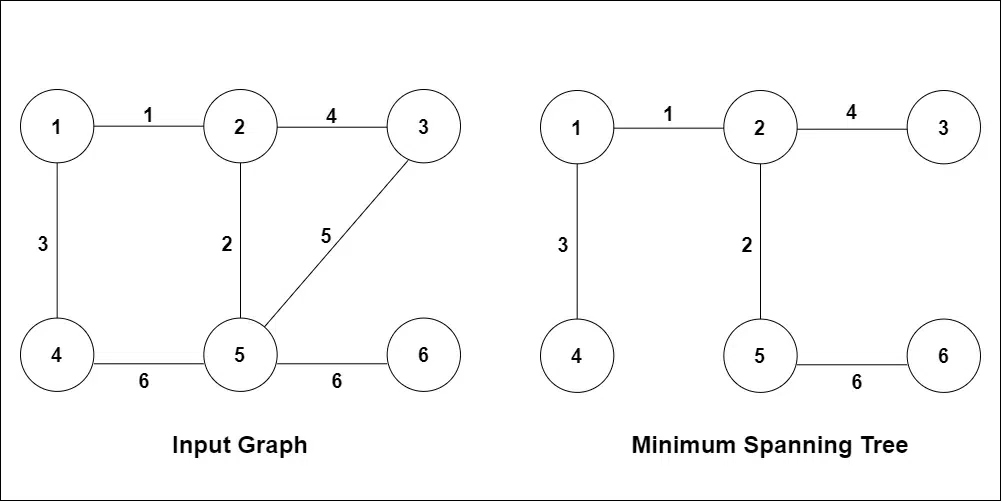
Kruskal’s Algorithm is a greedy algorithm used to find MST in the graph. Kruskal’s Algorithm sorts all edges of the given graph in increasing order. Then it keeps on adding new edges and nodes in the MST if the newly added edge does not form a cycle. It picks the minimum weighted edge at first and the maximum weighted edge at last and therefore it is a greedy algorithm. The Greedy Choice is to pick the smallest weight edge that does not cause a cycle in the MST constructed so far.
Union-Find Algorithm is used to check whether adding a new edge forms a cycle or not.
Step-by-step algorithm: - Sort all the edges in non-decreasing order of their weight.
- Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far.
- If the cycle is not formed, include this edge. Else, discard it.
- Repeat steps 2 and 3 until there are (V-1) edges in the spanning tree.
Implementation of Kruskal’s Algorithm in Python: Below is the implementation of Kruskal’s Algorithm in Python:
Python
# Python program for Kruskal's algorithm to find
# Minimum Spanning Tree of a given connected,
# undirected and weighted graph
# Class to represent a graph
class Graph:
def __init__(self, vertices):
self.V = vertices
self.graph = []
# Function to add an edge to graph
def addEdge(self, u, v, w):
self.graph.append([u, v, w])
# A utility function to find set of an element i
# (truly uses path compression technique)
def find(self, parent, i):
if parent[i] != i:
# Reassignment of node's parent
# to root node as
# path compression requires
parent[i] = self.find(parent, parent[i])
return parent[i]
# A function that does union of two sets of x and y
# (uses union by rank)
def union(self, parent, rank, x, y):
# Attach smaller rank tree under root of
# high rank tree (Union by Rank)
if rank[x] < rank[y]:
parent[x] = y
elif rank[x] > rank[y]:
parent[y] = x
# If ranks are same, then make one as root
# and increment its rank by one
else:
parent[y] = x
rank[x] += 1
# The main function to construct MST
# using Kruskal's algorithm
def KruskalMST(self):
# This will store the resultant MST
result = []
# An index variable, used for sorted edges
i = 0
# An index variable, used for result[]
e = 0
# Sort all the edges in
# non-decreasing order of their
# weight
self.graph = sorted(self.graph,
key=lambda item: item[2])
parent = []
rank = []
# Create V subsets with single elements
for node in range(self.V):
parent.append(node)
rank.append(0)
# Number of edges to be taken is less than to V-1
while e < self.V - 1:
# Pick the smallest edge and increment
# the index for next iteration
u, v, w = self.graph[i]
i = i + 1
x = self.find(parent, u)
y = self.find(parent, v)
# If including this edge doesn't
# cause cycle, then include it in result
# and increment the index of result
# for next edge
if x != y:
e = e + 1
result.append([u, v, w])
self.union(parent, rank, x, y)
# Else discard the edge
minimumCost = 0
print("Edges in the constructed MST")
for u, v, weight in result:
minimumCost += weight
print("%d -- %d == %d" % (u, v, weight))
print("Minimum Spanning Tree", minimumCost)
# Driver code
if __name__ == '__main__':
g = Graph(4)
g.addEdge(0, 1, 10)
g.addEdge(0, 2, 6)
g.addEdge(0, 3, 5)
g.addEdge(1, 3, 15)
g.addEdge(2, 3, 4)
# Function call
g.KruskalMST()
OutputEdges in the constructed MST
2 -- 3 == 4
0 -- 3 == 5
0 -- 1 == 10
Minimum Spanning Tree 19
Time Complexity: O(E * logE) or O(E * logV)
Auxiliary Space: O(V + E), where V is the number of vertices and E is the number of edges in the graph.
|
