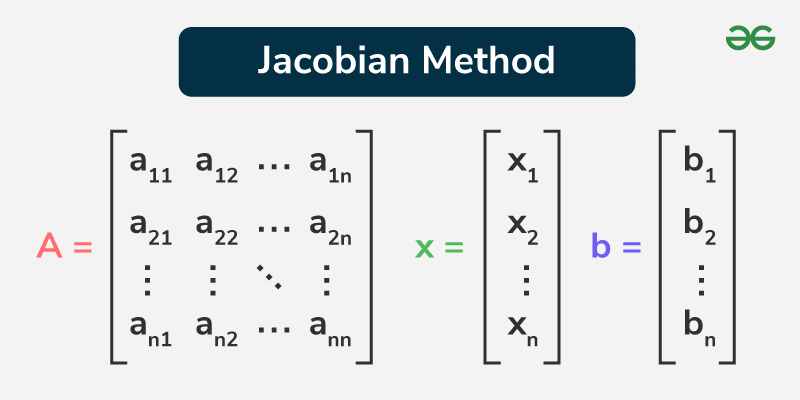
The Jacobian Method, also known as the Jacobi Iterative Method, is a fundamental algorithm used to solve systems of linear equations. This method, named after the mathematician Carl Gustav Jacob Jacobi, is particularly useful when dealing with large systems where direct methods are computationally expensive.

The Jacobian Method works by breaking down a complex set of equations into simpler parts, making it easier to approximate the solutions. The Jacobian method leverages the properties of matrices to find solutions efficiently. Here’s a simple way to understand it:

Imagine you have a set of equations, and you need to find the values of certain variables that make all these equations true simultaneously. Instead of solving everything at once, the Jacobian Method starts with an initial guess for these values. It then repeatedly refines this guess, step by step, getting closer to the actual solution with each iteration.

This article will discuss the principles, applications, and advantages of the Jacobian method, highlighting its significance in computational mathematics and engineering disciplines.

What is the Jacobian Method?

Jacobian Method, often referred to as the Jacobi Method, is an iterative algorithm used for solving systems of linear equations. It is particularly useful for large systems where direct methods (like Gaussian elimination) are computationally expensive. The method is named after Carl Gustav Jacob Jacobi, a German mathematician.

Jacobian Method

Basics of Jacobian Method

The method is used to solve a system of linear equations of the form:

Ax = b

Where A is a square matrix, x is the vector of unknowns, and b is the right-hand side vector.

The Jacobi Method decomposes the matrix A into its diagonal component D and the remainder R, such that:

A = D + R

The system of equations can then be rewritten as:

Dx = b − Rx

The iterative formula for the Jacobi Method is:

x^k+1 = D⁻¹(b − Rx^k)

Where x^k is the approximation of the solution at the k^th iteration.

Jacobi Iterative Implementation of Jacobian Method

The Jacobi iterative method is a specific implementation of the Jacobian method. It assumes that the system of linear equations can be written in the form Ax = b, where A is the coefficient matrix, x is the vector of unknown variables, and b is the vector of constants. The Jacobi method proceeds as follows:

• Assumption 1: The system of linear equations has a unique solution.
• Assumption 2: The coefficient matrix A has no zeros on its main diagonal.

Steps for Jacobi Iterative Method

We can use the following steps:

1. Rewrite the system of linear equations in the form: [Tex]x_i = (b_i – ∑_j≠i a_ij x_j) / a_ii[/Tex]
2. Make an initial guess of the solution, x⁽⁰⁾ = (x₁⁽⁰⁾, x₂⁽⁰⁾, …, x_n⁽⁰⁾).
3. Compute the first approximation, x⁽¹⁾, by substituting the initial guess into the rewritten equations.
4. Repeat step 3, using the previous approximation to compute the next approximation, until the desired accuracy is achieved.

Let’s consider an example for better understanding:

Example : Consider the system of linear equations:

• 2x + y + z = 6
• x + 3y – z = 0
• -x + y + 2z = 3

Rewriting the system in the Jacobi form, we get:

x = (6 – y – z) / 2

y = (0 – x + z) / 3

z = (3 + x – y) / 2

Starting with the initial guess x⁽⁰⁾ = (0, 0, 0), the first approximation is:

x⁽¹⁾ = (6 – 0 – 0) / 2 = 3

y⁽¹⁾ = (0 – 0 + 0) / 3 = 0

z⁽¹⁾ = (3 + 0 – 0) / 2 = 1.5

Continuing the iterations, we obtain the following approximations:

x⁽²⁾ = 1.5, y⁽²⁾ = 0.5, z⁽²⁾ = 1.0

x⁽³⁾ = 1.75, y⁽³⁾ = 0.25, z⁽³⁾ = 1.25

The iterations continue until the desired accuracy is achieved.

Jacobian Method in Matrix Form

Let the system of linear equations be Ax = b, where A is the coefficient matrix , x is the vector of unknown variables, and b is the vector of constants.

[Tex]\begin{array}{cccccc} a_{11} x_1^{(k+1)} & + & a_{12} x_2^{(k)} & + \cdots + & a_{1n} x_n^{(k)} & = b_1 \\ a_{21} x_1^{(k)} & + & a_{22} x_2^{(k+1)} & + \cdots + & a_{2n} x_n^{(k)} & = b_2 \\ \vdots & & \vdots & & \vdots & \vdots \\ a_{n1} x_1^{(k)} & + & a_{n2} x_2^{(k)} & + \cdots + & a_{nn} x_n^{(k+1)} & = b_n \end{array}[/Tex]

We can decompose the matrix A into three parts:

A = D + L + U

Where D is the diagonal matrix, L is the lower triangular matrix, and U is the upper triangular matrix.

[Tex]\begin{bmatrix} a_{11} & 0 & \cdots & 0 \\ 0 & a_{22} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & a_{nn} \end{bmatrix} \begin{bmatrix} x_1^{(k+1)} \\ x_2^{(k+1)} \\ \vdots \\ x_n^{(k+1)} \end{bmatrix} + \begin{bmatrix} 0 & a_{12} & \cdots & a_{1n} \\ a_{21} & 0 & \cdots & \vdots \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & \cdots & a_{n,n-1} & 0 \end{bmatrix} \begin{bmatrix} x_1^{(k)} \\ x_2^{(k)} \\ \vdots \\ x_n^{(k)} \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{bmatrix}[/Tex]

The Jacobi iteration can then be written as:

x^(k+1) = D^(-1) (b – (L + U)x^(k))

Where x^(k) and x^(k+1) are the kth and (k+1)^th approximations of the solution, respectively.

The element-based formula for the Jacobi method can be written as:

x_i^(k+1) = [Tex](b_i – ∑_j≠i a_ij x_j^(k)) / a_ii[/Tex]

This formula shows how the (k+1)^th approximation of the i^th variable is computed using the k^th approximations of the other variables.

Difference between Jacobian method and Gauss-Seidel Method