Number that multiplies each term in the expansion of a binomial expression raised to a power is known as the coefficient in binomial expansion. The number of possibilities to pick “k” items from n elements is shown by the coefficients of the binomial theorem, which gives a formula for expanding statements such as (a + b)ⁿ) utilizing the formula (ⁿ_k) = n! / {k! (n – k)! }, these coefficients are computed. For instance, the binomial coefficients in (x + y)³ are 1, 3, 3, and 1.

In this article, we have covered the definition of the Binomial Coefficient, examples, and others in detail.

Coefficient in Binomial Expansion

Binomial theorem relies on binomial expansion coefficients ( ^????_k), representing the number of ways to choose K elements from a collection of N elements. These coefficients play a crucial role in algebra and combinatorics by expanding binomials, expressions with two terms. They determine the weighting of each term in the extended expression when raised to a whole number power.

They come in various forms, including:

• Binomial Coefficients: The traditional way to see (????k) as a combination, is determined by applying the following formula ( ^????_k)= n! / k! × (n-k)!×n!

• ​Pascal’s Triangle: It visually displays binomial coefficients, aiding in quick calculations and showing symmetry and patterns.

• Multinomial Coefficients: It extends binomial coefficients to expand polynomials with multiple terms into multinomial expressions.

Every term in the binomial expansion has a coefficient known as a binomial coefficient. The coefficient for a term like a^{n-k .} b^k in (a + b)ⁿ is represented by (^c _k) which can be calculated using the Binomial Theorem Formula specified above.

Understanding Coefficient in Binomial Expansion

1. Notation: representation of binomial coefficients as ⁿC_k where ‘n’ represents power and ‘ k ‘ means a term in expansion.

2. Meaning: The binomial theorem states that when expanding a binomial where the first term has an exponent of (n-k) and the second term has an exponent of k, the coefficient (ⁿC_k) represents the multiplier.

3. Calculation: The formula ⁿC_k = n! / [k! × (n – k)! ] calculates binomial coefficients. Factorial, denoted by “!,” multiplies a number by all positive integers smaller than itself.

Binomial Theorem

Binomial theorem, dating back to Euclid in the fourth century BC, allows for the expansion of algebraic statements like (x + y)ⁿ. This expansion breaks down the terms involving x and y exponents into a sum with coefficients for each phrase in the expansion.

Binomial theorem explains the algebraic expansion of a binomial’s powers. It states that (x + y)ⁿ can be expanded into a sum of terms in the form ax^b × y^c, with specific coefficients and exponents.

For example,

(x + y)⁴ = x⁴+ 4x³y + 6x²y² + 4xy³ + y⁴

The coefficients depend on n and the exponents are nonnegative integers that add up to n.

Binomial Theorem Formula

If a and b are real numbers and n is a positive integer, then

(a + b)ⁿ = ⁿC₀ aⁿ + ⁿC₁ a^{n – 1} b₁+ ⁿC₂ a^{n – 2} b² + . . . + ⁿC_r a^{n – r} b^r + … + ⁿC_n bⁿ

where,

ⁿC_r = n! / r! (n-r)! for 0 ≤ r ≤ n

Important Observations

Some important observations regarding coefficient of bionomila expansion are:

• Binomial expansion consists of n+1 terms, with the power of a decreasing by one in each term and the power of b increasing by one.
• Sum of the indices of a and b in each term is equal to n.
• Coefficients in the expansion follow Pascal’s triangle pattern.
• First term has a power of a equal to n and a power of b equal to 0, while the last term has a power of a equal to 0 and a power of b equal to n.

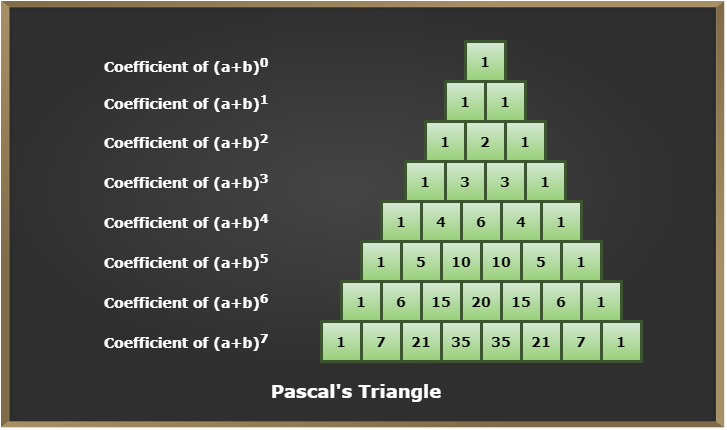
Pascal’s Triangle and Binomial Coefficients

Binomial coefficients are shown in Pascal’s Triangle. In (a + b)ⁿ expansion, rows corrrespond to coefficients. Geometry of coefficients.

Each coefficient of any row is obtained by adding two coefficients in the preceding row, one on the immediate left and the other on the immediate right and each row is bounded by 1 on both sides.

The (r + 1)^th term or general term is given by

T_{r + 1} = ⁿC_r a^{n – r} b^r

Binomial Coefficient

Binomial expression is given as:

(a + b)ⁿ = ⁿC₀aⁿ + ⁿC₁a^{n – 1}b₁+ ⁿC₂a^{n – 2} b2 + . . . + ⁿC_r a^{n – r} b^r+ … + ⁿC_n bⁿ …(i)

Coefficients ⁿC₀,ⁿC₁,ⁿC₂, … ,ⁿC_n are known as binomial or combinatorial coefficients.

Putting a = b = 1 in (i), we get

• ⁿC₀ + ⁿC₂ + ⁿC₄+ … = ⁿC₁ + ⁿC₃ + ⁿC₅ + …

Thus, the sum of all the odd binomial coefficients is equal to the sum of all the even binomial coefficients and each is equal to

2ⁿ / 2 = 2^n-1

Calculating Binomial Coefficients

Using Factorial Notation. The binomial coefficient ( ⁿ_r ) can be calculated using factorials:

( ⁿ_r )= n! / r! ( n – r)!

• where n! (n factorial) is the product of all positive integers up to n.

For example:

( ⁵₂) = 5! / (2×1) (3×2×1)

= (5×4×3×2×1) / (2×1×3) (2× 1)

= (5× 4)/ (2×1) = 10

Properties of Binomial Coefficients

Various properties of Bionomial Coefficients are:

Symmetry Property

Coefficients of the binomials show symmetry.

• ( ⁿ_k ) = ( ⁿ_n-k ) or (n/k) = (n/(n−k))

It can be seen from this feature that selecting k items from n elements is equivalent to selecting n−k elements to omit.

2. Sum of Coefficients

It says that the sum of Coefficients in the expression (a+b)ⁿ is:

• ⅀ⁿ_k=0 ( ⁿ_k ) = 2ⁿ

3. Middle Term Property

Value of n determines the middle term in a binomial expansion.

• For even n, the term at (n/2 – 1) position is the middle term.
• For odd n, the terms at [(n-1)/2] and [(n-1)/2 + 1] positions are the two middle terms.

Combinations

Binomial formula uses combinations to determine binomial coefficients in expansions. Combinations represent ways to select r variables from n variables. The equation nCr = n! / [r! (n – r)!] is used to find combinations.

• ⁿC_n = ⁿC₀ = 1
• ⁿC₁ = ⁿC_n-1 = n
• ⁿC_r = ⁿC_r-1

The basic numerical values x = 1 and y = 1 can be inserted into the binomial expansion formula (x + y)ⁿ to understand its features.

• C₁ + C₂ + C₃ + C₄ + …….C_n = 2ⁿ

• C₀ + C₂ + C₄ + …. = C₁ + C₃ + C₅ + ……. = 2_n-1

• C₀ – C₁ + C₂ – C₃ + C₄ – C₅ + …. = 0

• C₁ + 2C₂ + 3C₃ + 4C₄ + …….nC_n = n2_n-1

• C₁ – 2C₂ + 3C₃ – 4C₄ + …….(-1)^{n n}C_n = 0

• C₁² + C₂² + C₃² + C₄² + …….C_n² = (2n)! / (n!)²

Conclusion

Binomial expansion coefficients play a crucial role in mathematical reasoning and problem-solving. Understanding and mastering their concepts can lead to new insights and improved skills.

Article Related to Coefficient in Binomial Expansion:

• Binomial Theorem
• Binomial Random Variables
• Fundamental Theorem of Counting

Examples on Coefficient in Binomial Expansion

Example 1. Determine whether the expansion of (x² – 2/x)¹⁸ will contain a term containing x¹⁰?

Solution:

Let T_{r + 1} contain x¹⁰

T_{r + 1} = ¹⁸ C_r (x²)^18-r – (2/x)^r

=¹⁸C_r x^{36 – 2r} (-1)^r. 2^r x^{– r}

= (-1)^r 2^{r 18} C_rx^{36 – 3r}

Thus,

36 – 3r = 10, i.e., r =26/3

Since r is a fraction, the given expansion cannot have a term containing x¹⁰

Example 2. Find the coefficient of x² in {x + (1/x)}⁸

Solution:

Expanding {x + (1/x)}⁸ using binomila expansion formula,

⁸C₀ x⁸(1/x)⁰ + ⁸C₁ x⁷(1/x)¹ + ⁸C₂ x⁶(1/x)² + ⁸C₃ x⁵(1/x)³ + ⁸C₄ x⁴(1/x)⁴ + ⁸C₅ x³(1/x)⁵ + ⁸C₆ x²(1/x)⁶ + ⁸C₇ x¹(1/x)⁷ + ⁸C₈ x⁰(1/x)⁸

From the expansion, coefficient of x² is, ⁸C₃ and its value is,

⁸C₃ = 56

Example 3. Expand (x + 2)³

Solution:

Using Binomial Theorem:

(x + 2)³ = ∑ _k³₌₀ ( ³_k )x^3−k ⋅2^k

Calculate each term:

For k = 0:

( ³₀ ) x³⁻⁰⋅2⁰ = 1

For k = 1:

( ³₁) x³⁻¹⋅ 2¹ = 3⋅x²⋅2 = 6x²

For k = 2:

( ³₂ ) x³⁻² ⋅ 2² = 3 ⋅ x¹ ⋅ 4 = 12x

For k = 3:

( ³₃ ) x³⁻³ .2³ = 1 ⋅ x⁰ ⋅ 8 = 8

Combining Terms:

(x + 2)³ = x³ + 6x² + 12x + 8

Example 4. Use the binomial expansion to approximate (1.01)⁵

Solution:

We can rewrite (1.01)⁵ as (1 + 0.01)⁵

Using Binomial Theorem:

(1 + 0.01)⁵ = ∑ _k⁵₌₀ (⁵_k) (0.01) ^k

We can approximate this by using the first few terms (for simplicity, we’ll use up to k = 2):

For k = 0: (⁵₀) (0.01)⁰ = 1

For k = 1: ( ⁵₁) (0.01)¹=5 × 0.01 = 0.05

For k = 2: ( ⁵₂) (0.01)² = 10 × 0.0001 = 0.001

Approximate Sum:

(1 + 0.01)⁵ ≈ 1 + 0.05 + 0.001 = 1.051

Thus, (1.01)⁵ ≈ 1.051

Practice Questions on Coefficient in Binomial Expansion

Q1. Expand (3x − 2)⁴

Q2. Find the coefficient of x³ in the expansion of ( 2x + 5 )⁵.

Q3. Use the binomial expansion to approximate (1.02)⁶.

Q4. Calculate the binomial coefficient ( ⁷₃ ).

Q5. Identify the general term in the expansion of (x + 4y)⁶.

FAQs on Coefficient in Binomial Expansion

What is the relationship between binomial coefficients and Pascal’s Triangle?

Pascal’s Triangle shows the sum of the two numbers above determines each number. Binomial coefficients are found on the diagonals of the triangle, aiding in calculations.

What is Constant Term in the Binomial Theorem?

The constant term in a binomial expansion is determined by a numerical value independent of variables. To find the term not dependent on x in (x + y) ⁿ, locate the constant term.

Can Binomial Coefficients be Negative?

No, negative binomial coefficients are not possible. They are always non-negative integers since they represent counts or combinations.

Where is Binomial Theorem Used?

Binomial theorem is essential for expanding algebraic identities. Probability also utilizes this theorem for binomial expansion. Various algebraic identities can be derived using the binomial theorem.

• (a + b)² = a² + 2ab + b²
• (a – b)² = a² – 2ab + b²
• (a + b)(a – b) = a² – b²
• (a + b)³ = a³ +3a²b + 3ab² + b³
• (a – b)³ = a³ – 3a²b + 3ab² – b³
• (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac

Are Binomial Coefficients Same as Binomial Expansion Coefficients?

Yes, Binomial coefficients and binomial expansion coefficients represent coefficients in binomial equations, serving the same purpose in mathematics.