Level Order Traversal in C - Coding

The Level Order Traversal is a traversal technique used to traverse a tree level by level from top to bottom and from left to right at each level of a tree. In this article, we will learn how to implement level order traversal of a binary tree in C using two different methods.

Level order traversal of a Binary Tree

A binary tree is a hierarchical data structure where each node can have at most two children: a left child and a right child. Level order traversal allows us to process each node of the binary tree level by level from left to right. Generally, level order traversal is implemented using queues, but it can also be implemented without queues using recursion. Let’s look at an example to understand how level order traversal works.

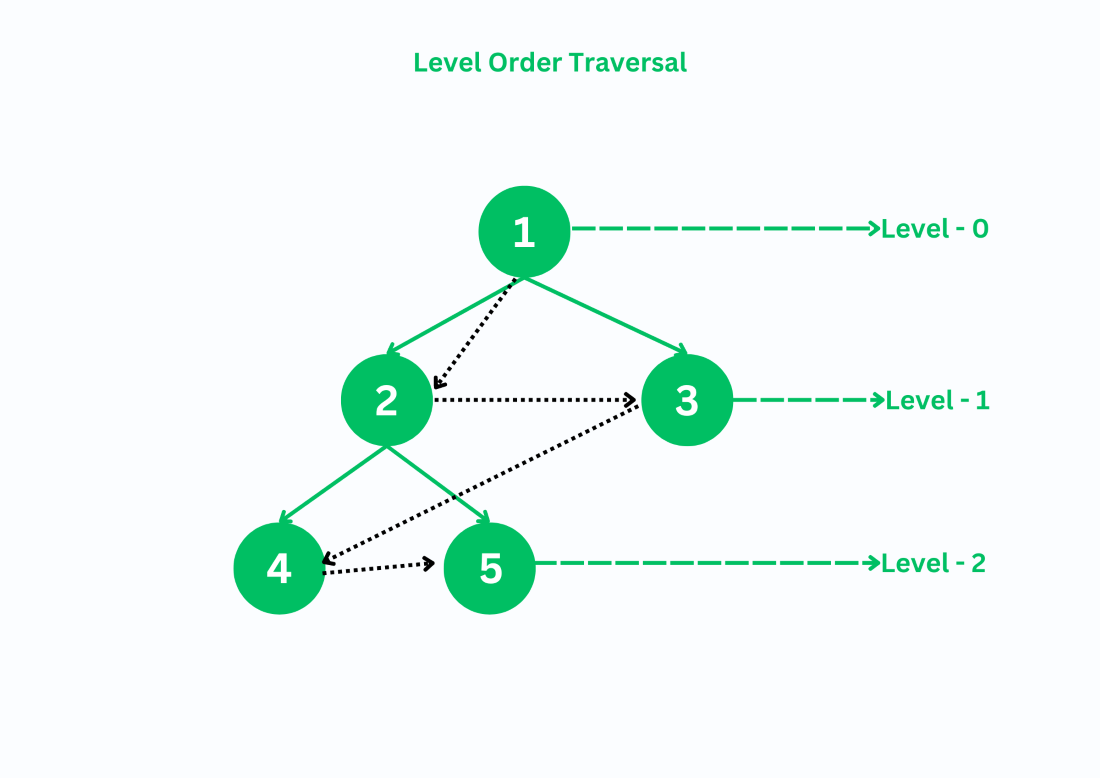Level Order Traversal in Tree

Implementation of Level Order Traversal in C

There are 2 methods through which we can implement the level order traversal of a tree in C. The methods are:

Recursive Method
Level Order traversal using queue.(Iteraive Method)

Recursive Level Order Traversal

To implement the recursive level traversal we can follow the below approach:

Approach

Define a function height to calculate the height of the tree.
Define a function printGivenLevel to recursively print nodes at a given level of the tree.
Iteratre through each level of the tree starting from 1 to calculated height.
Call the printGivenLevel function to print the nodes of that level.

C Program for Recursive Level Order Traversal

The following program illustrates how we can implement the recursive level order traversal for a tree in C:

// C Program for Recursive Level Order Traversal
#include <stdio.h>
#include <stdlib.h>

// Define the structure for a binary tree node
typedef struct Node {
    int data;
    struct Node* left;
    struct Node* right;
} Node;

// Function to find the maximum of two integers
int max(int a, int b) {
    return (a > b) ? a : b;
}
// Create a new tree node
Node* createNode(int data) {
    Node* newNode = (Node*)malloc(sizeof(Node));
    if (newNode) {
        newNode->data = data;
        newNode->left = NULL;
        newNode->right = NULL;
    }
    return newNode;
}

// Function to get the height of the tree
int height(Node* root) {
    if (root == NULL) return 0;
    int leftHeight = height(root->left);
    int rightHeight = height(root->right);
    return max(leftHeight,rightHeight) + 1;
}

// Function to print nodes of the tree at a given level
void printGivenLevel(Node* root, int level) {
    if (root == NULL) return;
    if (level == 1) printf("%d ", root->data);
    else if (level > 1) {
        printGivenLevel(root->left, level - 1);
        printGivenLevel(root->right, level - 1);
    }
}

// Function for level order traversal of the tree without using a queue
void levelOrderTraversal(Node* root) {
    int h = height(root);
    for (int i = 1; i <= h; i++) {
        printGivenLevel(root, i);
    }
}

// Example to demonstrate level order traversal without using a queue
int main() {
    // Create a simple binary tree
    Node* root = createNode(1);
    root->left = createNode(2);
    root->right = createNode(3);
    root->left->left = createNode(4);
    root->left->right = createNode(5);

    printf("Level Order Traversal:\n");
    // Perform the level order traversal on the tree without using a queue
    levelOrderTraversal(root);

    return 0;
}

Output

Level Order Traversal:
1 2 3 4 5

Time Complexity: O(N), where N denotes the number of nodes in the binary tree.
Auxiliary Space: O(1). The space complexity will be O(N) if the recusive stack space is considered. Because each recursive call adds a new frame to the call stack and if the recursion depth is proportional to the size of the input then the space complexity of the call stack will be O(N).

Level Order Traversal using Queue

We will follow the below approach to implement the level order traversal using queue:

Approach

Define the necessary data structure QueNode and Queue for implementing a queue which will be used for the level order traversal of the tree.
Create an empty queue.
Enqueue the root node of the tree to start the level order traversal process.
While the queue is not empty:
Dequeue a node from the front of the queue.
Print the value of the dequeued node.
Enqueue the node’s left child into the queue if it is present.
Enqueue the node’s right child into the queue if it is present.
Free the memory allocated for the queue.

C Program for Level Order Traversal using Queue

The following program demonstrates how we can implement the level order traversal of a binary tree using queue in C:

// C Program for level order traversal
#include <stdio.h>
#include <stdlib.h>

// Define the structure for a binary tree node
typedef struct Node {
    int data;
    struct Node* left;
    struct Node* right;
} Node;

// Define the structure for a queue node
typedef struct QueueNode {
    Node* treeNode;
    struct QueueNode* next;
} QueueNode;

// Define the structure for a queue
typedef struct Queue {
    QueueNode* front;
    QueueNode* rear;
} Queue;

// Create a new tree node
Node* createNode(int data) {
    Node* newNode = (Node*)malloc(sizeof(Node));
    if (newNode) {
        newNode->data = data;
        newNode->left = NULL;
        newNode->right = NULL;
    }
    return newNode;
}

// Create a new queue
Queue* createQueue() {
    Queue* queue = (Queue*)malloc(sizeof(Queue));
    if (queue) {
        queue->front = NULL;
        queue->rear = NULL;
    }
    return queue;
}

// Enqueue a tree node into the queue
void enqueue(Queue* queue, Node* treeNode) {
    QueueNode* newQueueNode = (QueueNode*)malloc(sizeof(QueueNode));
    if (newQueueNode) {
        newQueueNode->treeNode = treeNode;
        newQueueNode->next = NULL;
        if (queue->rear) {
            queue->rear->next = newQueueNode;
        } else {
            queue->front = newQueueNode;
        }
        queue->rear = newQueueNode;
    }
}

// Dequeue a tree node from the queue
Node* dequeue(Queue* queue) {
    if (queue->front) {
        QueueNode* temp = queue->front;
        Node* treeNode = temp->treeNode;
        queue->front = queue->front->next;
        if (!queue->front) {
            queue->rear = NULL;
        }
        free(temp);
        return treeNode;
    }
    return NULL;
}

// Check if the queue is empty
int isQueueEmpty(Queue* queue) {
    return queue->front == NULL;
}

//  Function for level order traversal of the tree
void levelOrderTraversal(Node* root) {
    if (root == NULL) {
        // if the tree is empty stop the program execution
        return;  
    }
    
    // Initialize a queue
    Queue* queue = createQueue();  
    // Enqueue the root node of the tree into the queue to start the traveral
    enqueue(queue, root);  
    
    // Continue the execution until all nodes of the tree are traversed
    while (!isQueueEmpty(queue)) {  
        // Get the front node from the queue
        Node* current = dequeue(queue);  
        // Print the node's value
        printf("%d ", current->data);  

        // Enqueue the childrens of the current node
        if (current->left) {
            enqueue(queue, current->left);
        }
        if (current->right) {
            enqueue(queue, current->right);  
        }
    }
    // Clean up the queue
    free(queue);  
}

// Example to demonstrate level order traversal
int main() {
    // Create a simple binary tree
    Node* root = createNode(1);
    root->left = createNode(2);
    root->right = createNode(3);
    root->left->left = createNode(4);
    root->left->right = createNode(5);

    printf("Level Order Traversal:\n");
    // Perform the level order traversal on the tree
    levelOrderTraversal(root);

    return 0;
}

Output

Level Order Traversal:
1 2 3 4 5

Time Complexity: O(N), where N denotes the number of nodes in the binary tree.
Auxiliary Space: O(N)

Reffered: https://www.geeksforgeeks.org

C Language

Related
Segment Tree in C
C Program to Implement Priority Queue
C Program to Implement Sieve of Eratosthenes
Bellman-Ford Algorithm in C
Implementation of B-Tree in C

Type:	Geek
Category:	Coding
Sub Category:	Tutorial
Uploaded by:	Admin
Views:	13