Rational numbers are numbers that can be expressed as a fraction of two integers, where the denominator is not zero. Some examples of rational numbers are 1/2, -3/2, 5, etc. 5 is whole number which can be written as 5/1 in the form of a fraction. Hence, we can say that a whole number is also a rational number.

In this article, we will understand the various properties of division of rational numbers and the procedure of division of rational numbers.

What are Rational Numbers?

Rational Number are the number that can be written in the form of p/q where p and q are integers and q is not equal to zero. Every fraction is considered to be a rational number, however every rational number is not a fraction. Rational number can be positive as well as negative.

Division of Rational Numbers

Division of rational numbers involves dividing one rational number (a number that can be expressed as a fraction) by another. In mathematical terms, when you divide one rational number a by another rational number b (where b is not zero), the result is also a rational number.

The division of rational numbers can be represented as follows:

a​/b ÷ cd ​= a/b ​× d/c​

Where:

• a/b is the dividend,
• c/d is the divisor,
• a/b ​÷ c/d is the quotient, and
• a/b × c/d​ is the equivalent multiplication expression.

How to Divide Rational Numbers

The steps to divide a rational number are:

Step 1: Express the rational number in fraction form.

Step 2: Next, write the first number as it is, and multiply by the reciprocal (the inverted form) of the divisor(second number).

Step 3: Multiply the numerators together and multiply the denominators together. This product of both numbers is called the division of rational number.

Let us now see these steps through an example. Suppose the given 2 rational numbers are 1/2 and 5

Step 1: Express the rational number in fraction form, here we have 1/2 and 5/1.

Step 2: The second number(divisor) is 5/1. Therefore, the reciprocal of 5 will be 1/5.

Step 3: Now the multiplication of both the fractions, so formed will be

= 1/2 × 1/5

= 1/10

= 0.1

Properties of Division of Rational Numbers

The properties of division of rational numbers are:

• Closure property
• Commutative property
• Associative property
• Property of 1
• Multiplicative Inverse

Let us understand each property in detail for better understanding.

Closure Property of Division of Rational Numbers

The closure property states that when one rational number is divided by another rational number (≠ 0), the result is not necessarily a rational number.

For example, 1/2÷1/3 = 3/2​ is a rational number. However, 1/3÷√2​ is not rational because √2​ is an irrational number. So, division of rational numbers does not always result in a rational number.

Commutative Property of Division of Rational Numbers

The commutative property states that changing the order of numbers in a division operation does not give the same result. In simple terms, if the numerator and denominators are swapped with each other then the result will not be same.

For rational numbers a and b, a÷b ≠ b÷a.

For example, 1/2 ÷ 1/3 ≠ 1/3 ÷ 1/2​. Thus, division is not commutative.

Associative Property of Division of Rational Numbers

For rational numbers a, b, and c, (a÷b)÷ c ≠ a÷(b÷c)

For example: The given numbers are 1/2, 1/3 and 1/4

Solution:

We have a= 1/2, b= 1/3, c= 1/4

[Tex](\frac{1}{2} \div \frac{1}{3}) \div \frac{1}{4} \neq \frac{1}{2} \div (\frac{1}{3} \div \frac{1}{4})[/Tex]

[Tex](\frac{3}{2}) \div \frac{1}{4} \neq \frac{1}{2} \div (\frac{4}{3})[/Tex]

[Tex](\frac{12}{2}) \neq (\frac{3}{8} )[/Tex]

[Tex]6 \neq (\frac{3}{8} )[/Tex]

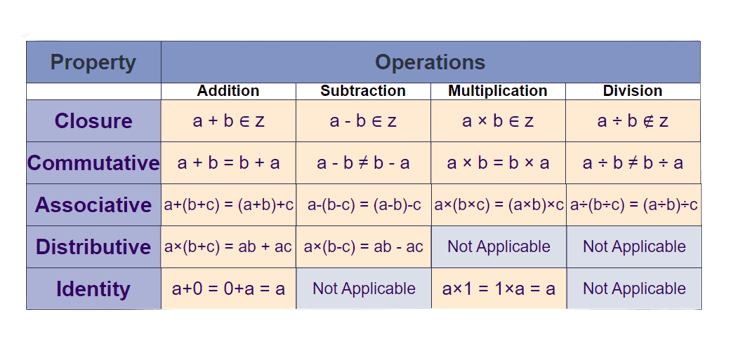
Property of 1 for Division of Rational Numbers

The property of 1 says that dividing any rational number by 1 leaves the number unchanged.

For any rational number a, a÷1 = a.

For example, 3/4 ÷ 1 = 3/4​. This property is true for all rational numbers.

Multiplicative Inverse

For any non-zero rational number a/b, the multiplicative inverse is b/a​. When the number is multiplied by its multiplicative inverse, the product is 1:

[Tex]\frac{a}{b} \times \frac{b}{a} = 1[/Tex]

Dividing two a rational number is equivalent to multiplying the first number by multiplicative inverse of the other number. If you need to divide m/n by p/q, you multiply m/n by the multiplicative inverse of p/q:

[Tex]\frac{m}{n} \div \frac{p}{q} = \frac{m}{n} \times \frac{q}{p}[/Tex]

Also Check,

• How to convert a rational number to a decimal?
• Rational and Irrational Numbers
• Properties of Rational Numbers

Solved Examples on Division of Rational Numbers

Example 1: Divide 3/4 by 2/5

Solution:

To divide 3/4​ by 2/5​, first multiply 3/4​ by the reciprocal of 2/5 that is 5/2​.

[Tex]\frac{3}{4} \div \frac{2}{5} = \frac{3}{4} \times \frac{5}{2}[/Tex]

= 15/8

Example 2: Divide 7/9 by 3.

Solution:

Given numbers are 7/9 and 3

We can write 3 as 3/1.

Now the reciprocal of 3/1 is 1/3

On multiplying numerator 7/9 by reciprocal 1/3 we get,

[Tex]\frac{7}{9} \div {3} = \frac{7}{9} \times \frac{1}{3}[/Tex]

= 7/27

Example 3: Evaluate 9/4 ÷ 3/2

Solution:

Given numbers are 9/4 and 3/2

Reciprocal of second number = 2/3

[Tex] \frac{9}{4} \div \frac{3}{2} [/Tex]

[Tex]= \frac{9}{4} \times \frac{2}{3} [/Tex]

[Tex]= \frac{9 \times 2}{4 \times 3} [/Tex]

= 18/12

= 3/2

Practice Questions on Division of Rational Numbers

Question 1. Divide 3/4 by 2/5

Question 2. Divide [Tex]\quad 2\frac{1}{3} \div 1\frac{1}{2}[/Tex]

Question 3. Divide 7/8 by 4

Question 4. Divide [Tex]\quad -\frac{5}{6} \div \frac{1}{3}[/Tex]

Question 5. Divide [Tex]\quad \left( \frac{7}{9} \div \frac{2}{3} \right) \div \frac{3}{4}[/Tex]

FAQs on Division of Rational Numbers

What is the rule in dividing positive and negative rational numbers?

On dividing the rational numbers if the signs of both numbers are same (both +ve or both -ve) then the result will be positive, while if the signs are different (one -ve and one +ve) then the result will be negative.

How do you divide rational numbers?

To divide rational numbers, multiply the first number by the reciprocal of the second number. The reciprocal is found by swapping the numerator and the denominator of the second number.

How do you divide rational numbers in fractional form?

To divide rational numbers in fractional form, multiply the first fraction by the reciprocal of the second fraction. For example, to divide a/b​ by c/d​, calculate a/b ​× d/c.

What is division of rational number called?

Division of rational numbers is called dividing rational numbers or rational division.

Is π a rational number?

No, π is not a rational number, as it cannot be expressed as a simple fraction of two integers.

Can we say whole numbers are rational numbers?

Yes, a whole number is a rational number. This is because any whole number can be expressed as a fraction with a denominator of 1. For example, the whole number 3 can be written as 3113​, which is a rational number.