Finding the range of a function is an essential skill in algebra that involves determining all the possible output values (y-values) that a function can produce. While graphing the function can provide a visual representation of the range, finding the range algebraically offers a more precise and analytical approach. This method is particularly useful when dealing with complex functions where graphing may not be straightforward. In this article, we will explore various algebraic techniques to determine the range of different types of functions, such as linear, quadratic, rational, exponential, and trigonometric functions.

What is the Range of a Function?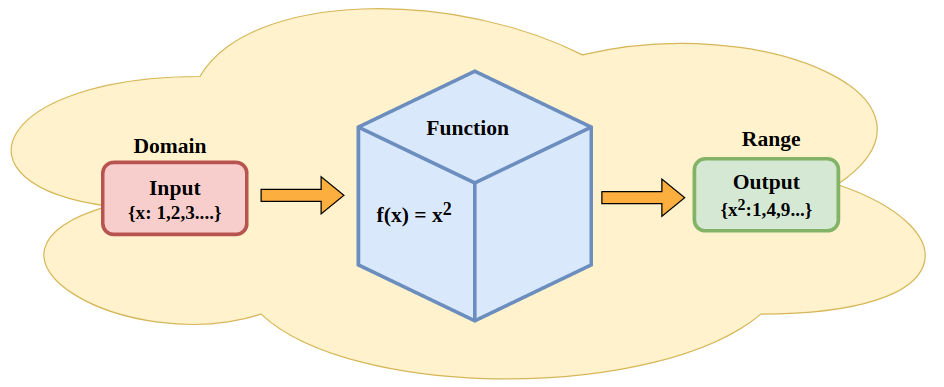

The range of a function is the set of all possible output values (y-values) that the function can produce. In other words, it represents all the values that f(x) can take when x varies over the entire domain of the function.

For example, if you have a function f(x), the range is the collection of all values f(x) such that x is within the domain of f. Determining the range involves understanding the behavior of the function, its equations, and any constraints or limits on the values it can output.

The range provides critical information about the function’s scope and behavior, helping to understand its potential outputs and how it maps inputs to outputs. Different types of functions (linear, quadratic, rational, etc.) have different methods for finding their ranges, but the concept remains the same: it is all about identifying the possible outputs based on the given inputs.

Types of Functions

Linear Functions

A linear function is a polynomial of degree one with a graph represented by a straight line.

General Form: f(x) = mx + b

Where:

• m is the slope
• b is the y-intercept

Example: f(x) = 2x + 3

Range:

The range of a linear function is all real numbers, R.

Quadratic Functions

A quadratic function is a polynomial function of degree 2. Its graph is a parabola that opens either upwards or downwards.

General Equation: f(x) = ax² + bx + c, where ???? ≠ 0 .

Example: f(x) = x² − 4x + 4

Range:

• If a > 0, the parabola opens upwards, and the range is [minimum value, ∞)[minimum value, ∞).
• If a < 0, the parabola opens downwards, and the range is (−∞, maximum value](−∞, maximum value].

For f(x) = x²−4x+4:

• Vertex form: f(x) = (x−2)²
• Minimum value at x = 2 is f(2) = 0.
• Range: [0, ∞)[0, ∞)

Rational Functions

A rational function is a function that can be expressed as the ratio of two polynomials.

General Form: f(x) = q(x) / p(x)​, where p(x) and q(x) are polynomials and ????(????) ≠ 0

Example: ????(????) = 1 / x − 1

Range:

The range of a rational function depends on the specific function and its asymptotes.

For f(x) = 1 / (x-1)​, the range is R∖{0}.

Exponential Functions

An exponential function has a consistent base but changes in the exponent.

General Form: f(x) = a ⋅ b ^x , where ???? ≠ 0 b > 0, and ???? ≠ 1

Example: f(x) = 2 ^x

Range:

The range of an exponential function is all positive real numbers, (0, ∞).

Trigonometric Functions

Trigonometric functions are functions that relate the angles of a triangle to the lengths of its sides. The most common trigonometric functions are sine, cosine, and tangent.

General Form:

• Sine: f(x) = sin(x)
• Cosine: f(x) = cos(x)
• Tangent: f(x) = tan(x)

Example: f(x) = sin(x), f(x) = 3cos(2x− 4/π) + 1

Range:

• Sine and Cosine: The range is [−1, 1][−1, 1].
• Tangent: The range is all real numbers, R, except where the function is undefined (at x = π​/2 + kπ for any integer k).

Steps to Find the Range Algebraically

Identify the Function: Define function f(x) to find its range.

Solve for the Dependent Variable: Express the function in terms of dependent variable y; solve for x in terms of y by setting y = f(x).

Analyze the Inverse Function: Determine if the inverse function x = f⁻¹(y) is real by solving the equation y = f(x) for x.

Consider the Domain of the Inverse Function: The inverse function f⁻¹(y) will have a domain that matches the range of the original function f(x), ensuring compatibility between x and y values.

Identify Any Constraints: Consider restrictions such as square roots being non-negative and denominators not equaling zero in functions.

Example of finding the range:

Linear Function f(x)=2x+3

Identify the function: f(x) = 2x + 3.

Set y = 2x + 3 and solve for x:

y = 2x + 3 ⟹ x = (y − 3) / 2

​Since there are no restrictions on y, the range is all real numbers.

Range: R.

Graphical Interpretation of Range

This can be done by examining the graph of the function systematically.

• Graph the Function: Plot function accurately by including main points and features such as intercepts, asymptotes, and distinctive characteristics on graph.

• Observe the Vertical Extent: Analyzing the graph vertically aids in observing the range of y-values accepted by the function, facilitating easier observation.

• Identify Asymptotes and Discontinuities: Identify horizontal asymptotes and note their approach. Find vertical asymptotes and discontinuities affecting the range, like gaps or holes.

• Find the Minimum and Maximum Values: Identify graph’s lowest and highest points to determine range boundaries for useful information purposes.

• Include All Possible Outputs: Consider all y-values attained by a function, even if it approaches values asymptotically.

Visualizing the function’s behavior

Visualizing a function’s range, scope, and general features can improve understanding. Follow these procedures and advice to better comprehend the behavior of different function types.

• Plot Key Points: The intercepts where the function intersects the y and x-axes are located and plotted. More points can be computed and plotted to better understand the function’s form.

• Identify Asymptotes: Find asymptotes of exponential and rational functions by determining vertical and horizontal lines. Plot them as dashed lines for reference.

• Determine Symmetry: The examination of f(−x) can determine if a function is even, odd, or neither based on visual patterns of symmetry about the origin or y-axis.

• Analyze End Behavior: Analyze function behavior at infinity; determine if approaching asymptote, increasing, or decreasing.

• Check for Extrema: The first derivative helps identify local maxima, minima, and critical points for polynomial and smooth functions, aiding in understanding peaks and valleys within a given interval.

• Understand Periodicity: Identify phase, amplitude, and period alterations for trigonometric functions to understand recurring patterns.

Solved Problems on Range of a Function

Problem 1. Find the range of the rational function ????(????) = x² −2 / x-2 .

Solution:

Step 1: Identify the Rational Function:

• The given function is ????(????) = x²−2 / x-2 .

Step 2: Determine the Domain:

• The domain of a function includes all real integers except 0 in the denominator.
• When x=2, x-2=0, so x=2 is an exception to the domain.

Step 3: Analyze Vertical Asymptotes:

• Because the denominator drops to zero at x=2, the function exhibits a vertical asymptote. When x approaches 2 from the left or right, the function behaves as 1/x−2, approaching positive or negative infinity, respectively, near x=2.

Step 4: Analyze Horizontal Asymptotes:

Compare degrees of numerator and denominator polynomials for horizontal asymptotes; both degree 1 means no existent asymptote.

Step 5: Consider End Behavior:

The function acts like ????² / x as x approaches positive or negative infinity, and as x gets big, it simplifies to x. Therefore, the range has no upper or lower bound.

Step 6: Combine Results:

The function approaches positive or negative infinity as x approaches 2 due to the absence of horizontal asymptotes and the presence of a vertical asymptote at x=2.

Step 7: Express the Range:

Except for any values that the function is unable to reach because of domain limitations, the range is all real numbers as the function approaches positive or negative infinity without bound as x approaches 2. Since x cannot equal 2, the range in this instance is (−∞,+∞), omitting f(2).

So, the range of the function ????(????)=????²−1???? /x – 2 is (−∞,+∞) excluding f(2).

Problem 2. Find the range of the quadratic function ????(????)=x²−4x+3.

Solution:

Step 1: Determine the Function:

The quadratic function f(x)=x²−4x+3 is equal to ???? (???? )²−4???? + 3.

Step 2: Determine the Domain: Any polynomial function has real numbers as its domain.

Step 3: Analyze Critical Points: x = -b/2a = 4/2(1) = 2

Step 4: Determine the Vertex: Substitute x = 2x into the function:

f(2) = 2² – 4(2) + 3 = 4 – 8 + 3 = -1

So, the vertex is at (2,−1).

Step 5: Consider End Behavior: Since the leading term x² controls the behavior of the function, f(x) likewise tends toward positive infinity when x approaches positive or negative infinity.

Step 6: Express the Range: Since the quadratic function

????(????)=????²−4????+3

f(x)=x²−4x+3 opens upwards (because ????>0), the minimum value occurs at the vertex (2,−1).

Therefore, the range is all real numbers greater than or equal to −1, or in interval notation, (−1,+∞).

Problem 3. How to find the range of a modulus function f(x) = |x − 1 |.

Solution:

f(x) = 1 – |x − 3 |

It is clear that Domain = R defines it for all values of x.

Right now,

y = 1 − | x − 3 |

| x − 3 | = 1 − y

Undoubtedly, given actual of x, 1 − y > 0 or y = 1.

The range is thus (−∞, 1 ]

Analogously, we determine the range of many functions algebraically, that is, without creating a graph. (How to determine a function’s range without graphing)

Problem 4. Find the range of the quadratic function f (x) = x² − 4x + 3.

Solution:

Step 1: Identify the function: The given function is f(x)=x² − 4x + 3 which is a quadratic function.

Step 2: Determine the domain: The domain of every polynomial function is a real number.

Step 3: Analyze the critical points: To find the critical points, we find the peak of the quadratic function. The vertex of the quadratic function f(x)=ax² + bx + c (h, k) is given by the formula h = − b / 2a and k = f(h).

If f(x) = x² − 4x + 3: ℎ=−???? / 2????

=−4/2(1) = 2

Step 4: Determine the vertex : Substitute x=2 in the function to find the correspondingly-coordinate:

f(2) = (2)²− 4(2) + 3 = 4 − 8 + 3 = −1 , So the vertex is ( 2,−1).

Step 5: Consider finite behavior: As x approaches positive or negative infinity ,f(x) also tends to positive infinity because the behavior of the function is governed by the leading term x².

Step 6: Expression of the interval:

Since the quadratic function

f(x) = x² − 4x +3 opens (because a>0), the minimum value occurs at the vertex (2, −1). Therefore, the interval is all real numbers greater than or equal to -1 or with space notation (-1,+∞).

So the interval of the quadratic function f(x) = x² − 4x + 3 is (−1,+∞).

Problem 5 . Find the range of the quadratic function f(x) = 1 / x

Solution:

The function g(x) = 1 / x is analyzed to determine its domain, vertical asymptotes, final behavior, and range.

Given the function f(x) = 1/x.

Step 1: Identify the domain

The function is not defined at x = 0.

Domain: R \ {0}.

Step 2: Analyze the behavior of the function

[Tex]x \to +\infty, \frac{1}{x} \to 0^+.[/Tex]

[Tex]x \to -\infty, \frac{1}{x} \to 0^-.[/Tex]

Step 3: Analyze near the origin

[Tex]x \to 0^+, \frac{1}{x} \to +\infty.[/Tex]

[Tex]x \to 0^-, \frac{1}{x} \to -\infty.[/Tex]

Step 4: Determine the possible values of f(x)

f(x) can take any positive value for very small positive x.

f(x) can take any negative value for very small negative x.

Conclusion

f(x) can be any real number except 0.

Range: (-∞, 0) ⋃ (0, +∞)

Common Functions and Their Ranges