
|
|
Pascal’s triangle is a triangular array of binomial coefficients. Each number in the triangle is the sum of the two directly above it. Given a non-negative integer N, the task is to find the Nth row of Pascal’s Triangle. 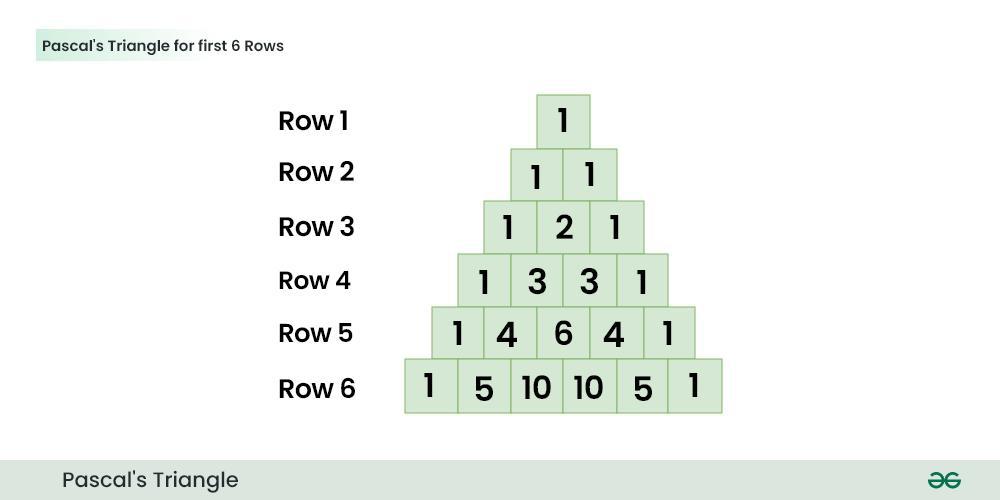 Table of Content Using Binomial Coefficient FormulaThis approach relies on the binomial coefficient formula to compute the value of each element in the nth row of Pascal’s triangle. The binomial coefficient formula calculates the number of ways to choose k elements from a set of n elements denoted as “C(n, k)”. The formula for binomial coefficient is: C(n, k) = n! / (k! * (n - k)!)Example: This example prints the n-th row of Pascal’s triangle using binomial coefficient formula. Output [ 1, 3, 3, 1 ] Time Complexity: O(N2) Space Complexity: O(N) Using RecursionThis approach uses recursion to generate the nth row of Pascal’s triangle. Here each element in a row (except the first and last elements which are always 1) is computed by summing the two elements diagonally above it in the previous row. Example: This example uses recursion to print the n-th row of Pascal’s triangle. Output [ 1, 4, 6, 4, 1 ] Time Complexity: O(2n) due to recursion Space Complexity: O(n) |
Reffered: https://www.geeksforgeeks.org
| JavaScript |
Type: | Geek |
Category: | Coding |
Sub Category: | Tutorial |
Uploaded by: | Admin |
Views: | 18 |