To find the maximum and minimum values of a function we find the derivatives of the given function. If the function f(x) ≤ f(a) for all x ∈ D then f(a) is the maximum value of the function and if f(x) ≥ f(a) for all x ∈ D then f(a) is the minimum value of the function.

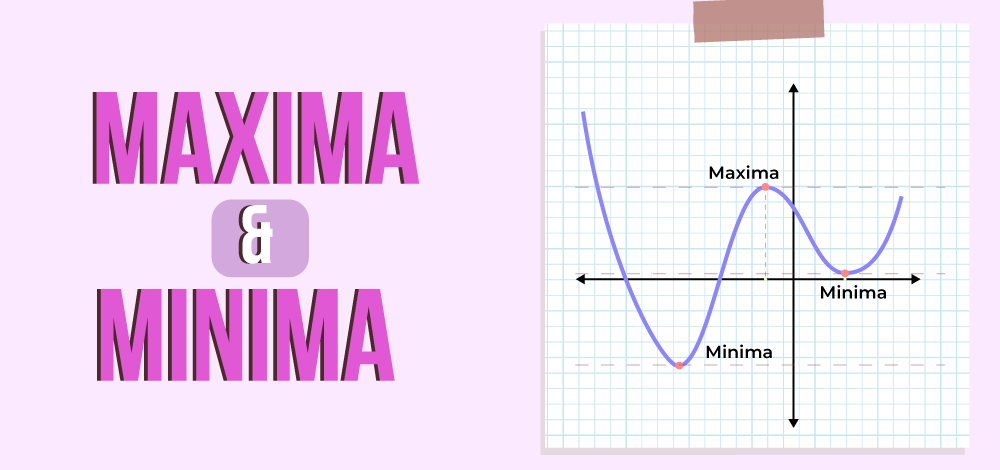
In this article, we will explore how to find the minimum and maximum values of a function along with the maximum and minimum function definitions and conditions, and steps to find the maximum and minimum values of a function.

What is Function in Mathematics?

Functions is a rule that assigns one element of a set to each element of other sets. It is represented as f: X→ Y where X is called the domain of the function and Y is called the co-domain of the function.

What is Maximum Value of Function?

Maximum value of the function is the value at a point for which the function obtains its maximum value. In other words, if the function f(x) ≤ f(a) for all x ∈ D then f(a) is the maximum value of the function.

Maximum and Minimum value of ay function is calculated below:

Condition for Maximum Value of Function

Conditioan at x = a maximum of f(x) exist is,

f(x) ≤ f(a) for all x ∈ D

f(a) is the maximum value of the function.

What is Minimum Value of Function?

Minimum value of function is the value at a point for which the function obtains its minimum value. In other words, if the function f(x) ≥ f(a) for all x ∈ D then f(a) is the minimum value of the function.

Condition for Minimum Value of Function

Conditioan at x = a minimum of f(x) exist is,

f(x) ≥ f(a) for all x ∈ D

f(a) is the minimum value of the function.

Steps to Find Maximum and Minimum Values of Function

Steps to find the maximum and minimum value of the function are added below:

• Step 1: Find the first derivative of the function.

• Step 2: Equate the first derivative of function to 0.

• Step 3: Find the critical points from the above expression.

• Step 4: Find the second derivative of the function.

• Step 5: If by putting the critical point in the second derivative if the resultant value is negative then, it is point of maxima and if the resultant value is positive then, it is point of minima.

• Step 6: By substituting the values of maxima and minima points we get the maximum value and minimum value of the function.

This is further explain with the help of an example added below:

Example: Find maximum and minimum of function y = x³ – 3x + 11

Solution:

y = x³ – 3x + 11

Find first order derivative. Differentiating y

y’ = (d / dx) [x³ – 3x + 11]

⇒ y’ = (d / dx) x³ – (d / dx) (3x) + (d / dx) 11

⇒ y’ = 3x² – 3 + 0

⇒ y’ = 3x² – 3

Now equate y’ = 0, to find the critical points

y’ = 0

⇒ 3x² – 3 = 0

⇒ 3x² = 3

⇒ x² = 1

⇒ x = 1 or x = -1

Critical points are x = 1 and x = -1

Now we will find second derivative to check the critical point is maxima or minima.

y” = (d / dx) [3x² – 3]

⇒ y” = (d / dx) [3x²] – (d /dx) [3]

⇒ y” = 6x – 0

⇒ y” = 6x

Now we will put the values of x and find whether y” is greater than 0 or less than 0.

At x = 1

y” = 6(1) = 6

Since, y” > 0 x = 1 is the minima of y

At x = -1

y” = 6(-1) = -6

Since, y” < 0 x = -1 is the maxima of y

• Maximum of y at x = -1 is, (-1)³ -3(-1) + 11 = -1 + 3 + 11 = 13
• Minimum of y at x = 1 is, (1)³ -3(1) + 11 = 1 – 3 + 11 = 9

Examples of Finding Maximum and Minimum Value of a Function

Example 1: Find the maximum and minimum value of a function f(x) = x³ + 8x² + 16x + 2.

Solution:

f(x) = x³ + 8x² + 16x + 2

First, find f'(x)

f'(x) = 3x² + 16x + 16

Then, equate f'(x) = 0, to find critical points.

3x² + 16x + 16 = 0

3×2 + 12x + 4x + 16 = 0

3x (x + 4) + 4 (x + 4) = 0

(x + 4) (3x + 4) = 0

x = -4, -4/3

Then, find f”(x) of given function

f”(x) = 6x + 16

Put critical points in f”(x) to find the point of maximum and minimum.

x = -4, f”(x) = -8

x = -4/3, f”(x) = 8

Since, the value is negative for x = -4 so, it is point of maximum and the value is positive for x = -4/3 so it is point of minimum.

Then, put these values in the f(x) to find the maximum and minimum value of the function.

Maximum value = f(-4) = – 94

Minimum value = f(-4/3) = -202 /27 = -7.48

Example 2: Find the maximum and minimum value of a function g(x) = (x³ )/3 – (x² )/2 – 6x +2

Solution:

f(x) = (x³)/3 – (x²)/2 – 6x +2

First, find f'(x)

f'(x) = x² – x – 6

Then, equate f'(x) = 0, to find critical points.

x² – x – 6 = 0

x² – 3x + 2x – 6 = 0

x (x – 3) + 2 (x – 3) = 0

(x + 2) (x – 3) = 0

x = -2, 3

Then, find f”(x) of given function

f”(x) = 2x – 1

Put critical points in f”(x) to find the point of maximum and minimum.

x = -2, f”(x) = -5

x = 3, f”(x) = 5

Since, the value is negative for x = -2 so, it is point of maximum and the value is positive for x = 3 so it is point of minimum.

Then, put these values in the f(x) to find the maximum and minimum value of the function.

Maximum value = f(-2) = 28/3

Minimum value = f(3) = -23/2

Practice Questions of Maximum and Minimum Value of a Function

Q1. Find the maximum and minimum value of a function p(x) = x⁴ + 3x³ + 4x² + 2x + 5.

Q2. Find the maximum and minimum value of function g(x) = x³ + 9x² + 3x + 12

Q3. Find the maximum and minimum value of a function q(x) = 2x³ + 3x² + 8x + 10

FAQs on Finding Maximum and Minimum Value of a Function

How to Find Maximum and Minimum Value of a Function?

To find the maximum and minimum value of the function we follow below steps.

• Find first derivative of given function and equate it to 0.
• Then, find the critical points from the above equation.
• Find the second derivative of function.
• To identify the point of maximum and minimum put values of critical points in second derivative and find its value.
• If the value is negative the point is point of maximum and if the value is positive it is point of minimum.
• Then, substitute the point of minimum and maximum in the function to get the maximum and minimum value of the function.

What is the Condition of the Maximum Value of a Function?

The condition for maximum value of a function is:

f(x) ≤ f(a) for all x ∈ D

f(a) is the maximum value of function

What is the Minimum Value of a Function?

The minimum value of the function is the minimum value a function can obtain.