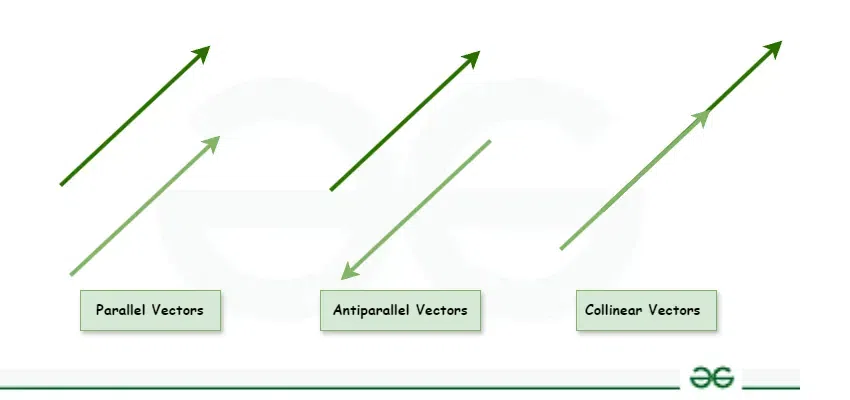
Parallel vectors are considered one of the most important concepts in vector algebra. When two vectors have the same or opposite direction, they are said to be parallel to each other. Note that parallel vectors can differ in magnitude, and two parallel vectors can never intersect each other. They are widely used in mathematics, physics, and other areas of engineering for defining lines and planes, representing force and velocity, and analyzing various structures.

In this article, we will learn about parallel vectors, the dot product, and the cross product of parallel vectors, as well as their properties, in detail.

What are Parallel Vectors?

Parallel vectors are vectors that have the same or opposite direction. When the angle between two vectors is 0° or 180°, then the vectors are said to be parallel vectors.

Parallel vectors may or may not differ in magnitude. Sometimes, when the angle between two parallel vectors is 180°, they are also referred to as antiparallel vectors. Parallel vectors are also known as collinear vectors because they lie on the same or parallel lines.

How to Find Parallel Vectors ?

If two vectors are parallel to each other they can be represented as scaler multiple of one another i.e. we can say that the given two vectors X and Y are parallel, if there exists a unique number ‘k’ such that:

X = k × Y

where k can be positive, negative or zero.

• If k is positive then the vectors are parallel and in the same direction.
• If k is negative then the vectors are parallel and in opposite direction or they are antiparallel to each other.

Unit Vector parallel to Given Vector

Unit vectors is a vector whose magnitude is one unit. Unit vector parallel to the given vector is the vector whose magnitude is one and in the same direction as given vector. To find unit vector parallel to the given vector divide the given vector with its magnitude as

â = a / |a|, where |â|=1

Therefore, the vector â is a unit vector parallel to given vector a, obtained by dividing the given vector a with its own magnitude.

Dot Product of Parallel Vectors

Dot product is the product of magnitude of the two vectors with cosine of the angle between the two vectors. For parallel vectors the angle between the two vectors is 0°. So dot product of parallel vectors is simply the product of their magnitudes.

By definition of dot product of two vectors we know that,

a.b =|a| |b| cosθ

As angle between parallel vectors is zero,

a.b = |a| |b| cos0

a.b = |a| |b| (1)

a.b = |a| |b|

Hence it is proved that the dot product of two parallel vectors is the product of their magnitudes.

Cross Product Of Parallel vectors

Cross product or vector product is the product of magnitude of the vectors with the sine of angle between the two vectors. Since parallel vector have angle 0° between them, So cross product of parallel vectors is zero.

From the definition of cross product we know,

a×b =|a| |b| sinθ Û .

Here Û represent the unit vector in the direction of a×b.

a×b = |a| |b| sin0 Û .

a×b = |a| |b| (0) Û .

a×b = 0

Hence it is proved that he cross product of two parallel vectors is always zero.

Properties of Parallel Vectors

Some of the Important properties of Parallel vectors are as below:

• Every vector is parallel to itself and antiparallel to its opposite.

• Parallel vector lie on the same or parallel lines.

• Cross product of parallel vectors is always zero.

• Sum of two parallel vectors is also a parallel vector.

• Dot product of two parallel vectors is equal to the product of their magnitudes.

• Two vectors are parallel if they can be represented as scalar multiple of one another.

Sample Problems on Parallel Vector

Example 1: Verify whether the vectors are parallel , antiparallel or intersecting U=3i + 2j -k and 3V =i + 2j – k.

Solution:

For vector U, the direction vector [Tex]\vec{u}[/Tex] is <3, 2, -1>.

For vector V, the direction vector [Tex]\vec{v}[/Tex] is <1, 2, -1>.

Comparing the direction vectors, we see that [Tex]\vec{u}[/Tex] and [Tex]\vec{v}[/Tex] are not scalar multiples of each other, nor are they negatives of each other.

Hence, U and V are neither parallel nor antiparallel. They intersect at some angle.

Example 2: Find a Unit Vector parallel to given vector U = 3i + 4j + 12j?

Solution:

Unit vector parallel to given vector can be found by dividing the given vector with it own magnitude as:

Given U = 3i + 4j + 12j ,

|U| = √3² + 4² +12²

= √9 + 16 + 144 = √169 = 13

So Unit vector parallel to given U vector is = (3i + 4j + 12k ) / 13

Example 3: Find the dot and cross product of the vectors U = 3i + j -2k and U = 6i +2j – 4k?

Solution:

Given,

U = 3i + j -2k

V = 6i + 2j – 4k

It can be seen that V = 2U

So we can say that both the vectors are parallel to each other.

Dot product : For parallel vector U.V = |U| |V|

or |U|=√3² + 1² +2² = √9 + 1 + 4 = √14

|V| = √6² +2² + 4² = √36 + 4 + 16 = √56

So U.V = √14 ×√56= √784 = 28.

Cross Product : The cross of two parallel vectors is zero.

Example 4: Find a vector parallel to the vector U = 3i + 4j and has magnitude twice the magnitude of U?

Solution:

Given vector U = 3i + 4j.

Magnitude of U, |U| = √(3² + 4²) = 5.

A vector parallel to U with twice the magnitude: V = 2U = 6i + 8j.

Magnitude of V, |V| = √(6² + 8²) = 10.

FAQ on Parallel Vector

What are parallel vectors?

Parallel vectors are vectors that always have the same or opposite directions but can have different magnitudes.

Can parallel vectors be called collinear vectors?

Yes, parallel vectors can be called collinear vectors when they lie along the same line or when they can be represented by the same line.

Do parallel vectors always have the same starting and ending points?

No, parallel vectors do not need to start and end at the same point. They can have different starting and ending points, such as 3i and 8i, which are parallel to each other.

Is there any vector parallel to every other vector?

Yes, the zero vector (with each part being zero, i.e., 0i + 0j + 0k) is considered parallel to every other vector.

Why is every vector parallel to itself?

Every vector is parallel to itself because every vector can be written as a scalar multiple of itself, e.g., a = 1×a.

Are parallel vectors and equal vectors the same?

No, parallel vectors and equal vectors are two different entities. Equal vectors always have the same magnitude and direction, whereas parallel vectors may or may not have equal magnitudes and can be in the same or opposite directions.