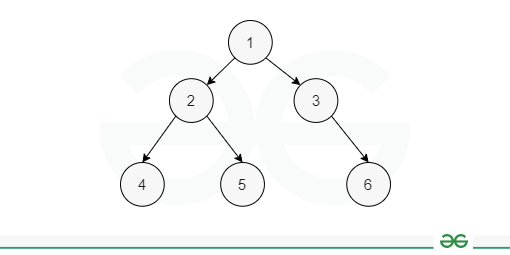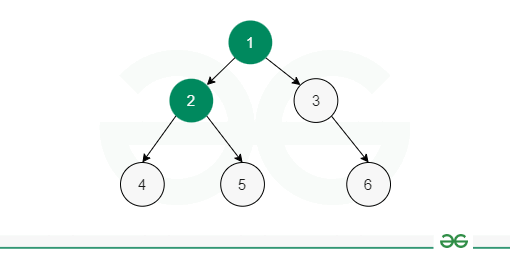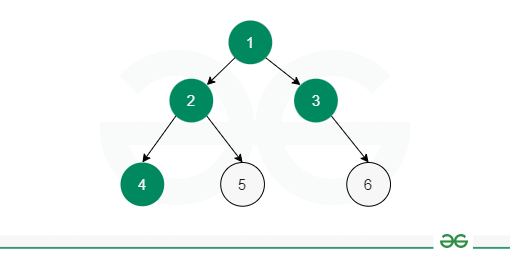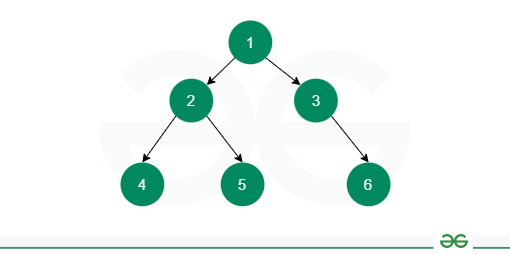
Trees are the type of data structure that stores the data in the form of nodes having a parent or children or both connected through edges. It leads to a hierarchical tree-like structure that can be traversed in multiple ways such as —preorder, inorder, postorder, and level order. A binary tree is a tree data structure a node can only have 2 children at max.

In this article, we will learn about level order binary tree traversal in C++, how to implement it using a C++ program and analyze its time and space complexity.

Level Order Traversal of Binary Tree in C++

The level order traversal is a type of Breadth First Traversal (BFS) in which we traverse all the nodes in the current level and then move to the next level. It starts from the root level and goes to the last level. Consider the below example:

            1
          /  \
        2      3
     /   \       \
   4      5       6

The level order traversal of the given tree will be: 1 2 3 4 5 6

Level Order Binary Tree Traversal

Algorithm for Level Order Binary Tree Traversal in C++

There are multiple methods to implement level order traversal in C++ Level order traversal can be implemented using a queue data structure. The process is as follows:

• Start by pushing the root node into the queue.
• While the queue is not empty, repeat the following steps:
  • Dequeue the node from the front of the queue.
  • Visit the node (typically, process or print the node’s value).
  • Enqueue the left child of the node if it exists.
  • Enqueue the right child of the node if it exists.

C++ Program to Implement Level Order Tree Traversal

Here is a simple C++ program that demonstrates the level order traversal of a binary tree:

// C++ program to illustrate how to implement
#include <iostream>
#include <queue>
using namespace std;

// treenode
struct Node {
    int data;
    Node* left;
    Node* right;
    Node(int value): data(value),
    left(nullptr), right(nullptr){}
};

// function for level order traversal
void levelOrderTraversal(Node* root)
{
    // checking if the tree is empty or not
    if (root == nullptr)
        return;

    // creating and initializing queue with root as first
    // element
    queue<Node*> q;
    q.push(root);

    // loop that will run till the q is empty
    while (!q.empty()) {

        // visiting current node which is nothing but
        // q.front()
        Node* node = q.front();
        q.pop();
        cout << node->data << " ";

        // pushing left child and rightchild if they exists.
        if (node->left != nullptr)
            q.push(node->left);
        if (node->right != nullptr)
            q.push(node->right);
    }
}

// driver code
int main()
{
    Node* root = new Node(1);
    root->left = new Node(2);
    root->right = new Node(3);
    root->left->left = new Node(4);
    root->left->right = new Node(5);
    root->right->right = new Node(6);

    cout << "Level Order Traversal of Binary Tree: ";
    levelOrderTraversal(root);
    return 0;
}

Level Order Traversal of Binary Tree: 1 2 3 4 5 6 

Complexity Analysis of Level Order Binary Tree Traversal in C++

This is the analysis of the level order traversal algorithm that uses the queue data structure.

Time Complexity

In the while loop, we are pushing each node in the queue, processing it once and popping it. Every node in the tree will be pushed in the queue once. So,

Time Complexity of the level order binary tree traversal using queue is O(N)

where N is the total number of nodes in the tree.

Auxiliary Space Complexity

When we are at the root node, we push the root->left and root->right in the queue. When we are at the root->right, we have already pushed both children of the root->left and we push both the children of root->right. This infers that whenever we are at the rightmost node of the current level, all the nodes of the next level (i.e. the respective children’s of all the nodes in the current level) and we know that the maximum possible number of of nodes are in the lowest level.

Best Case: Skew/Degenerate Binary Tree

The best case for the space complexity will be skew/degenerate binary tree as they have only one node at every level. So, for skew/degenrate trees,

Auxiliary Space Complexity: O(1)

Wrost Case: Perfect Binary Tree

In perfect binary tree, the number of nodes in the lowest level is N/2, where N is the total number of nodes. So, for perfect or even full and complete binary tree,

Auxiliary Space Complexity: O(N)

Level Order Traversal without a Queue: Recursive Approach

In this approach, you essentially use a recursive function to visit nodes level by level and store the node values in the 2D vector where the row corresponds to the level and the columns are the nodes in the level.

Algorithm

This methods requires two functions, one is the recursive function that takes the reference to the tree and the 2D vector and insert the nodes in the array at corresponding rows and the other is the one which calls this recursive function and then prints the level order.

Recursive Function

• This function takes the pointer to the node, current level and the reference to the 2D vector.
• First, we check if the current node is NULL. If it is NULL, we return to the caller. Otherwise.
• Push the current node value to that row of 2D vector which is equal to the current level.
• Then, call this function for node->left with level = level + 1.
• Again call this function for node->right with level = level + 1.

Calling Function

• First check if the tree is empty or not. If not then
• Create a 2D vector for storing the level order values.
• Call the recursive function and pass the reference to this vector.
• Print the vector.

C++ Program to Implement the Level Order Binary Tree Traversal without Queue

// C++ program to demonstrate how to implement the level
// order traversal without using queue
#include <iostream>
#include <vector>
using namespace std;

// tree noode
struct TreeNode {
    int val;
    TreeNode *left, *right;
    TreeNode(int x): val(x), left(NULL), right(NULL){}
};

// recursive function as level order traversal helper
// function
void levelOrderHelper(TreeNode* node, int level,
                      vector<vector<int> >& results)
{
    if (!node)
        return;
    // Ensure the vector is large enough to include this
    // level
    if (level == results.size())
        // Add a new level
        results.push_back(vector<int>());
    // pushing current node value
    results[level].push_back(node->val);

    // Recurse to the left and right, increasing the level
    levelOrderHelper(node->left, level + 1, results);
    levelOrderHelper(node->right, level + 1, results);
}

// parent level order traversal function
void levelOrderTraversal(TreeNode* root)
{
    // creating vctor to store result
    vector<vector<int> > results;

    // calling helper function
    levelOrderHelper(root, 0, results);

    // printing level order
    for (const auto& level : results) {
        for (int val : level) {
            cout << val << " ";
        }
    }
}

int main()
{
    // Create nodes
    TreeNode* root = new TreeNode(8);
    root->left = new TreeNode(3);
    root->right = new TreeNode(10);
    root->left->left = new TreeNode(1);
    root->left->right = new TreeNode(6);
    root->right->right = new TreeNode(14);
    root->left->right->left = new TreeNode(4);
    root->left->right->right = new TreeNode(7);
    root->right->right->left = new TreeNode(13);

    // Perform level order traversal without a queue
    cout << "Level order traversal output:\n";
    levelOrderTraversal(root);

    return 0;
}

Level order traversal output:
8 3 10 1 6 14 4 7 13 

Complexity Analysis of Level Order Binary Tree Traversal

Although this method works differently from the queue method, the time and space complexity of this method is same as that of the queue method.

Time Complexity

In the above program, we start from the root node and then go to the left and right child using recursion. This goes on till we find the NULL. It shows that we are accessing a node only once leading to the,

Time complexity of Level Order Binary Tree Traversal using Recursion O(N).

where, N is the total number of nodes.

Auxiliary Space Complexity

The auxiliary space complexity have to consider two element. One is the call stack space due to recursion and other is due the 2D array that stores the level order values.

In the program, the left child recursive call will go on till we get the NULL value for the node, which is possible for the nodes with no left child. It will then go for the right child and same will continue till we encounter the node which does not have any children (i.e. leaf node). It infers that the number of stack required will be equal to the number of nodes for the given path from root node to the leaf node. And the max number of stack space will be required for the longest path which is the height of the tree.

So the worst case auxiliary space complexity for the recursive function is O(N). (for skew trees)

Now, for 2D array, it will always have the N number of elements at the end of execution. So, considering both requirements,

Auxiliary Space Complexity of Level Order Binary Tree Traversal using Recursion is O(N)

Applications of Level Order Binary Tree Traversal

Level order traversal is particularly useful in applications where processes need to be executed in a breadth-first manner. This includes scenarios such as:

• Real-time Decision Making: In AI and game development, decisions based on current state evaluations are critical.
• Serialization/Deserialization : Ensuring that data structures are serialized and deserialized in a breadth-first manner preserves structural integrity across operations.
• Building Index: Databases use binary trees for indexing where quick access to data is crucial.