Adjacency Matrix of a Directed Graph is a square matrix that represents the graph in a matrix form. In a directed graph, the edges have a direction associated with them, meaning the adjacency matrix will not necessarily be symmetric.

In a directed graph, the edges have a direction associated with them, meaning the adjacency matrix will not necessarily be symmetric. The adjacency matrix A of a directed graph is defined as follows:

What is Adjacency matrix of Directed graph?

For a graph with N vertices, the adjacency matrix A is an N X N matrix where:

• A[i][j] is 1 if there is a directed edge from vertex i to vertex j.
• A[i][j]​ is 0 otherwise.

Adjacency Matrix for Directed and Unweighted graph:

Consider an Directed and Unweighted graph G with 4 vertices and 4 edges. For the graph G, the adjacency matrix would look like:

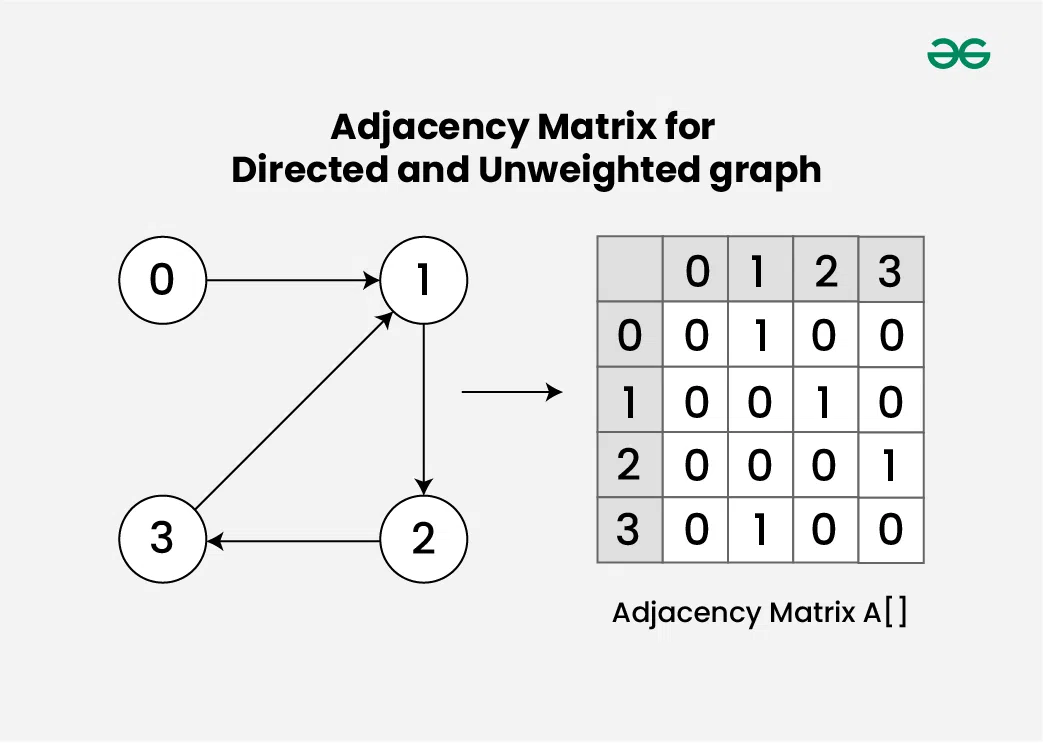
Here’s how to interpret the matrix:

• A[0][1] ​= 1, there is an edge between vertex 0 and vertex 1.
• A[1][2] ​= 1, there is an edge between vertex 1 and vertex 2.
• A[2][3] = 1, there is an edge between vertex 2 and vertex 3.
• A[3][1] = 1, there is an edge between vertex 3 and vertex 1.
• A[i][i] = 0, as there are no self loops on the graph.
• All other entries with a value of 0 indicate no edge between the corresponding vertices.

Adjacency Matrix for Directed and Weighted graph:

Consider an Directed and Weighted graph G with 5 vertices and 6 edges. For the graph G, the adjacency matrix would look like:

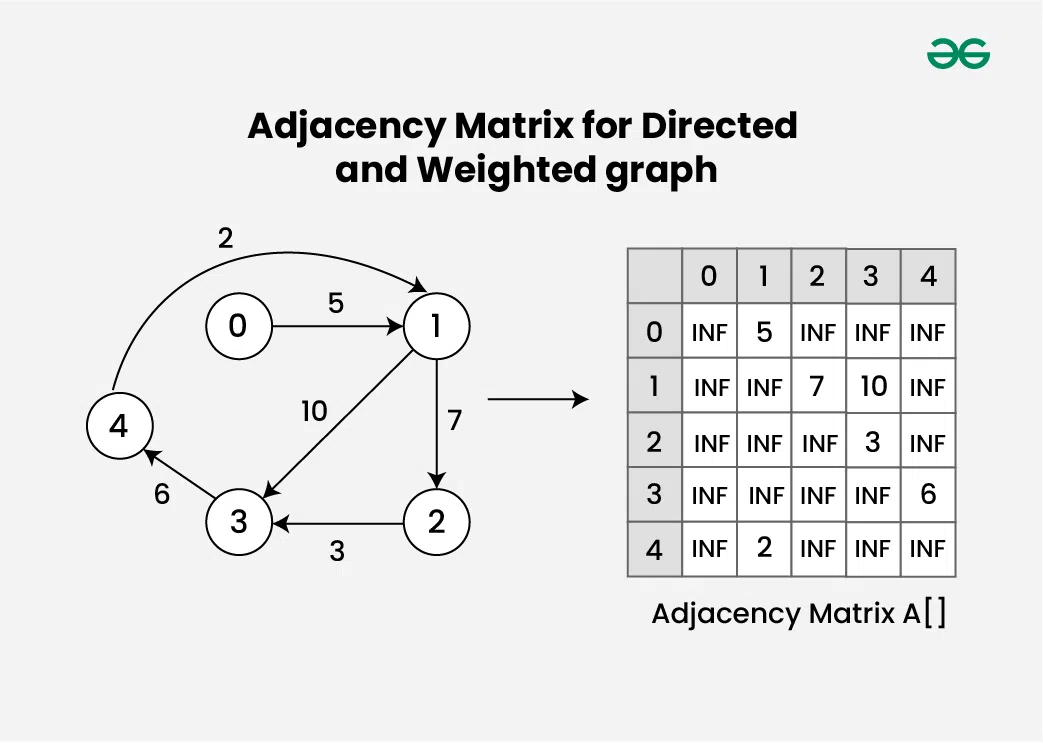
Here’s how to interpret the matrix:

• A[0][1] ​= 1, there is an edge between vertex 0 and vertex 1.
• A[1][2] ​= 1, there is an edge between vertex 1 and vertex 2.
• A[2][3] = 1, there is an edge between vertex 2 and vertex 3.
• A[3][1] = 1, there is an edge between vertex 3 and vertex 1.
• A[i][i] = 0, as there are no self loops on the graph.
• All other entries with a value of 0 indicate no edge between the corresponding vertices.

Properties of Adjacency Matrix of Directed Graph:

1. Diagonal Entries: The diagonal entries Aii​ are usually set to 0, assuming the graph has no self-loops.
2. Out-degree and In-degree: The number of 1’s in a row i (out-degree) indicates the number of outgoing edges from vertex i, while the number of 1’s in a column j (in-degree) indicates the number of incoming edges to vertex j.

Implementation of Adjacency Matrix of Directed Graph:

Below is the implementation of Adjacency Matrix of Directed Graph in different languages:

#include <algorithm>
#include <iostream>
#include <unordered_map>
#include <vector>

std::vector<std::vector<int> > create_adjacency_matrix(
    std::unordered_map<std::string,
                       std::vector<std::string> >
        graph)
{
    std::vector<std::string> vertices;

    // Get sorted list of vertices
    for (const auto& pair : graph) {
        vertices.push_back(pair.first);
    }
    std::sort(vertices.begin(), vertices.end());

    int num_vertices = vertices.size();

    // Initialize the adjacency matrix with zeros
    std::vector<std::vector<int> > adj_matrix(
        num_vertices, std::vector<int>(num_vertices, 0));

    // Fill the adjacency matrix based on the edges in the
    // graph
    for (int i = 0; i < num_vertices; ++i) {
        for (const auto& neighbor : graph[vertices[i]]) {
            int j = std::distance(
                vertices.begin(),
                std::find(vertices.begin(), vertices.end(),
                          neighbor));
            adj_matrix[i][j] = 1;
        }
    }

    return adj_matrix;
}

int main()
{
    // Example graph represented as a dictionary
    // The keys are the vertices and the values are lists of
    // neighboring vertices
    std::unordered_map<std::string,
                       std::vector<std::string> >
        graph = { { "1", { "2" } },
                  { "2", { "3" } },
                  { "3", { "4" } },
                  { "4", { "1" } } };

    // Create the adjacency matrix
    std::vector<std::vector<int> > adj_matrix
        = create_adjacency_matrix(graph);

    // Print the adjacency matrix
    for (const auto& row : adj_matrix) {
        for (int value : row) {
            std::cout << value << " ";
        }
        std::cout << std::endl;
    }

    return 0;
}

import java.util.ArrayList;
import java.util.Collections;
import java.util.HashMap;
import java.util.List;

public class AdjacencyMatrix {
    // Function to create an adjacency matrix from an
    // adjacency list
    public static int[][] createAdjacencyMatrix(
        HashMap<String, List<String> > graph)
    {
        // Get the list of vertices sorted in ascending
        // order
        List<String> vertices
            = new ArrayList<>(graph.keySet());
        Collections.sort(vertices);

        // Get the number of vertices in the graph
        int numVertices = vertices.size();

        // Initialize the adjacency matrix with zeros
        int[][] adjMatrix
            = new int[numVertices][numVertices];

        // Fill the adjacency matrix based on the edges in
        // the graph
        for (int i = 0; i < numVertices; i++) {
            // Get the neighbors of the current vertex
            List<String> neighbors
                = graph.get(vertices.get(i));
            for (String neighbor : neighbors) {
                // Find the index of the neighbor in the
                // sorted vertices list
                int j = vertices.indexOf(neighbor);
                // Set the corresponding entry in the
                // adjacency matrix to 1
                adjMatrix[i][j] = 1;
            }
        }

        return adjMatrix;
    }

    public static void main(String[] args)
    {
        // Example graph represented as an adjacency list
        // (unordered map)
        HashMap<String, List<String> > graph
            = new HashMap<>();
        graph.put("1", List.of("2"));
        graph.put("2", List.of("3"));
        graph.put("3", List.of("4"));
        graph.put("4", List.of("1"));

        // Create the adjacency matrix from the graph
        int[][] adjMatrix = createAdjacencyMatrix(graph);

        // Print the adjacency matrix
        for (int[] row : adjMatrix) {
            for (int value : row) {
                System.out.print(value + " ");
            }
            System.out.println();
        }
    }
}

// This code is contributed by shivamgupta0987654321

def create_adjacency_matrix(graph):
    """
    Create an adjacency matrix for a directed graph.

    Parameters:
    graph (dict): A dictionary representing the directed graph.

    Returns:
    list: The adjacency matrix of the graph.
    """
    vertices = sorted(graph.keys())  # Get sorted list of vertices
    num_vertices = len(vertices)

    # Initialize the adjacency matrix with zeros
    adj_matrix = [[0] * num_vertices for _ in range(num_vertices)]

    # Fill the adjacency matrix based on the edges in the graph
    for i, vertex in enumerate(vertices):
        for neighbor in graph[vertex]:
            j = vertices.index(neighbor)
            adj_matrix[i][j] = 1

    return adj_matrix


# Example graph represented as a dictionary
# The keys are the vertices and the values are lists of neighboring vertices
graph = {
    '1': ['2'],
    '2': ['3'],
    '3': ['4'],
    '4': ['1']
}

# Create the adjacency matrix
adj_matrix = create_adjacency_matrix(graph)

# Print the adjacency matrix
for row in adj_matrix:
    print(row)

function createAdjacencyMatrix(graph) {
    const vertices = Object.keys(graph).sort();
    const numVertices = vertices.length;

    // Initialize the adjacency matrix with zeros
    const adjMatrix = Array.from(Array(numVertices), () => Array(numVertices).fill(0));

    // Fill the adjacency matrix based on the edges in the graph
    for (let i = 0; i < numVertices; ++i) {
        for (const neighbor of graph[vertices[i]]) {
            const j = vertices.indexOf(neighbor);
            adjMatrix[i][j] = 1;
        }
    }

    return adjMatrix;
}

// Example graph represented as a dictionary
// The keys are the vertices and the values are lists of neighboring vertices
const graph = {
    "1": ["2"],
    "2": ["3"],
    "3": ["4"],
    "4": ["1"]
};

// Create the adjacency matrix
const adjMatrix = createAdjacencyMatrix(graph);

// Print the adjacency matrix
for (const row of adjMatrix) {
    console.log(row.join(' '));
}

[0, 1, 0, 0]
[0, 0, 1, 0]
[0, 0, 0, 1]
[1, 0, 0, 0]