When we make graphs, we usually use straight lines and grids to show data points. This is called a “linear coordinate system.” But sometimes, using a different system called “non-linear coordinates” can help us understand the data better.

What is a Non-Linear Coordinate system?

Non-linear coordinates can alter the appearance of geometric shapes, which differs from the behavior of linear coordinates. Non-linear coordinate systems can distort shapes. For example, in polar coordinates, a rectangle can turn into an arc. In map projections, the shortest path between two points might not be a straight line.

Non-Linear Coordinate system in ggplot2

Now, we’ll learn about non-linear coordinates and how they’re used in ggplot2, a tool in R Programming Language for making graphs. With examples and clear explanations, we’ll see how non-linear transformations in ggplot2 can make our graphs more insightful and easier to understand.

ggplot2 excels at plotting data using various coordinate systems. While the default is a rectangular plane with x and y axes, ggplot2 offers tools to explore your data in non-linear spaces. These transformations can significantly alter how data points are positioned and interpreted.

ggplot(data = NULL, mapping = aes())

Visualize data with inherent non-linearity: These systems allow you to represent relationships that aren’t well-suited for linear scales, such as exponential growth, logarithmic trends, or cyclical patterns.

• Reveal hidden insights: By transforming data using non-linear scales, you can uncover patterns that might be obscured in a linear plot.
• Create specialized visualizations: Certain coordinate systems (e.g., polar coordinates) are designed for specific data types, enabling you to create tailored plots.
• Changing Parameterization to Location-Based Representation: First, we change how we describe each shape. Instead of using both its location and size, we only focus on its location. For example, a bar can be described by its position on the x-axis (location), its height, and its width (dimensions).

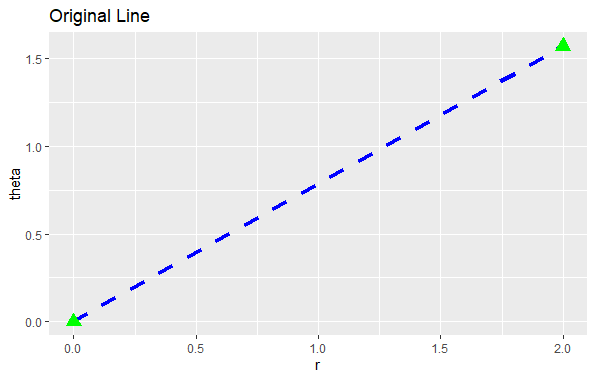
Once all shapes are described by their location, we move on to the next step: changing their location to fit the new coordinate system. It’s simple to move points because they stay the same no matter the coordinate system. However, lines and polygons are tougher because a straight line might not be straight anymore in the new system. To handle this, we assume that all changes in coordinates are smooth, meaning very short lines in the old system will still be very short and straight in the new one. With this assumption, we can transform lines and polygons by breaking them into small segments and transforming each segment separately. This process is called “munching.”

Step 1: Define the original line with its two endpoints

library(ggplot2)
#Starting with a line defined by its two endpoints
df <- data.frame(r = c(0, 2), theta = c(0, pi/2))  

# Visualizing the original line with different design
ggplot(df, aes(r, theta)) + 
  geom_line(color = "blue", size = 1.5, linetype = "dashed") + 
  geom_point(size = 4, colour = "green", shape = 17) +  
  labs(title = "Original Line")  

Output:

Non-Linear Coordinate system in ggplot2

Step 2: Divide the line into smaller segments

# Dividi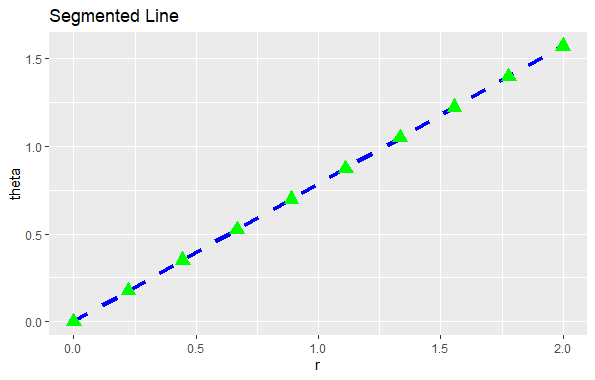ng the line into smaller segments
interp <- function(rng, n) {
  seq(rng[1], rng[2], length = n)
}
munched <- data.frame(
  r = interp(df$r, 10),  
  theta = interp(df$theta, 10)  
)

# Visualizing the segmented line with different design
ggplot(munched, aes(r, theta)) + 
  geom_line(color = "blue", size = 1.5, linetype = "dashed") +  
  geom_point(size = 4, colour = "green", shape = 17) +  
  labs(title = "Segmented Line")  

Output:

Non-Linear Coordinate system in ggplot2

In this step, we generated 19 points between the endpoints of the original line to create smaller line segments.

Step 3: Adjust the position of each segment to fit into the new coordinate system

#Adjust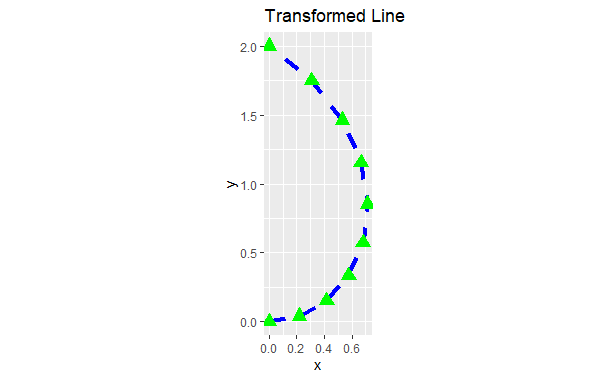ing the position of each segment
transformed <- transform(munched,
  x = r * cos(theta),  
  y = r * sin(theta)   
)

# Visualizing the transformed line with different design
ggplot(transformed, aes(x, y)) + 
  geom_path(color = "blue", size = 1.5, linetype = "dashed") +  
  geom_point(size = 4, colour = "green", shape = 17) +  
  coord_fixed() +  
  labs(title = "Transformed Line")  

Output:

Non-Linear Coordinate system in ggplot2

Transformation using coord_polar()

coord_polar() is an example of a non-linear transformation in ggplot2. It transforms the rectangular coordinate system into a circular one, where:

• The x-axis becomes the angle (theta), typically measured in radians (0 to 2π).
• The y-axis becomes the radius, representing the distance from the origin.

This transformation is particularly useful for creating

• Pie Charts: By assigning categories to the angle (theta) and their values to the radius, you can visualize the proportional contribution of each category.
• Radar Charts: In this, multiple variables radiate from a central point, with each variable occupying a specific angle and its value represented by the distance from the center.
• Other Circular Plots: coord_polar() opens doors for creative visualizations like wind rose plots or flow charts with a circular layout.

For example, let’s say we have data representing the time spent on various activities during a day. We can use polar coordinates to plot this data on a circular graph. In this case, each activity would be represented by a segment of the circle, and the length of the segment would show the amount of time spent on that activity.

• However, there’s a downside to using polar coordinates. It’s not easy to accurately perceive angles for small segments of the circle compared to larger segments. So, while polar coordinates are great for circular data, they may not always provide the best visual perception.
• In plotting with polar coordinates, we use the “theta” argument to decide which variable represents the angle (by default, it’s the x-axis), and which represents the radius (the distance from the center of the circle).
• Imagine transforming a scatter plot. Instead of positioning points based on their x and y values, coord_polar() calculates an angle (theta) based on the x-value and a radius based on the y-value. These values then determine the point’s location within the circular coordinate system.

Let’s create a pie chart using coord_polar() to visualize the distribution of categorical data. This code will produce a pie chart where each fruit slice corresponds to a category in the “fruits” column, and its size represents the corresponding count in the “counts” column.

librar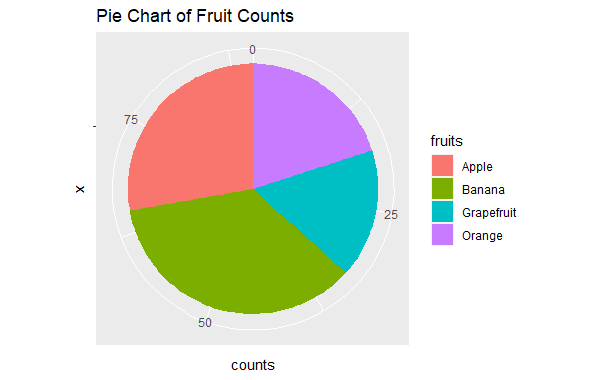y(ggplot2)

# Sample data for fruit categories and their counts
fruits <- c("Apple", "Orange", "Banana", "Grapefruit")
counts <- c(25, 18, 32, 15)

# Create a DataFrame
data <- data.frame(fruits, counts)

# Pie chart using coord_polar()
ggplot(data, aes(x = "", y = counts, fill = fruits)) +
  geom_col(width = 1) +  # Adjust width for better separation
  coord_polar("y") +     # Theta mapped to "y" (radius)
  labs(title = "Pie Chart of Fruit Counts")

Output:

Non-Linear Coordinate system in ggplot2

Transformation using coord_trans()

coord_trans() allows you to define custom functions that transform data points from the default rectangular system into a non-linear one. This function takes arguments for the x and y axes, where each argument can be:

• A string representing a built-in transformation (limited options)
• A function you define to create your own transformation

This flexibility lets you tailor the visualization to your specific needs and data characteristics.

Just like how you can set limits on a graph, you can also change how the data is shown in two ways: either by changing the scale or by changing the coordinate system. When you change the scale, it happens before any calculations are done on the data and doesn’t transform the shape of what you’re plotting. But when you change the coordinate system, it happens after the calculations are done and it can change the shape of what’s plotted. By using both methods together, you can adjust how the data looks for analysis, and then change it back to its original form for interpretation.

librar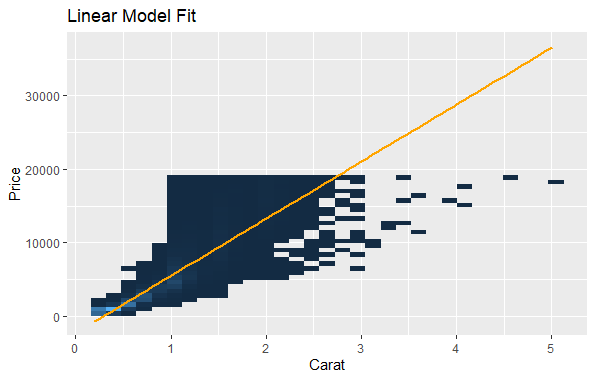y(ggplot2)

# Linear model on original scale is a poor fit
base <- ggplot(diamonds, aes(carat, price)) + 
  stat_bin2d() + 
  geom_smooth(method = "lm", color = "orange") +  
  xlab("Carat") +   # Adding x-axis label
  ylab("Price") +   # Adding y-axis label
  theme(legend.position = "none") +
  ggtitle("Linear Model Fit")  # Adding plot title

print(base)  

Output:

Non-Linear Coordinate system in ggplot2

In this plot, we’re fitting a linear model to the data without any transformation. Then, we will apply transformation to it.

Now, we will transform both the x-axis and y-axis to logarithmic scales.

# Better 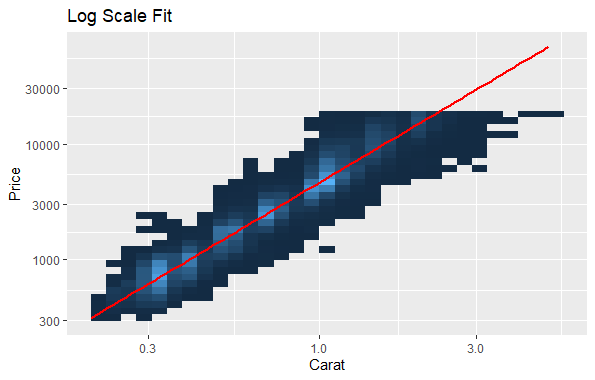fit on log scale, but harder to interpret
log_scale_plot <- base +
  scale_x_log10() +  
  scale_y_log10() +  
  geom_smooth(method = "lm", color = "red") +  
  ggtitle("Log Scale Fit")  

print(log_scale_plot)

Output:

Non-Linear Coordinate system in ggplot2

We will apply a logarithmic transformation to both the x-axis and y-axis using scale_x_log10() and scale_y_log10(). This transformation will make it easier to visualize the data when there’s a wide range of values. We will fit a linear regression line with geom_smooth(method = “lm”).

Transformation using coord_map()

The Earth is a sphere, but most maps portray it as flat. This transformation, called a map projection, inevitably distorts shapes, distances, and areas depending on the chosen projection. coord_map() leverages the mapproj package to incorporate various map projections into your ggplot2 visualizations.

coord_map() transforms your data points from geographic coordinates (latitude and longitude) onto a projected flat map. It offers:

• Variety of Projections: Choose from a wide range of projections available in mapproj, each suited for representing specific regions or emphasizing particular aspects (e.g., equal area, conformal, etc.).
• Control Over Projection Parameters: Fine-tune the projection behavior by passing arguments understood by mapproj::mapproject(). This allows you to customize the central point, orientation, and other aspects.

When we look at maps, we often see a flat representation of a round Earth. But plotting raw latitude and longitude directly can be misleading because the Earth’s surface is curved. So, we need to project the data onto a flat surface. There are two main ways to do this in ggplot2:

• coord_quickmap(): This is a quick and simple way to approximate map projections. It adjusts the aspect ratio of the map so that 1 meter of latitude and 1 meter of longitude are the same distance in the middle of the plot. It’s good for smaller regions and is very fast.
• coord_map(): This method uses the mapproj package to do a formal map projection. It offers more control over the projection and can handle more complex cases. However, it’s slower than coord_quickmap() because it needs to process and transform each piece of data.

Let’s first load world map data using map_data(“world”). ggplot() creates a basic plot of the world map using longitude and latitude coordinates. geom_path() draws the outlines of the countries on the map. scale_y_continuous() and scale_x_continuous() customize the y-axis and x-axis respectively, setting breaks and labels to control the appearance of the map. Then, we will do Map Projection with coord_map(), coord_map() is used to perform a formal map projection. This projection is suitable for general-purpose maps.

# Load wo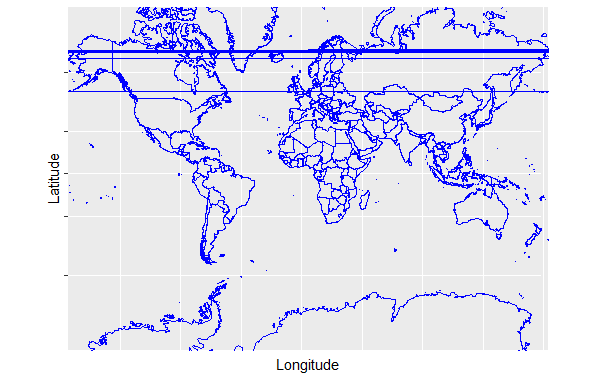rld map data
usedworld <- map_data("world")

# Create a customized world map plot
custom_worldmap <- ggplot(usedworld, aes(long, lat, group = group)) +
  geom_path(color = "blue") +  # Changing the color of the map outlines
  scale_y_continuous(name = "Latitude", breaks = (-2:3) * 30, labels = NULL) +  
  scale_x_continuous(name = "Longitude", breaks = (-4:4) * 45, labels = NULL)   

# Plot the basic map
custom_worldmap + coord_map()

Output:

Non-Linear Coordinate system in ggplot2

We can also use the “ortho” argument in coord_map() to specify an orthographic projection. An orthographic projection displays the Earth as if viewed from a great distance, resulting in a globe-like appearance. This projection is suitable for visualizing the entire Earth from a global perspective.

custom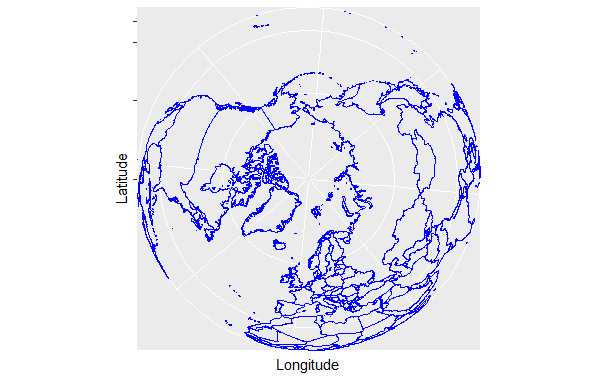_worldmap + coord_map("ortho")

Output:

Non-Linear Coordinate system in ggplot2

Applications

1. Visualizing Stock Market Returns: Use a logarithmic y-axis to better understand long-term trends in stock prices.
2. Analyzing Weather Patterns: Create a wind rose plot using polar coordinates to visualize wind direction and speed across different seasons.
3. Mapping Global Population Density: Use an equal-area projection to display population distribution without being skewed by the size of continents on a rectangular map.
4. Creating a Custom Spiral Plot: Define a custom function to generate a spiral pattern of points, which can be aesthetically pleasing or used to represent specific data relationships.