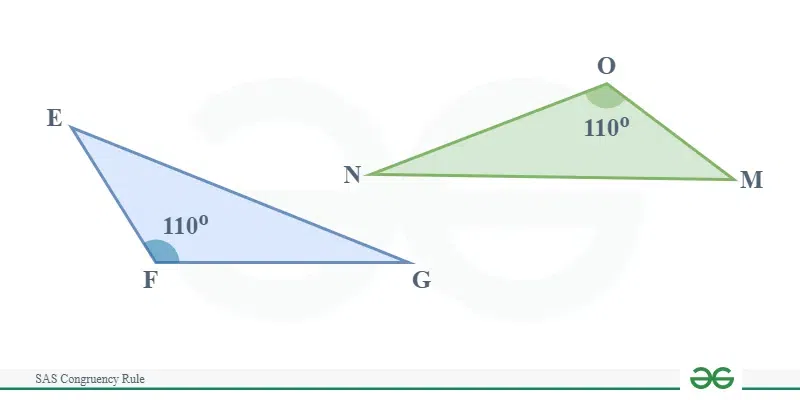
SAS Congruence Rule: SAS Congruence Rule is a principle in geometry that provides a method for determining if two triangles are congruent, meaning they have the same size and shape. SAS stands for Side-Angle-Side, indicating that if two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the two triangles are congruent.

Condition of Congruency of Two Triangle: When the two sides of a triangle are equal to the two sides of another triangle, and the angles formed by these sides (the included angles) are also equal, then the two triangles are congruent Congruence between any two geometric objects is represented by “≅” which reads as ‘is congruent to’.

In this article, we will discuss the SAS Congruence Rule and criteria of congruence of right-angle triangles with examples and proof.

What is Congruence?

Congruence is a term used in mathematics to describe a relationship between geometric figures or mathematical objects that have the same shape and size. In other words, if one figure can be transformed into the other by a combination of translations, rotations, and reflections without changing its shape or size, then they are considered congruent.

For example, two triangles are congruent if their corresponding sides are equal in length and their corresponding angles are equal in measure. Congruence is often denoted by the symbol “≅”.

Read More: Congruence of Triangles

What is SAS Congruence Rule?

SAS stands for Side-Angle-Side.

The SAS Congruence Rule means that when the two sides of a triangle are equal to the two sides of another triangle, and the angles formed by these sides (the included angles) are also equal, then the two triangles are congruent.

The SAS congruence rule is one of the ways to verify two or more triangles are exactly the same. By ‘same’ we mean that the triangles have all three corresponding sides equal to that of one another and that all the corresponding angles are equal too.

SAS Congruence Rule Definition

The Side-Angle-Side (SAS) Congruence Rule is a principle in geometry that states if two sides and the included angle of one triangle are exactly equal to two sides and the included angle of another triangle, then the two triangles are congruent.

Criteria for SAS Congruence Rule

For ΔABC and ΔDEF, if

• AB = DE
• AC = DF
• ∠BAC = ∠EDF

Then, by SAS Congruence Rule,

• ΔABC ≅ ΔDEF

By CPCT property [Corresponding Parts of Congruent Triangles are equal], we can further imply the following as well:

• ∠B = ∠E
• ∠C = ∠F
• BC = EF

SAS Congruence Rule Proof

Theorem: If you have two triangles where two sides of one triangle are the same lengths as two sides of another triangle, and the angles between those sides are also the same, then those triangles are exactly the same shape and size (congruent).

To prove the side angle side theorem (SAS), we will need:

(1) The Axiom of Movement 

(2) The Mid-Point Theorem

1. Axiom of Movement: This means we can move any shape around without making it bigger or smaller. So, if you have a triangle, you can slide it or turn it without changing its size or shape.

2. Mid-Point Theorem: If you have a triangle, and you draw a line connecting the middle points of two of its sides, that line will be parallel to the third side of the triangle. Plus, it will be exactly half as long as that third side.

Proof:

Given. ABC, DEF are triangles such that. 

AB = DE 

AC = DF 

< BAC = < EDF 

To prove. ∆s ABC, DEF are congruent 

SAS Congruence Theorem Proof

Construction:

1. Move Triangle DEF onto Triangle ABC: Use the axiom that allows us to move shapes without changing their size or shape. Place point D on point A and point E on point B, and make sure that the line segment DE lines up with line segment AB.
2. Rotate Triangle DEF: Rotate triangle DEF 180 degrees around point A. Imagine spinning triangle DEF in a way that it flips over but stays attached at point A.
3. Create a Cross Section: After the rotation, you’ll have a shape that looks like a double cone. Draw a line connecting point E and point C, and from the point where A and D overlap on this shape, draw a line called HK. This line HK should cut the line EC in half at a point we’ll call K.
4. Define H: We use the notation H = (A;D) to mean that H can refer to either point A or point D, depending on which triangle we’re talking about, ABC or DEF.

Prove the Theorem:

To prove the theorem, we need to show that the length of line segment BC is equal to the length of line segment EF. This will confirm that the triangles are congruent by SSS Congruence.

Proof: 

< BHC = < EHF (given) 

But these are vertically opposite angles  

Therefore, Lines BE, CF are straight line.

In ∆BCE, 

BH = EH (given) 

CK = EK (construction)  

Therefore, HK bisects BE and EC.  

We can say, HK = ½ BC (Mid-Point Theorem)

Similarly in ∆EFC, 

HK bisects CF and CE (Construction)  

We can say, HK = ½ EF (Mid-Point Theorem)

BC = EF (If P=Q, Q=R then P=R)  

∆s ABC, DEF are congruent.

How to apply SAS Congruence Rule?

To apply SAS congruence rule, we can use the following steps:

To check if you can apply the SAS Congruence Rule to prove whether triangles are congruent, check the given and the triangles.

If it is given or if you can measure or verify any two sides of a triangle to be equal to the corresponding two sides of another triangle and check if the angle between those 2 sides are equal for both triangles, then you can apply the SAS Congruence Rule to prove them to be congruent to each other.

If all the three conditions above meet then you can apply the SAS Congruence Rule to prove them to be congruent to each other.

SAS Similarity Criteria

According to SAS similarity criterion,

if ∠A = ∠X and AB/XY = AC/XZ then ΔABC ~ ΔXYZ.

This criterion is referred to as the SAS (Side–Angle–Side) similarity for two triangles.

Using this similarity criteria, we can imply further

• AB/XY = BC/YZ = AC/XZ
• ∠B = ∠Y
• ∠C = ∠Z

Note: Symbol ‘⁓’ stands for ‘is similar to’ and is used to state the similarity between two triangles or any other geometric shape.

Theorem (SAS Similarity Criterion)

If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar.

Read More: Similar Triangles

Congruence vs Similarity | Difference Between Congruence and Similarity

The key differences between congruence and similarity are: