Damped Oscillation means the oscillating system experiences a damping force, causing its energy to decrease gradually. The level of damping affects the frequency and period of the oscillations, with very large damping causing the system to slowly move toward equilibrium without oscillating.

In this article, we will look into damped oscillation, damped oscillator, damping force, general equation derivation, application and type of damped oscillation, etc.

What is Damped Oscillation?

Damped oscillation refers to the condition in which the amplitude of an oscillating system gradually decreases over time due to the dissipation of energy by non-conservative forces, such as friction or air resistance. This phenomenon is observed in various systems, such as mass oscillating on a spring or shock absorbers in a car. Damped oscillations are classified as underdamped, critically damped, and overdamped based on the damping constant. The damping force causes the amplitude of the oscillations to decrease gradually, leading to a loss of energy from the system.

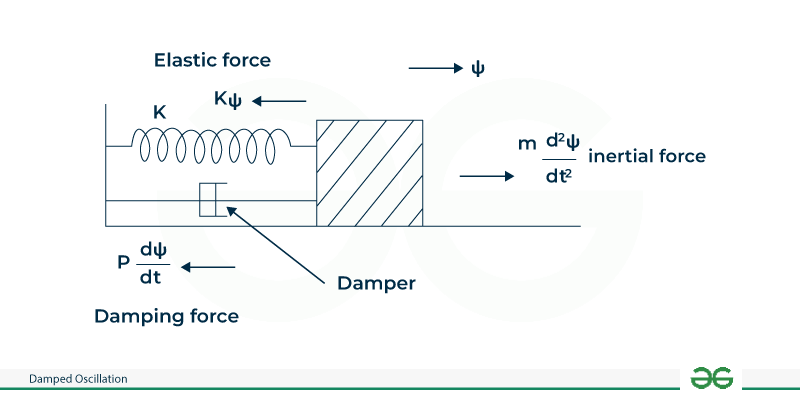
Definition of Damped Oscillation

Damped oscillation refers to an oscillatory motion in which the amplitude of the oscillation gradually decreases over time. This decrease in amplitude is due to the dissipation of energy from the system, often due to friction or other resistive forces.

Damped Oscillator

A simple harmonic oscillator whose amplitude of vibrations always reduces with time and, finally, the system comes to rest due to the unavoidable presence of damping force is called a Damped oscillator.

Damping Force

Damping force is the external force present in the surroundings, which acts against the oscillatory motion of the system. The magnitude of the damping force determines the way in which the motion proceeds. The damping force is always directly proportional to the velocity of the oscillatory system.

Damped Oscillation Differential Equation

The equation of motion for a damped harmonic oscillation is a second-order ordinary differential equation. It can be expressed as:

md²x/dt² + 2μ.dx/dt + ω₀²x(t) =0

Where:

• m is the mass of the object,
• x(t) is the position of the object as a function of time,
• 2μ is the damping coefficient,
• ω₀ is the natural frequency of the oscillator

Damped Harmonic Oscillator

Consider a body of mass’ m’ is set to the oscillatory motion in air with velocity v.

Let ‘k” be the restoring force constant of the system.

For ideal SHM (neglecting any opposition/ damping), the differential equation of motion is written using Newton’s 2nd law

m.a = F_total

m.d²x/dt² = -kx……(1)

In real situation, there is always some resistance offered to moving body such that. The damping force is directly proportional to the velocity of the oscillatory body.

Damping force = -bv ……………..(2)

Where b = damping constant

Considering damping force in the equation 1, we get

m.d²x/dt² = -kx – bv…..(3)

Using equation 3 and rearranging, we get

Dividing both sides with ‘m’ and rearranging, we get

d²x/dt² = -kx/m – bv/m

d²x/dt² = -(k/m)x – (b/m)v

d²x/dt² = -(k/m)x – (b/m)dx/dt

d²x/dt² +(k/m)x +(b/m)dx/dt=0……(4)

Let √(k/m) = ω₀

And b/m = 2μ

d²x/dt² + ω₀²x + 2μ.dx/dt=0….(5)

ω₀: natural frequency (angular) of the system.

μ: damping factor (damping force per unit mass at any instant when vibrating body moving with unit velocity)

Equation 5 is called the differential equation of motion for a damped oscillatory system, which describes the motion of any damped oscillatory motion.

Using differential operator D = d/dt, equation 5 is reduced to the following.

D²x + ω₀x + 2μxD = 0

(D²+ ω₀ + 2μD)x = 0…..(6)

Here, x represents displacement at any instant of time; hence

x ≠ 0

(D²+ ω₀²+2μD) = 0……(7)

Solving equation 7 as a quadratic equation, we get

D= {-2μ±√[(2μ)²- 4ω₀²]}/2

D= -μ±√μ²- ω₀²…..(8)

As shown in equation 8, D has two possible values of the square root

α = -μ+√μ²-ω₀² and β = -μ-√μ²-ω₀²

D = d/dt

Dx = dx/dt

⇒ dx/dt = αx….(8a) and dx/dt = βx….(8b)

Consider equation 8a; rearranging and integrating, we get

∫dx/dt = αx and ∫dx/dt = βx

∫dx/x = ∫ αdt = Ae^αt….(9a)

∫dx/x = ∫βdt = Be^βt….(9b)

Equation 9a and 9b are both possible solutions of the differential equation (equation 5); hence, the general solution is given as

x(t) = Ae^αt +Be^βt

x(t)={Ae^{[-μ+√µ²-ω0²]}t + Be^{[-μ-√µ²-ω0²]t}]

x(t)=e^-μt{Ae^{[√µ²-ω0²]t} + Be^{[-√µ²-ω0²]t}]…(10)

Equation 10 is the general solution of the differential equation of motion (equation 5) for the damped oscillator.

It helps us to determine the displacement’ x’ of the oscillatory system at any instant in time. In this equation, A and B are the constants that depend on the oscillatory system. The term e^-μt represents the exponential decay of the displacement (amplitude) with respect to time.

Damped Oscillation Equation

The general equation of differential equation can be represented as follows:

x(t) = e^-μt{Ae^{[√µ²-ω0²]t}+ Be^{[-√µ²-ω0²]t}]

Damped Oscillation Formula

The equation gives the formula for the damped oscillation of a harmonic oscillator:

x(t) = x₀​e ^{– μω0​t} cos(ω_d​t+ϕ)

Where,

• x(t) is the displacement at time
• x₀​ is the initial displacement,
• μ is the damping ratio,
• ω₀ is the undamped angular frequency,
• ω_d​ is the damped angular frequency, and
• ϕ is the phase angle.

Damped Harmonic Oscillator Cases

In a damped harmonic oscillator, three cases are distinguished based on the damping level:

• Large Damping: In systems with very large damping, oscillations do not occur; instead, the system slowly moves towards equilibrium. The displacement of the oscillator moves more slowly towards equilibrium than critically damped systems.
• Critical Damping: Critical damping occurs when the damping constant equals the square root of 4 times the mass multiplied by the spring constant. Systems under critical damping return to equilibrium as quickly as possible, like shock absorbers in cars, without overshooting.
• Small Damping: In underdamped systems, oscillations occur while the amplitude decreases exponentially until the system comes to rest. These systems oscillate through the equilibrium position and eventually approach zero amplitude.

Damped Oscillations Having One Degree of Freedom

A damped oscillation of a system with one degree of freedom refers to the behavior of a simple system with one moving part subject to a linear viscous damping force. The system is assumed to have a small velocity, and the damping force is proportional to the velocity. The system’s motion can be described by a differential equation known as the damped harmonic oscillator equation, which can be solved to find the displacement and velocity of the system as a function of time.

d²x/dt² = -(k/m)x – (b/m)dx/dt

This equation is for small displacements and velocities. The equation can be rewritten to:

md²x/dt² +ω₀²x(t) +2μ.dx/dt=0

The system’s behavior depends on the character of the roots of the equation, which may be real or complex. The damping present in the system can be characterized by the quantity gamma, which has the dimension of frequency, and the constant ω₀ represents the natural angular frequency of the system in the absence of damping. The system’s behavior can be heavily, weakly, or critically damped, depending on gamma values and ω₀.

Types of Damped Oscillator

Damped oscillators are classified into three main types based on the damping ratio: overdamped, critically damped, and underdamped.

Overdamped Oscillator

In this type, the system returns to equilibrium without oscillating. The motion decays more slowly toward equilibrium than in a critically damped system.

The oscillatory system, where the damping force experienced by the system from the surroundings is larger than the restoring force of the system such that (µ > ω₀) is called Overdamped oscillation.

The equation of displacement for overdamped oscillation is

x(t) = e^-μt{Ae^{[√µ²-ω0²]t} + Be^{-[√µ²-ω0²]t}]

Overdamped motion is non-oscillatory. In this case, the amplitude decreases exponentially, reaching equilibrium very slowly. (In an ideal case, it takes infinite time to reach equilibrium.)

Critically Damped Oscillator

Here, the system returns to equilibrium as quickly as possible without oscillating. Shock absorbers often exemplify this type in cars, where oscillations decay rapidly. The oscillatory system, where the damping force experienced by the system from the surroundings is well balanced by the restoring force of the system such that (µ² = ω₀) is called a critically damped oscillation.

The time rate equation of displacement for critically damped oscillation is

X(t)= e^-μt ( A + Bt)

Critically damped motion is non-oscillatory. In this case, the amplitude decreases exponentially, reaching equilibrium much faster than over-damped conditions.

Underdamped Oscillator

This type oscillates at a frequency slightly different than the undamped case and gradually returns to equilibrium. An example is a weight on a spring with some damping, where the motion slowly comes to rest. The oscillatory system, where the damping force experienced by the system from surrounding is less than the restoring force of the system such that (µ << ω0) is called an underdamped damped oscillation.

The time rate equation of displacement for underdamped oscillation is

x(t) = (e^-μt).sin(qt+θ)

Where q = √(ω₀²-μ²)

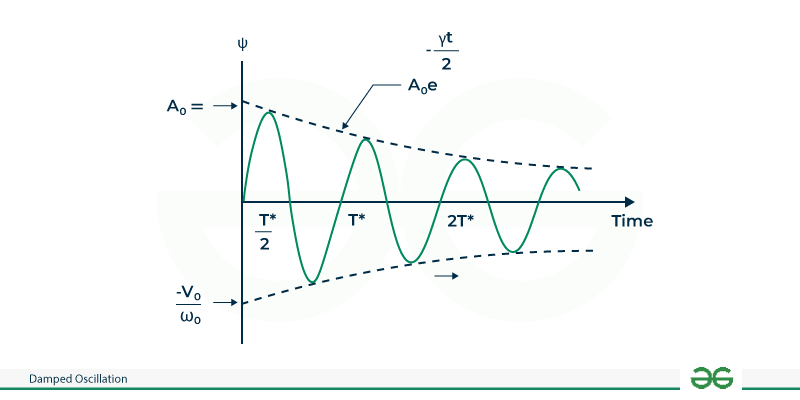
Underdamped damped motion is an oscillatory motion whose amplitude declines with time and reaches equilibrium. The decay of amplitude with each oscillation is governed by e^-μt.

These classifications are based on the system’s behavior due to the presence of damping forces, and they have implications in various fields such as mechanics, electronics, and physics.

Effects of Damping

The effect of damping on oscillations can be summarized as follows:

Reduction of Amplitude

Damping causes the oscillation amplitude to diminish gradually over time. The amplitude decreases exponentially with time, leading to a reduction in the extent of the oscillations.

Change in Frequency

The angular frequency of the damped oscillation is different from the frequency of the undamped oscillation. The damped frequency is lower, leading to a change in the oscillatory behavior.

Damping Ratio

The damping ratio measures how oscillations in a system decay after a disturbance. It influences the behavior of the oscillatory system, leading to different types of damping such as underdamped, critically damped, and overdamped, each with its own characteristic oscillatory behavior and speed.

In short, damping in oscillatory systems leads to a gradual decrease in the amplitude of oscillations and a change in the oscillatory behavior, which is characterized by the damping ratio.

Relaxation time

The time required to reduce the amplitude to(1/e) of its original value is called relaxation time. It is given as:

τ = 1/μ

Proof of Relaxation Time

We know that

a(t)= a₀e^-μt

Therefore t = τ = a(τ) = a₀/e^μt = a₀e^-μt as 1/e = e^-μt

Hence, τ = 1/μ = 2m/b as (μ=b/2m)

Where,

• T is a relaxation time
• μ is a damping coefficient
• m is a mass, and b is a damping constant

Logarithmic decrements

Natural Logarithmic ratio of the two consecutive peaks of any underdamped system. It is the measure of the rate at which the amplitude of the underdamped system is declining.

Let a_n and a_n+1 be two successive maximums corresponding to displacement a_n and a_n+1 and separated by time period

T = (2π/α) Such that, a_n= a₀e^-μt and a_n+1= a₀e^-μ(t+T)

Let a_n/a_n+1 = a₀e^-μt/a₀e^-μ(t+T) = 1/e^-μT = e^μT

Therefore ln(a_n/a_n+1)= μT =∆ (Log decrement)

Damped Oscillation Example

Examples of damped oscillation include:

• Mass on a Spring: When a mass is attached to a spring and immersed in a fluid, the system undergoes damped oscillation. The amplitude of the oscillation decreases over time due to the damping force exerted by the fluid.
• Pendulum in a Viscous Medium: A pendulum swinging in a medium with significant viscosity experiences damped oscillation. The damping force from the medium causes the pendulum’s amplitude to decrease over time, eventually leading to the pendulum coming to rest.
• RLC Circuit: In an electrical circuit consisting of a resistor, inductor, and capacitor (RLC circuit), damped oscillations occur due to the energy dissipation in the resistor. The oscillations in the circuit decrease over time due to the damping effect of the resistor.
• Shock Absorbers in a Car: The motion of a car’s shock absorbers represents damped oscillation. The shock absorbers dampen the oscillatory motion of the car’s suspension system, causing the vehicle to return to a steady state without oscillating, thus demonstrating critically damped behavior.

Energy of Weaker damped oscillator system

The reduction of the amplitude of the damped oscillator system indicated a continuous decrease in the system’s energy.

The total energy of the system any time ‘t’ is given as

E(t)= K.E + P.E

E(t)=½mv²+ ½kx²

E(t)=½m(dx/dt)²+ ½kx²

Let us consider an underdamped system. Therefore, the displacement of an oscillatory system w.r.t time is given as

X(t)=e^{-μtsin(qt+θ)}

Therefore, dx/dt =d/dt {e^{-μtsin(qt+θ)}}

dx/dt=a₀(e^{-μtqcos(qt+θ)}– μe^{-μtsin(qt+θ)})

dx/dt=a₀e^{-μtq(cos(qt+θ)} – μ/qsin(qt+θ))….(3)

For underdamping oscillations

(µ<<ω₀) and q=√ω₀²- μ² = μ<<q = μ/q<<1 = μ/qsin(qt+θ)<<<1

Therefore, equation (3) become

dx/dt=a₀e^{-μtq(cos(qt+θ)}….(4)

Using (1).(2)and(4) we have

K.E=½m(dx/dt)²= ½m[a₀e^{-μt.q(cos(qt+θ)}]²…..(5)

P.E = ½kx²= ½k[a₀e^{-μt.sin(qt+θ)}]²……(6)

Substituting equations (5)and (6) in (1), we get,

E(t) = ½m[a₀e^{-μtq(cos(qt+θ)}]² + ½k[a₀e^{-μtsin(qt+θ)}]²

E(t) = ½a₀²e^-2μt(mq²cos²(qt+θ)+k.sin²(qt+θ))

E(t) = ½a₀²(e^-2μt)m(q²cos²(qt+θ)+k/m.sin²(qt+θ))….(7)

We know that q=√ω₀²-μ²=q²=ω₀²-μ²

If ω₀²>>μ²=q²≈ω₀²=k/m

Using this value in equation (7), we get

E(t) = ½a₀²(e^-2μt).m(k/m.cos²(qt+θ)+k/m.sin²(qt+θ)).

E(t) = ½a₀²(e^-2μt).k(cos²(qt+θ)+sin²(qt+θ)).

E(t) = ½a₀²(e^-2μt).k. (at t=0,E(0)=½a₀²k=E₀)

E(t) = E₀(e^-2μt)………(9)

Equation 9 represents the energy of the damping oscillator system at any time t.

As the system continuously works against the damping force, the energy of the damped oscillator system also decreases with time.

Application of damping oscillation

The damped oscillation has various practical applications in different fields. Some of the common applications include:

• Shock Absorbers for Vehicles: Shock absorbers in vehicles are designed to dampen the oscillations of the vehicle, allowing it to return to its equilibrium position quickly and smoothly.
• Pendulum Clocks: Damping is essential in pendulum clocks to control the pendulum’s oscillations and ensure accurate timekeeping.
• Musical Instruments: Damping is used in musical instruments to control the resonance and sustain of the sound produced.
• Engineering and Construction: Damped oscillation is utilized in engineering and construction to reduce the effects of vibrations and prevent damage to structures or equipment.