All of the topics covered in the Control System Tutorial, including the Introduction to Control Systems, Classification, Transfer Function, Signal Flow Graphs, Mason Gain Formula, Block Diagram, State Space Model, and more, are included in our tutorial.

The compensator is an extra part that is introduced to the control system’s structure throughout its redesign. It is included in order to make up for the system’s poor performance. A compensator can be mechanical, electrical, hydraulic, or any combination of these.

What is a Compensator?

The word compensation is the root of the compensators. It refers to rearranging a structure’s components to achieve optimal performance. The control system’s feedback mechanism must function properly. Adjustment can occasionally play a significant role in achieving acceptable feedback performance and system improvement. The reason for this is because we frequently need to adjust or modify the system’s parameters.

In these situations, a compensator aids in enhancing the functionality of the control system. Basic and advanced Control System Library ideas are covered in the Control Systems Tutorial. Our Control System Tutorial is appropriate for both novices and experts.

Types of Compensator

• Lead compensator
• Lag compensator
• Lag-lead compensator

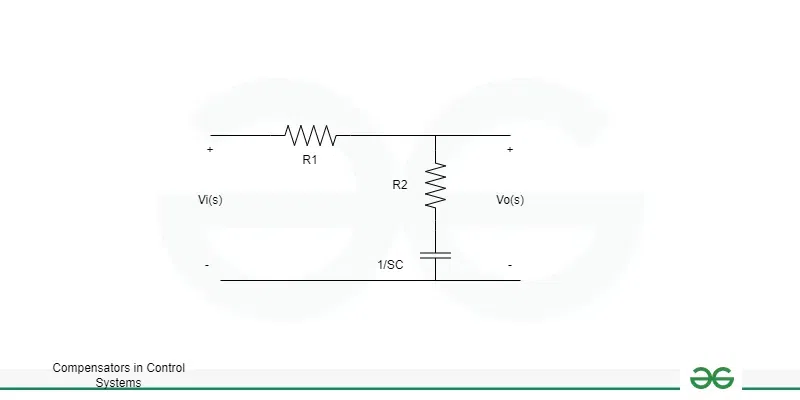
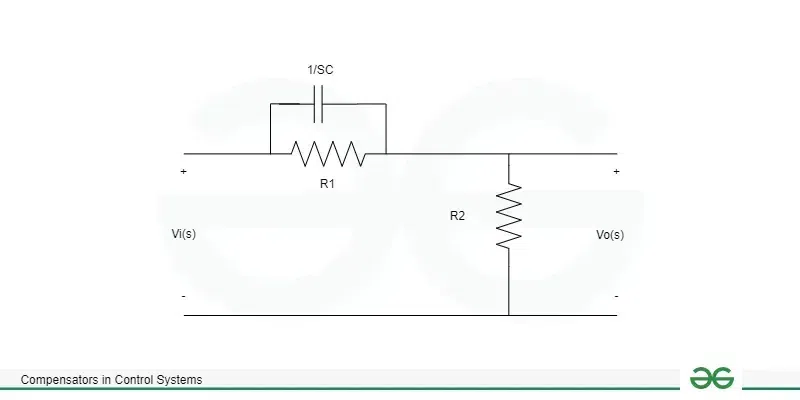
Lead Compensator

In a control system, the phase lead is used to produce the output by the lead compensator. Lead in this context refers to ahead. This kind of action is a successor to it.

It is made up of one capacitor C and two resistors, designated R₁ and R₂.

Lead Compensator circuit

The transfer function is defined as the H(s) which is ratio of output voltage to input voltage.

H(s) = V_o(s) / V_i(s)

Here , V_o(s) = R₂

The elements in series or parallel configuration (capacitor and resistors) will be the input. The capacitor C1 and resistor R1 are linked in parallel. The resistor R2 is further linked in series with the equivalent parallel combination.

=> R₁(1/Cs)/ (R₁ + 1/Cs)

The equivalent V_i (s) = R₂ + R₁(1/Cs)/ (R₁ + 1/Cs)

now we know that transfer function H(s) = V_o(s) / V_i(s)

= R₂ / [R₂ + R₁(1/Cs)/ (R₁ + 1/Cs)]

= R₂(R₁Cs + 1) / [R₁R₂Cs + 1/(R₁ + R₂)]

= R₂/(R₁ + R₂) (R₁Cs + 1) / [R₁R₂Cs/(R₁ + R₂) + 1]

Here T = R₁ C

A = R₂ / (R₁ + R₂)

H(s) = Vo(s) / Vi(s)

= A (Ts + 1) / (TAs + 1)

Pole = -1/AT

Zero = – 1/T

Phase angle(θ) = sin^-1(1 – A / 1 + A)
θ = 90 – 2tan^-1(A)1/2

Lag Compensator

In a control system, the lag compensator creates an output that is phase-late. Lag here refers to being behind or delayed. It is made up of one capacitor C and two resistors, designated R1 and R2.

Lag Compensator

An RC circuit is the result of the lag compensator diagram. The output’s connection over the second branch is seen quite clearly. It has a capacitor C linked in series with one resistor R2.

Thus, the circuit’s output is:

V_o(s) = R₂ + 1/Cs

V_i(s) = R₁ + R₂ + 1/Cs

Transfer Function = H(s) = V_o(s) / V_i(s)

= (R₂ + 1/Cs ) / (R₁ + R₂ + 1/ Cs)

= CsR₂ + 1 / (Cs(R₁ + R₂) + 1)

Lets A = R₂ + R₁

T = R₂C

So the required equation will be = H(s) = 1 + Ts / 1 + ATs

Pole = -1 / AT

Zero = – 1 / T

Phase angle (ϕ) = sin^-1 [(1 – A) / (1 + A )]

Lag-Lead Compensator

The lag-lead compensator is a mixture of a lag and a lead compensator, as the name suggests.

In a control system, the lag compensator creates an output that is phase-late. In a control system, the phase lead is used to produce the output by the lead compensator. As a result, the output of the lag-lead compensator has phase lead in one frequency area and phase lag in another.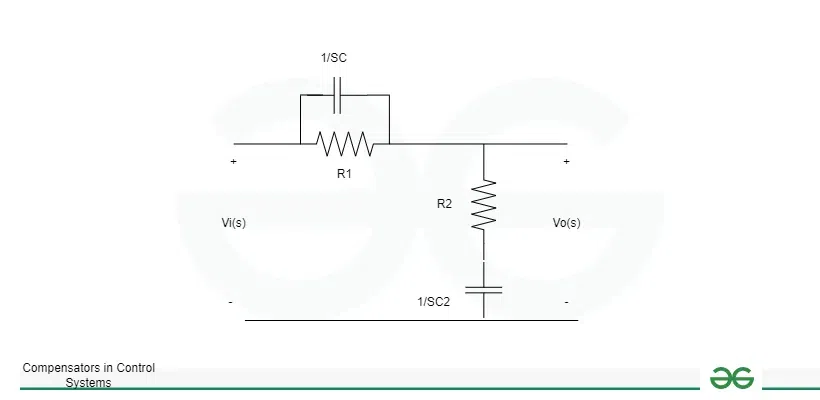

Lag – Lead Compensator

It is made up of two capacitors, C₁ and C₂, and two resistors, R₁ and R₂.

Transfer function = H(s) = V_o(s) / V_i(s)

The lag compensator diagram’s output shows that the output is connected across the second branch and is represented as an RC circuit. It has a capacitor, C₂, linked in series with one resistor, R₂.

V_o(s) = R₂ + 1/C₂s

Let’s find the input.

It will be:- R₂ + 1/C₂s

The parallel combination :- R₁ x 1/C₁s/(R₁ + 1/C₁s)

The series combination of the combinations mentioned before will now be the comparable input, and it is provided by:

V_i(s) = R₂ + 1/C₂s + R₁ (1/C₁s)/(R₁ + 1/C₁s)

Now the TS will be H(s)

Transfer function H(s) = V_o(s)/V_i(s)

=( R₂ + 1/C₂s) / {(R₂ + 1/C₂s) (R₁ + 1/C₁s) + R₁ x 1/C₁s}/ ((R₁ + 1/C₁s)

= (R₂ + 1/C₂s) (R₁ + 1/C₁s) / R₁R₂C₁C₂s + (R₁C₁ + R₂C₂ + R₁C₂)s + 1

Let, AT₁ = R₁C₁

BT₂ = R₂C₂

T₁T₂ = R₁R₂C₁C₂,

if AB = 1

H(s) = V_o(s)/V_i(s) = (1 + AT₁s) (1 + BT₂s) / (1 + T₁s) (1 + T₂s)

Gain Cross over point

The frequency at which the unity gain (zero dB line) and the magnitude response of the system’s open-loop transfer function intersect is known as the crossover point in control systems. This is a critical issue for control system design and stability analysis, especially when considering frequency domain analysis.

In most control systems, changing system parameters like gains, time constants, or the location of poles and zeros will give you control over the crossover point.

Frequency Response Analysis : Analyze the frequency response of the open-loop transfer function. This involves plotting the magnitude and phase response as a function of frequency.

Identify Crossover Point : Locate the frequency at which the magnitude response crosses 0 dB. This is the crossover frequency.

Difference Between Phase Lead and Phase Lag