Area of Triangle when measures of its three sides are given is found using Heron’s formula. The area of any two-dimensional shape is the measure of a region’s size on a surface. A triangle is a closed polygon having three sides and three vertices. Area of a triangle can be found using different methods. One of them includes determining the area using measures of the length of each side of the triangle.

In this article, we will discuss that method, the formula, and some solved examples based on the calculation of the area of a triangle with three sides.

What is the Area of a Triangle with 3 Sides Formula?

Area of Triangle with 3 sides is calculated using Heron’s Formula. The formula was given by a Greek Mathematician named Heron. The formula can be further extended to calculate area of quadrilaterals. Heron’s Formula for Area of Triangle with 3 sides is given as follows:

A = √{s(s-a)(s-b)(s-c)}

Where,

• A = Area of Triangle
• s = Semi-perimeter of Triangle
• a,b,c = Measure of Respective Sides of Triangle

Semi-perimeter of the triangle (s) is calculated as follows:

s = (a+b+c)/2

Proof of Formula for Area of Triangle with 3 Sides

Formula for Area of Triangle with 3 Sides can be derived two ways

• Using Pythagoras Theorem
• Using Law of Cosine

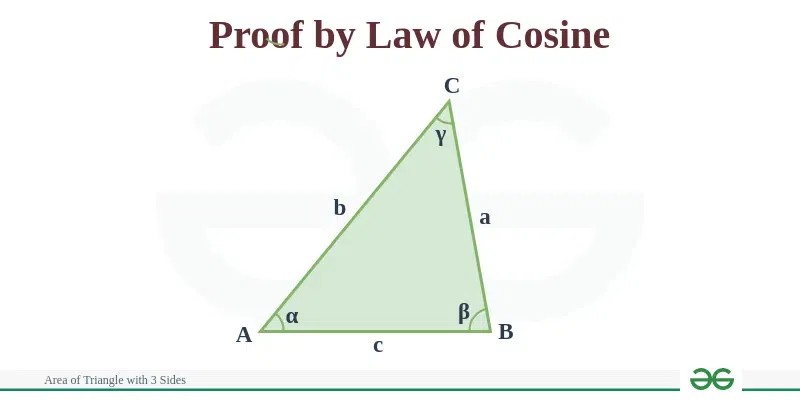
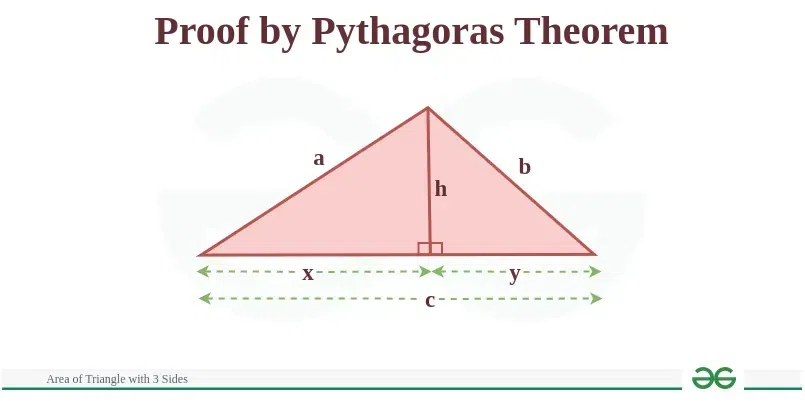
Let’s discuss these methods in detail as follows:

Area of Triangle with 3 Sides Formula Using Pythagoras Theorem

To prove Heron’s formula using the Pythagorean theorem, let’s consider a triangle with side lengths a, b, and c where c is the longest side. We’ll divide this triangle into two right triangles using an altitude from the vertex opposite the hypotenuse. Let’s denote the altitude as h and the two segments of the hypotenuse as x and y as the following diagram:

For the first right triangle, using pythagoras theorem

x² + h² = a²

⇒ h² = a² – x² . . .(i)

For the second right triangle, using pythagoras theorem

y² + h² = b²

⇒ h² = b² – y² . . .(ii)

From equation (i) and (ii), we get

a² – x² = b² – y²

⇒ a² – b² = x² – y² . . .(iii)

Now, let’s consider the segments of the hypotenuse:

c = x + y

⇒ c² = (x + y)²

⇒ c² = x² + y² + 2xy

From equation (iii),

c² = a² – b² + 2xy

⇒ 2xy = c² – a² + b²

Now, let’s find the area A of the triangle using the formula for the area of a triangle with base c and height h:

A = 1/2 × ch

[Tex]\Rightarrow A = \frac{1}{2}c \sqrt{a^2 – x^2} [/Tex]

[Tex]\Rightarrow A = \frac{1}{2}c \sqrt{a^2 – \left( \frac{c^2 – a^2 + b^2}{2} \right)} [/Tex]

[Tex]\Rightarrow A = \frac{1}{2}c \sqrt{\frac{2a^2 + 2b^2 – c^2}{2}} [/Tex]

[Tex]\Rightarrow A = \frac{1}{2}c \sqrt{2a^2 + 2b^2 – c^2} [/Tex]. . .(iv)

As we know, s = (a + b + c)/2

⇒ c = 2s – a – b

Putting c = 2s – a – b in equation (iv)

[Tex]A = \frac{1}{2}(2s – a – b) \sqrt{2a^2 + 2b^2 – (2s – a – b)^2} [/Tex]

[Tex] \Rightarrow A = \sqrt{s(s – a)(s – b)(s – c)} [/Tex]

Therefore, we have proven Heron’s formula using the Pythagorean theorem.

Area of Triangle with 3 Sides Formula Using Cosine Law

Heron’s Formula can be proved using the trigonometric law of cosines. For a ΔABC, let a, b, and c be the sides of the triangle and α, β, and γ be the angles opposite to the respective sides.

Then, using law of cosines, we get,

cos γ = (a²+b²-c²)/2ab

Using sinγ = √(1 – cos²γ), we get

sin γ = √{4a²b² – (a² + b² – c²)²}/2ab

We have,

• Base of the triangle = a
• Height of the triangle = b sinγ

We know that Area of triangle, A = 1/2 × Base × Height,

A = 1/2 × (ab sin γ)

⇒ A = 1/4 × √{4a²b² – (a² + b² – c²)²}

⇒ A = 1/4 × √{(2ab – (a² + b² – c²))*(2ab + (a² +b² -c²))}

⇒ A = 1/4 × √{(c² – (a-b)²)*((a+b)² – c²)}

⇒ A = 1/4 × √{(c-a+b)(c+a-b)(a+b+c)(a+b-c)}

Putting s = (a+b+c)/2, we get,

A = √{s(s-a)(s-b)(s-c)}

Thus, we have derived the formula for area of triangle with 3 sides using the trigonometric cosine rule and some basic mathematical identities.

How to Find Area of Triangle with 3 Sides?

Steps to calculate area of triangle with 3 sides are discussed as follows:

Step 1: Calculate perimeter of triangle as P = a+b+c

Step 2: Calculate semi-perimeter as s = P/2

Step 3: Using Heron’s formula, find the area as A = √{s(s-a)(s-b)(s-c)}

Step 4: Use appropriate units as mm², cm², etc.

Area of Triangle With 3 Equal Sides

For an equilateral triangle, all three sides are equal. Let’s denote the length of each side as a.

The semiperimeter s of the equilateral triangle is:

s = (a + a + a)/2 = 3a/2

So, using Heron’s formula:

[Tex] A = \sqrt{s(s – a)(s – a)(s – a)} [/Tex]

[Tex]\Rightarrow A = \sqrt{\frac{3a}{2}(\frac{3a}{2} – a)(\frac{3a}{2} – a)(\frac{3a}{2} – a)} [/Tex]

[Tex]\Rightarrow A = \sqrt{\frac{3a}{2}(\frac{a}{2})(\frac{a}{2})(\frac{a}{2})} [/Tex]

[Tex]\Rightarrow A = \sqrt{\frac{3a^4}{16}} [/Tex]

[Tex]\Rightarrow A = \frac{a^2\sqrt{3}}{4} [/Tex]

So, the area A of an equilateral triangle with side length a is given by the formula:

[Tex] \bold{A = \frac{a^2\sqrt{3}}{4}}[/Tex]

Comparison with Other Area Formulas

Following is a table discussing other formulas to find area of different triangles: