Line is a one-dimensional geometric shape, whose both sides extend to infinity. There are different types of lines in geometry, based on shape, orientation, and intersection. Let’s learn about the different types of lines in geometry and their applications in detail.

What is Line

Line is the combination of infinite points that extend to infinity in both directions. It is defined as a one-dimensional shape, having a length without any breadth.  

It is generally represented by a straight line with arrowheads on both ends. The arrowhead represents the indefinite extension.

What is Ray

A straight line that can extend infinitely in one direction and the other endpoint is fixed is called a ray. As a ray can be extended infinitely from one side. It has no defined length.

For example, if A is the endpoint and B is a point in the direction of the ray, it can be denoted as “ray AB” or simply “ray A”.

Illustration of a Ray and a Line Segment

What is Line Segment

The segments of a line having two endpoints are called the line segments. In other words, a line segment is a fractional part of a line

It is generally represented by any two points lying on the line with each point having some alphabetical name. For example, if two endpoints of line segments are A and B, then the line segment can be written just as AB.

Types of Lines

There are various different types of lines in geometry, having various different properties and characteristics. 

• Types of Line Based on Structure
  • Straight Lines
  • Curved Lines
  • Zig-Zag Lines
  • Broken Lines or Dash Lines
• Types of Line Based on Orientation 
  • Horizontal Lines
  • Vertical Lines
  • Diagonal Lines
• Types of Line Based on Intersection
  • Intersecting Lines
  • Bisecting Lines
  • Perpendicular Lines
  • Parallel Lines
  • Transversal Lines

Types of Lines Based on Shape

Based on the shape or change in direction, we can classify the lines as:

• Straight Lines
• Curved Lines
• Zig-Zag Lines
• Broken Lines or Dash Lines

Let’s discuss them in detail.

Straight Line

Straight Lines are those lines that do not deviate from a linear path even after extending to infinity length. These lines are characterized by having the same direction and no curvature at all.

We can extend straight lines indefinitely in both directions. A line has the same constant slope (the angle from the positive x-axis).

Straight Line and Curved Line Illustration

Curved Line

Curved lines are those lines that have a gradual change in their direction. Their slope changes gradually between different values. Unlike straight lines, they do not follow a linear path.

Curved Lines when closed can form various different geometric objects such as circles and ellipses, and when not closed makes curvature like spirals, arc, parabola, etc.

Zig Zag Line

Zig-zag lines are sharply pointed collections of line segments that have a sudden change in their slope. These lines are made up of a series of connected line segments that have a positive and negative slope in alternate order.

These lines resemble a sequence of “Z” or “N” shapes and form a jagged line. The major use case of  Zig-zag lines is in art and graphic design, where these lines are used to represent sudden rapid change or dynamic movement.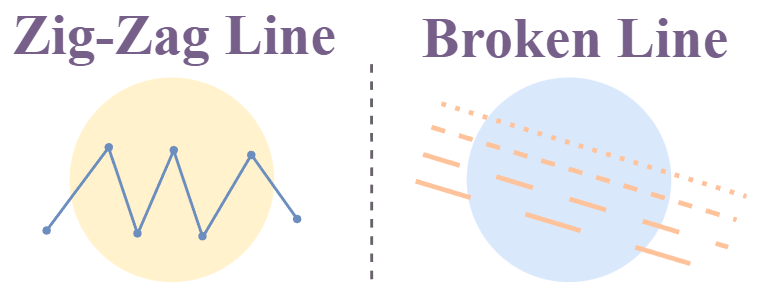

Illustration of Zig-Zag and Broken Lines

Broken Line

Broken lines are a collection of many tiny line segments that are arranged in a straight line, where the length of each line segment can vary depending on the use case.

They are also called dashed lines, as these line segments look like dash.

Types of Lines Based on Orientation 

• Horizontal Lines
• Vertical Lines
• Diagonal Lines

Let’s discuss them in detail.

Types of Lines Based on Orientation 

Horizontal Line

Horizontal lines are those lines, that are parallel to the horizontal axis i.e., the x-axis or the ground level. In other words, those lines which go from left to right or vice versa are called horizontal lines.

In algebra, we can represent the horizontal lines using the equation y = constant.

Vertical Line

Vertical lines are the opposite of the horizontal lines and are parallel to the verticle axis i.e., the y-axis. In other words, those lines which are perpendicular to the ground level are called vertical lines.

These lines go in the up and down direction and we can see these lines in the real world as poles, multi-floor buildings, columns to support structures, etc.

Diagonal Line

Diagonal lines are lines which are neither go in a horizontal direction nor in a vertical direction as these lines are at that slant whose slope lies between horizontal and vertical.

They are also called oblique lines. 

Types of Lines Based on Intersection

• Intersecting Lines
• Bisecting Lines
• Perpendicular Lines
• Parallel Lines
• Transversal Lines

Let’s discuss them in detail.

Intersecting Lines

Intersecting lines are two or more lines that meet or cross or intersect at a common point. The point where these lines meet is called the intersection point.

In algebra, this point of intersection is a solution to the system of equations formed by the two lines.

Illustration of Intersecting and Bisecting Lines

Bisecting Lines

Bisecting lines are those lines that divide a line segment into two equal parts. That object can be an angle, triangle, any polygon or a line segment. They pass through the midpoint of the object.

Bisecting lines are commonly used in geometry to divide angles or line segments equally.

Perpendicular Lines

Perpendicular lines are those intersecting lines that make a right angle with each other. One such pair of perpendicular lines are vertical and horizontal lines if they intersect. Also, the slope of perpendicular lines has a relationship with each other i.e., a product of the slope of perpendicular lines is always -1. For example, if one line has a slope of 2, the perpendicular line will have a slope of -1/2.

Representation of Perpendicular and Parallel Lines

Read More On:

• Perpendicular lines

Parallel Lines

Parallel lines are the opposite of intersecting lines i.e., they never intersect, no matter how far they are extended. All the parallel lines have the same slope but different y-intercepts.

In algebra, all the parallel lines have similar equations except the constant part. For example, the lines y = 2x + 1 and y = 2x – 3 are parallel.

Read More On:

• Parallel Lines

Transversal Lines

Transversal lines are those lines that intersect two or more other lines.

For two lines, transversal lines form 8 angles and in the case of parallel lines, these 8 angles show various properties and relationships. Some of these angles are corresponding angles, alternate interior angles, alternate exterior angles, and consecutive interior angles.

Illustration Of Transversal Line

Special Types of Lines

There are various special types of lines in geometry, which are:

1. Tangent Lines
2. Secant Lines
3. Skew Lines
4. Lines of Symmetry

Let’s discuss them in detail.

Tangent Line

Tangent lines are defined as those lines which only touch the curve or geometric object at one point and then never intersect again.

• At the point of contact tangent and curve have the same slope i.e.,

dy/dx if y = f(x) is the given curve.

• In the case of two dimensions, a tangent of any curve at any point represents the instantaneous rate of change which is the same as the slope.

Illustration of Tangent and Secant Lines

Secant Line

On the other hand, secant lines are different than tangent as these lines intersect the curve or geometric object such as a circle at two or more distinct points. There are some properties of secant lines with respect to the circle which is called “tangent secant theorem” and “alternate secant theorem”.

Skew Line

In three-dimensional space, skew lines are those pair of lines that neither intersect nor parallel to each other. They are not defined for two dimensions.

Line of Symmetry

A line of symmetry is the line that divides a shape into two congruent halves. The two halves are the mirror image of each other. Due to this fact, the line of symmetry is also called a mirror line.

This concept is applied to various geometric shapes, including polygons, letters, and objects.

Read More:

• Lines and Angles
• Types of Angles
• Points, Lines, and Planes

FAQs on Types of Lines

What is Line?

A line is a straight path that extends infinitely in both directions. It has no endpoints and is often represented using a straight line with arrows at both ends. A line can be thought of as a collection of points that extend indefinitely in both directions.

Define Ray.

A ray is a straight line that extends infinitely in one direction from a specific starting point called the endpoint. It has no defined endpoint in the other direction and continues indefinitely.

Define Line Segment.

A line segment is a straight path between two points in space. It consists of the endpoints and all the points lying between them. Unlike a line, a line segment has a defined length and can be measured.

What is the Difference between Line and Line Segment?

A line is infinitely long with no endpoints, while a line segment has two distinct endpoints.

How Many Types of Lines are there in Geometry?

Various types of lines, based on various different parameters are,

• Straight Lines
• Curved Lines
• Zig-Zag Lines
• Broken Lines or Dash Lines
• Horizontal Lines
• Vertical Lines
• Diagonal Lines
• Intersecting Lines
• Bisecting Lines
• Perpendicular Lines
• Parallel Lines
• Transversal Lines

What is Perpendicular Line?

A perpendicular line is a line that forms a 90-degree angle with another line or surface. If two lines intersect and the angles formed are all 90 degrees, they are said to be perpendicular to each other.

What are Parallel Lines?

Parallel lines are lines that lie in the same plane and never intersect, no matter how far they are extended. They have the same slope and will always maintain the same distance apart.

Do Parallel Lines Meet?

No, parallel lines never meets, even we extend those lines to infinite distance then also they never meet.

What is Intersecting Line?

An intersecting line is a line that crosses or meets another line at a specific point called the point of intersection. When two lines intersect, they share a common point.

What is Transversal Line?

Transversal line is a line that intersects two or more other lines at different points. It forms various angles with the intersected lines, such as corresponding angles, alternate interior angles, and alternate exterior angles.

What is Skew Line?

Skew lines are lines that do not lie in the same plane and are neither parallel nor intersecting. They are non-coplanar lines that maintain a constant distance between each other while moving in space.

What is Tangent Line?

A tangent line is a line that touches a curve or surface at a single point and does not intersect it further. It represents the instantaneous direction of the curve at that point.

What are Concurrent Lines?

Concurrent lines are three or more lines in a plane that intersect at a single point. This common point of intersection is known as the point of concurrency.