Determinant of a 2×2 Matrix A = [Tex]\begin{bmatrix} a&b \\ c&d \\ \end{bmatrix} [/Tex] is denoted as |A| and is calculated as |A| = [ad – bc]. It is used in solving various problems related to a matrix and is used in finding the Inverse, and Rank of 2×2 Matrix.

In this article, we will learn about, the Determinant of Matrix, Determinant of 2×2 Matrix, Examples, and others in detail.

What is Determinant of a Matrix?

In linear algebra, the determinant is a scalar value that is associated with a square matrix. Among the important information provided by the matrix are its singularity and invertibility and we can find using determinant whether any matrix is singular or invertible.

Notation det(A) or |A| represents the determinant of a matrix A.

Now determinant is only calculated for any square matrix and the determinant for any 2×2 matrix is calculated below,

For 2×2 Matrix

[Tex]\begin{bmatrix} a&b \\ c&d \\ \end{bmatrix} [/Tex]

Determinant is calculated as:

det (A) = ∣A∣ = ad − bc

For 3×3 Matrix

[Tex]\begin{bmatrix} a&b&c \\ d&e&f\\ g&h&i \end{bmatrix} [/Tex]

Determinant is calculated using a more complex formula:

det (B) = ∣B∣ = a(ei − fh) − b(di − fg) + c(dh − eg)

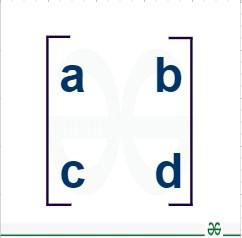
What is 2 × 2 Matrix?

Any square matrix of 2 rows and 2 columns is called a 2 × 2 Matrix. In a 2 × 2 Matrix we have a total of 4 elements. A 2 × 2 matrix is represented below as,

2×2 Matrix

Learn, Matrices

Determinant of a 2×2 Matrix

Determinant of 2×2 matrix is the single scalar value of a matrix of order 2. For any given matrix A_2×2 given as follows

[Tex]A~=~\begin{bmatrix}a&b \\ c&d \\\end{bmatrix} [/Tex]

The determinant of the matrix can be found using the following formula

Determinant of 2×2 Matrix Formula

Following formula provides the determinant of a 2×2 matrix:

det(A) = |A| = ad – bc

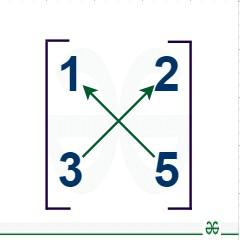
Product of the elements on the major diagonal (which runs from top left to bottom right) less the product of the elements on the other diagonal is the determinant for the matrix ￰ A.

|A| = (a⋅d) − (b⋅c)

How to Calculate Determinant of a 2×2 Matrix

To calculate the determinant of a 2×2 matrix:

A = [Tex]\begin{bmatrix} a&b \\ c&d \\ \end{bmatrix} [/Tex]

Use this Formula to calculate Determinant of a 2×2 Matrix

det(A) = ∣A∣ = ad − bc

For further follow the following steps,

Step 1: To find a⋅d, multiply the components on the major diagonal (from top left to bottom right).

Step 2: To get b⋅c, multiply the items on the opposite diagonal (from top right to bottom left).

Step 3: Deduct the outcome from step 2 from the outcome from step 1.

Step 4: Result is the determinant of the 2×2 matrix is equal to A.

Example: Suppose we have to find determinant of [Tex]A = \begin{bmatrix} 0&1 \\ -1&2 \\ \end{bmatrix} [/Tex]

Given Matrix,

To find its determinant we cross-multiply its components, such as,

Determinant of Matrix Formulas

Determinant of any matrix can easily be claulated using the Determinnat Formulas, For any 2×2, 3×3, or any n×n matrices its deteminat is calculated below,

Determinant of 2×2 Matrix

For a 2×2 matrix

[Tex]A~=~\begin{bmatrix} a&b \\ c&d \\ \end{bmatrix} [/Tex]

det(A) is given by:

det(A) = ad − bc

Example: Find determinant of [Tex]A~=~\begin{bmatrix} 1&2 \\ 3&4 \\ \end{bmatrix} [/Tex]

Solution:

Determinant of A = |A|

|A| = (1.4) – (2.3)

|A| = 4 – 6

Determinant of 3×3 Matrix

For a 3×3 matrix

A = [Tex]\begin{bmatrix} a&b&c \\ d&e&f\\ g&h&i \end{bmatrix} [/Tex]

Determinant is given by

det(A) = a(ei-fh) – b(di-fg) + c(dh-eg)

Example: Find determinant of [Tex]\begin{bmatrix} 1&2&3 \\ 4&5&6\\ 7&8&9 \end{bmatrix} [/Tex]

Solution:

Determinant of A = |A|

|A| = 0

Learn more about, Determinant of 3×3 Matrix

Determinant of a n×n Matrix

When calculating the determinant of a n×n matrix ￰(n > 3), more intricate calculations are required. Typically, techniques like cofactor expansion, expansion by minors, or block matrix characteristics are used. Recursive in nature, the general formula can be somewhat complex.

A popular method is to write the determinant as the product of elements and the cofactors that go with them.

[Tex]\text{det}(C) = \sum_{j=1}^{N} (-1)^{i+j} \cdot c_{ij} \cdot \text{det}(C_{ij}) [/Tex]

where the element in the i-th row and j-th column of matrix C is represented by the symbol C_ij.

Determinant of Inverse of a Matrix

If A is an invertible matrix, then the determinant of its inverse A^-1 is given by the formula,

det(A^-1) = 1/det(A)

Learn more about, Inverse of Matrix

Properties of Determinant of Matrix

It is essential to comprehend the characteristics of determinants. Among the essential characteristics are:

• Determinant of kA, where k is a scalar, is equal to k^n times det(A), assuming that matrix A has a determinant of det(A).

• Determinant of a matrix and its transpose are equal: det(A) = det(A^T)

• A matrix’s determinant is 0 if it contains zeros in either its row or column.

• Determinant of a matrix is 0 if two of its rows or columns are proportionate.

• A matrix’s determinant is 0 if it is singular (non-invertible).

• Transpose Property: A matrix’s transpose’s determinant and its original matrix’s determinant are the same.

• Product of Matrices: Product of the determinants of two matrices is the determinant of the product of those matrices.

Application of Determinant of 2×2 Matrix

Application of determinat of 2×2 Matrix are,

• It is used to mind inverse of 2×2 Matrix.

• It is used in solving linear equation using Cramer’s Rule.

• It is used in various mathematical computation.

Read More,

• Types of Matrices
• Matrix Operations
• System of Linear Equations with Three Variables

Examples of Determinant of 2×2 Matrix

Some examples on Determinant of 2×2 Matrix are,

Example 1: Find the determinant of 2×2 Matrix A

[Tex]A~=~\begin{bmatrix} 2 & 3 \\ 4 & 1 \\ \end{bmatrix} [/Tex]

Solution:

Using the formula:

det(A) = ad − bc

det(A) = (2×1) − (3×4) = 2 − 12 = −10

So, for this matrix A, the determinant is −10

Example 2: Find the determinant of 2×2 Matrix B

[Tex]B~=~\begin{bmatrix} -1& 0 \\ 2&5 \\ \end{bmatrix} [/Tex]

Solution:

Using the formula:

det(B) = (−1×5) − (0×2) = −5

So, for matrix B, the determinant is −5

Example 3: Consider the 2×2 matrix

[Tex]A~=~\begin{bmatrix} 3&1 \\ 2&4 \\ \end{bmatrix} [/Tex]. Find its Determinant.

Solution:

Determinant of Matrix,

denoted as det(A) or ∣A∣, is calculated using formula:

det(A) = (3×4) − (2×1) = 12 − 2 = 10

So, for matrix, det(A)=10

Example 4: Take Matrix

[Tex]B~=~\begin{bmatrix} -1 &2 \\ 0& 5\\ \end{bmatrix} [/Tex]. Find its Determinant.

Solution:

Determinant of matrix B is calculated as follows:

det(B) = (−1×5)−(0×2) = −5

Thus, det(B) = −5

Example 5: Take Matrix

[Tex]C~=~\begin{bmatrix} 4&0 \\ -3& 7\\ \end{bmatrix} [/Tex]. Find its determinant.

Solution:

Using Determinant Formula:

det(C) = (4×7)−(−3×0) = 28

So, det(C) = 28

Determinant of 2×2 Matrix – FAQs

How do you Find Determinant of a 2×2 Matrix?

To find the determinant of a 2×2 matrix A = [a, b: c, d] is |A| = [ad – bc]. It is found by multiplying cross element from top left and then subtracting the product.

What Function do Determinants Serve in Algebra?

Determinants are essential for solving systems of linear equations because they disclose important information about a matrix, such as its invertibility.

Do Negative Determinants Ever Exist?

In some situations, the determinants of a matrix can be negative. For a 2×2 matrix, the sign is determined by the arrangement of the elements.

Are There Any Other Ways to Compute Determinants?

There are a number of techniques, such as employing eigenvalues, cofactor expansion, and expansion by minors.

How do You Solve a 2×2 Determinant?

To solve the 2×2 det cross multiply the elements and find their difference.