Alternate Angles are a concept in geometry that arise when two lines are crossed by another line (known as the transversal). There are two types of alternate angles i.e., Alternate Interior Angles and Alternate Exterior Angles. Alternate angles are formed when a line intersects two or more lines, and if these lines are parallel, then alternate angles are equal.

In this article, we will explore the concept of alternate angles, including Alternate Interior Angles and Alternate Exterior Angles. We will also delve into the theorems related to these angles and provide proofs for them.

What are Alternate Angles?

Alternate angles are a type of angle in geometry that serves as the foundation for comprehending ideas related to angles and parallel lines. Alternate angles are created on either side of a transversal that passes through two or more parallel lines.

These angles are never contiguous. In this post, we will go over the appropriate definition of Alternate Angles, as well as the kinds, theorems, and some sample problems on alternate angles.

Alternate Angles Definition

Alternate angles are pairs of angles formed when a transversal crosses two lines, located on opposite sides of the transversal but inside the two lines and non-adjacent to each other.

Alternate angles (interior), are often referred to as “Z angles” due to the Z-shape formed when a transversal intersects two parallel lines. These angles are congruent, meaning they have equal measures, when the lines are parallel. This property is a fundamental aspect of geometric proofs and problems.

Properties of Alternate Angles

• The total of the angles created on the same transverse side that are inside the two parallel lines is 180°.
• Two non-parallel lines can likewise be used to create alternate angles, however the angles created in this manner are unrelated.
• A Z-shaped figure has two alternate internal angles that are easily distinguished from one another. These angles are also known as Z-angles.
• When it comes to non-parallel lines, alternate interior angles are the same.

How to Calculate Alternate Angles?

To compute with alternate angles:

• Highlight the angles you are already familiar with.
• To identify a missing angle, use other angles.
• Use a basic angle fact to get the missing angle.

Types of Alternate Angles

The alternative angles are grouped into two sorts based on the location of the angles, namely

• Alternate Interior Angles 
• Alternate Exterior Angles 

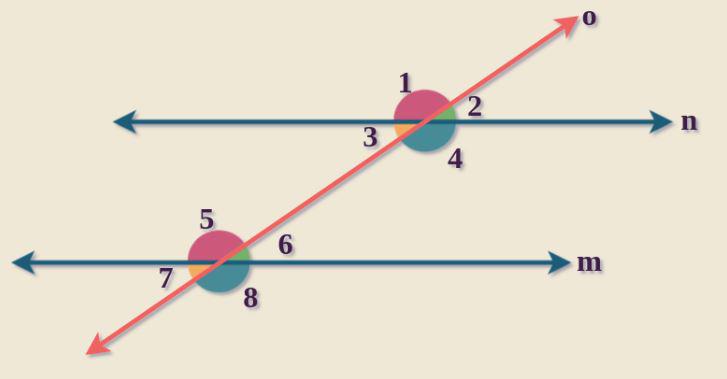
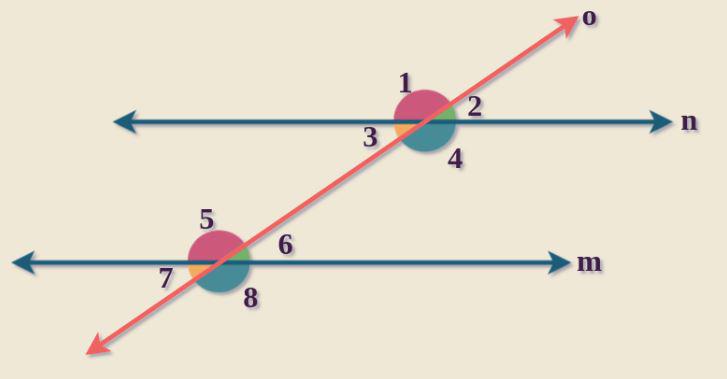
Alternate Interior Angles

The pair of angles on the inner side of the two parallel lines but on the opposite side of the transversal is known as an alternate interior angle. When two lines are crossed by a third line, alternate internal angles are generated. The third line is known as the transversal line.

When two parallel or non-parallel lines are crossed by a transversal line, alternate interior angles are always created. The angles are on opposing sides of the transversal line and on the inside of parallel or non-parallel lines.

With the same image as previously, we can observe that pairs of opposing interior angles are represented by ∠3 & ∠6 and ∠4 & ∠5.

Alternate Exterior Angles

Alternate exterior angles are the pair of angles on the outside of the two parallel lines but on the other side of the transversal. A transversal is a line formed by the intersection of two or more parallel lines.

When a transversal is made over parallel lines, several pairs of angles are formed. When a transversal intersects two parallel lines, it creates four interior angles on the inside and four external angles on the outside.

With the same image as previously, we can observe that pairs of opposing exterior angles are represented by ∠1 & ∠8 and ∠2 & ∠7.

Alternate Angles Theorems

According to the alternative angle theorem, alternate interior angles or alternate exterior angles that come from crossing two parallel lines by a transversal are congruent.

To Show:

When transversal cuts two or more parallel lines, the alternative angles created are always congruent.

Proof:

Consider the two coplanar parallel lines m and n shown in the image above. When a line o intersects these two parallel lines m and n, the figure tends to create particular angles with regard to the lines.

At the place where the straight lines n and o cross,

 ∠3 +  ∠4 = 180° (the straight line is n)—-(1)

 ∠2 +  ∠4 = 180° (the straight line is o)—-(2)

So, by combining (1) and (2), we obtain

∠2 = ∠3

Again, at the place where the straight lines m and o cross,

 ∠5 +  ∠6 = 180° (the straight line is m).—-(3)

 ∠8 +  ∠6 = 180° (the straight line is o).—-(4)

So, by combining (3) and (4), we obtain

∠5 = ∠8

In the picture above:

∠2 =∠6 and ∠4 = ∠8 (Corresponding angles)

This means that ∠3 =∠6 and ∠4 = ∠5, where ∠3, ∠4, ∠5, and ∠6 are alternative angles.

As a result, opposite angles are either congruent or equal.

Alternate Interior Angles Theorem

Alternate interior angles are the angles on the inner side of the two parallel lines but on the other side of the transversal.

When a transversal intersects two parallel lines, the resulting pairs of alternative interior angles are congruent.

Proof of Alternate Interior Angles Theorem

Given: Lines AB and CD are parallel.

To prove: ∠4 = ∠6 and ∠3 = ∠5

Proof: Suppose that a transversal, Y, crosses the parallel lines AB and CD. One special property of the parallel lines is that certain angles line up when a transversal passes across them.

In other words, comparable angles and vertically opposed angles become equal when a transversal joins parallel lines.

Taking this into consideration:

∠1 = ∠6 [Corresponding angles], and

∠1 = ∠4 [Vertically opposite angles]

Therefore, by comparing these relationships:

∠4 = ∠6 [Alternate interior angles]

Similarly,

∠3 = ∠5

As a result, it has been demonstrated that some pairings of angles on parallel lines cut by a transversal, such as ∠4 and ∠6, and ∠3 and ∠5, are truly equal!

Read More about Alternate Interior Angles.

Alternate Exterior Angles Theorem

The pair of angles on the outer side of the two parallel lines but on the other side of the transversal are known as alternate exterior angles.

When a transversal intersects two parallel lines, the resulting pairs of alternative exterior angles are congruent.

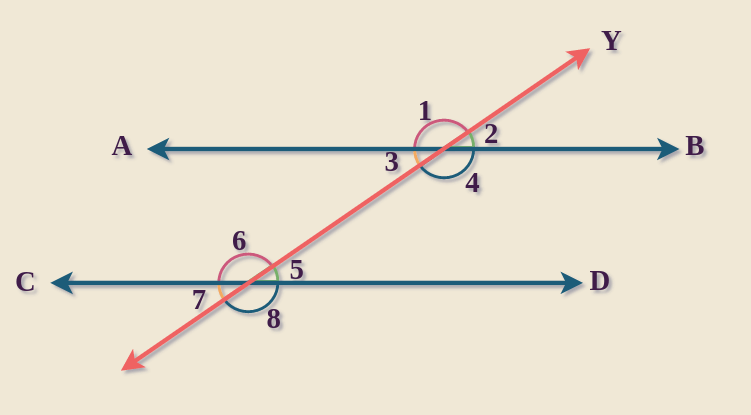
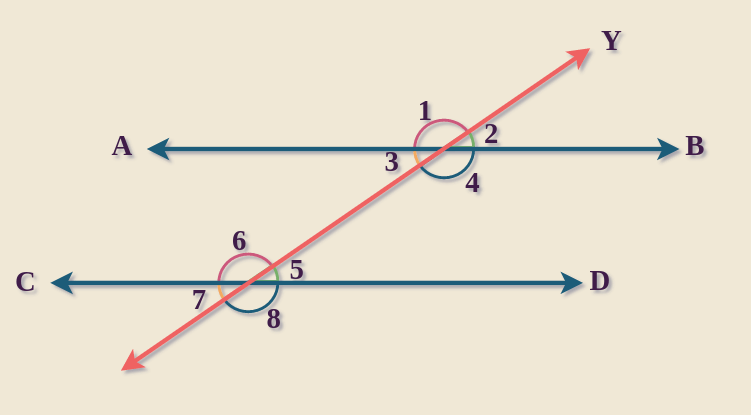
Proof of Alternate Exterior Angles Theorem

Given: Parallel lines AB and CD are crossed by transversal Y.

[Hint: We’ll apply the following axioms: When lines are parallel, their corresponding angles are congruent, and when corresponding angles are congruent, the lines are parallel.]

To prove: ∠1 = ∠8

Proof: Let’s investigate the link between these angles by looking at their relationships to other angles. ∠1 and its vertically opposite ∠4 create a critical relationship.

Knowing that ∠1 corresponds to ∠4 (due to vertical angles) and that lines AB and CD are parallel:

∠4 corresponds to ∠8 (corresponding angles axiom).

As a result, by clicking on this link:

Because of transitivity, ∠1 equals ∠8.

As a result, ∠1 and ∠8 on parallel lines cut by transversal Y are definitely equal!

Read more about Alternate Exterior Angles.

Alternate Angles and Corresponding Angles

Angles generated by a transversal intersecting two lines are known as alternate angles and matching angles. Here are the major differences between them, as shown in a table: