Quadratic Inequalities	Meaning
3x2 + 2x ≠ 0	3x2 + 2x is not equal to zero
5x2 + 2x > 0	5x2 + 2x is greater than zero
x2 – 2x < 9	x2 – 2x is less than 9
x2 – 7x ≥ 2	x2 – 7x is greater than or equal to 2
x2 – 3x ≤ 5	x2 – 3x is less than or equal to 5

How to solve Quadratic Inequality?

We can solve a Quadratic Inequality using following steps:

Step 1. Set the quadratic expression: Write the quadratic inequality in the form ax² + bx + c < 0, > 0, ≤ 0, or ≥ 0.

Step 2. Factor or find roots: Factorize the quadratic expression or use the quadratic formula to find the roots (if possible).

Step 3. Determine critical points: Identify critical points or values of ‘x’ where the inequality may change, considering the roots and the sign of ‘a’.

Step 4. Create intervals: Use critical points to create intervals on the number line, dividing it into sections where the inequality might change.

Step 5. Choose test values: Select test values within each interval to check the inequality’s validity. Use values like endpoints, zeros, or convenient numbers within each interval.

Step 6. Evaluate the inequality: Substitute the test values into the original inequality to determine if they satisfy the inequality.

Step 7. Determine solution regions: Identify intervals where the inequality holds true based on the test values’ outcomes.

Step 8. Express solution set: Present the solution set either as an inequality on the number line or in set notation, considering the intervals where the inequality is valid.

Solve Quadratic Inequalities

Solving Quadratic Inequalities means finding the value of x for which it satisfies the given inequality. We can solve a Quadratic Inequality using three methods:

• Graphical Method
• Algebraic Method

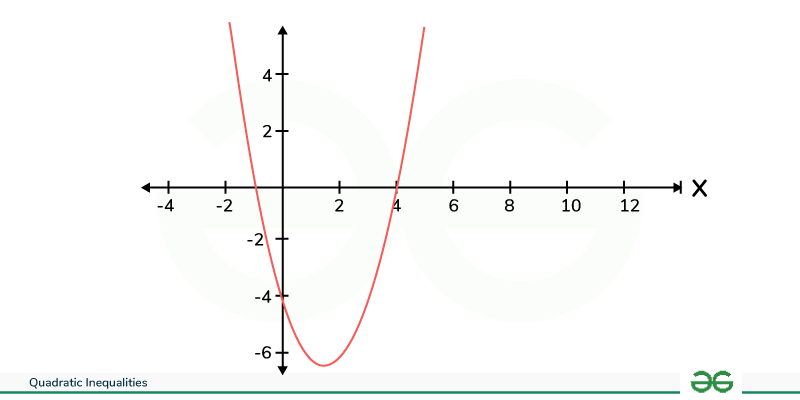
Graphical Method

In Graphical Method, we first draw the graph of the inequality and then find the solution of the given inequality using the graph. Lets see how to solve Quadratic Inequalities using the Graphical method with the help of an example.

Example: x² – 3x – 4 > 0

Solution:

We can solve the above example using graphical methods

Step 1: Plotting the graph of the quadratic function y = x² – 3x – 4

Finding the x-intercepts:

Given quadratic function: y = x² – 3x – 4

To find the roots, solve for y = 0:

x² – 3x – 4 = 0

Factorizing the equation or using the quadratic formula:

x² – 4x + x – 4 = 0

x(x – 4) + 1(x – 4) = 0

(x – 4)(x + 1) = 0

Therefore, the roots are x = 4 and x = -1

Plotting the graph:

Step 2: Identifying regions where the graph lies above the x-axis (where y > 0)

We are looking for the regions where the quadratic function is positivee(y > 0).

The function is y = x² – 3x – 4. We know the roots are x = 4 and x = -1.

Step 3: Determining the x-values within these regions to obtain the solution set

Based on the graph, the regions where y > 0 are:

– x < -1

– x > 4

Therefore, the solution set for x² – 3x – 4 > 0 is x < -1 or x > 4.

This solution is derived from observing the parts of the graph where the quadratic function y = x² – 3x – 4 is above the x-axis. 

Algebraic Method

Algebraically we can solve a quadratic inequality using following three methods

• Factoring
• Quadratic Formula
• Completing the Square

Factoring

In Factoring, we split the given quadratic expression in product of its factors to find out the solution.

Example: Find out the solution for the inequality x² – 3x – 4 > 0 using Factoring Method

Solution:

Given inequality: x² – 3x – 4 > 0

Step 1: Factor the quadratic expression:

(x – 4)(x + 1) > 0

Step 2: Identify intervals based on the factors:

Interval I: x < -1

For x < -1, consider the factors (x – 4)(x + 1):

Pick a test point within the interval, say x = -2, substitute into (x – 4)(x + 1):

((-2) – 4)((-2) + 1) = (-6)(-1) = 6 > 0

The inequality holds for x < -1.

Interval II: -1 < x < 4

For -1 < x < 4, consider the factors (x – 4)(x + 1):

Pick a test point within the interval, say x = 0, substitute into (x – 4)(x + 1):

(0 – 4)(0 + 1) = (-4)(1) = -4 < 0

The inequality doesn’t hold for -1 < x < 4.

Interval III: x > 4

For x > 4, consider the factors (x – 4)(x + 1):

Pick a test point within the interval, say x = 5, substitute into (x – 4)(x + 1):

(5 – 4)(5 + 1) = (1)(6) = 6 > 0

The inequality holds for x > 4.

Therefore, the solution is x < -1 or x > 4.

Quadratic Formula

Use the quadratic formula to find the roots and determine the intervals where the expression is positive.

Example: Find the solution of the given inequality x² – 3x – 4 > 0 using Quadratic Formula

Solution:

Step 1: Apply the quadratic formula to find the roots:

x = [3 ± √((-3)² – 4×1×(-4))]/(2×1)

x = [3 ± √(25)]/2

x = [3 ± 5]/2

Roots: x = 4 or x = -1

Step 2: Test intervals to determine where the expression is positive:

Interval I: x < -1 → (x² – 3x – 4) > 0

For x < -1, consider the quadratic expression (x² – 3x – 4):

Choose a test point, say x = -2, substitute into (x² – 3x – 4):

((-2)² – 3(-2) – 4) = (4 + 6 – 4) = 6 > 0

The inequality holds for x < -1.

Interval II: -1 < x < 4 → (x² – 3x – 4) < 0

For -1 < x < 4, consider the quadratic expression (x² – 3x – 4):

Choose a test point, say x = 0, substitute into (x² – 3x – 4):

((0)² – 3(0) – 4) = (-4) < 0

The inequality doesn’t hold for -1 < x < 4.

Interval III: x > 4 → (x² – 3x – 4) > 0

For x > 4, consider the quadratic expression (x² – 3x – 4):

Choose a test point, say x = 5, substitute into (x² – 3x – 4):

((5)² – 3(5) – 4) = (25 – 15 – 4) = 6 > 0

The inequality holds for x > 4.

Therefore, the solution is x < -1 or x > 4.

Completing the Square

In completing the square method, convert the quadratic expression into a perfect square trinomial to solve the inequality.

Example: Solve the given inequality x² – 3x – 4 > 0 by using Completing the Square Method

Solution:

Step 1: Complete the square:

x² – 3x – 4 = (x – (3/2))² – 25/4

Step 2: Set up the inequality:

(x – (3/2))² – 25/4 > 0

Step 3: Find the intervals where the inequality holds:

This gives two cases:

Case 1: x – (3/2) > 5/2

x > 8/2

x > 4

Case 2: x – (3/2) < -5/2

x < -2/2

x < -1

Therefore, the solution is x < -1 or x > 4.

Graphical Quadratic Inequalities

Graphing quadratic inequalities involves plotting the corresponding quadratic function and shading the region where the inequality holds true on the coordinate plane. The graph visually represents the solution set of the inequality.

To graph a quadratic inequality, first, plot the quadratic function y = ax² + bx + c on the Cartesian plane. Determine the concavity based on the sign of ‘a’. If ‘a’ is positive, the parabola opens upwards, and if ‘a’ is negative, it opens downwards. Locate the vertex of the parabola, determined by (-b/2a, f(-b/2a)), where ‘f’ represents the function.

Next, identify the critical points or roots (x-intercepts) of the quadratic equation, as they define the intervals that determine the solution set. Test a value within each interval to determine the regions that satisfy the inequality. Shade the appropriate area on the graph according to whether the inequality holds true within those intervals.

For example, if the inequality is of the form ax² + bx + c < 0 or ax² + bx + c > 0, shade the region where the parabola is below or above the x-axis, respectively. If it’s ax²+ bx + c ≤ 0 or ax² + bx + c ≥ 0, include points on the parabola itself.

The graph provides a clear visualization of the solution set of the quadratic inequality, aiding in understanding its solution regions on the coordinate plane.

Also Check

• Linear Inequalities
• Graphical Solution of Linear Inequalities in Two Variables
• Roots of Quadratic Equations

Quadratic Inequalities – Solved Examples

Example 1. Solve the inequality: x² – 4x + 3 > 0.

Solution:

Given inequality: x² – 4x + 3 > 0

Step 1: Factorize the quadratic expression:

x² – 4x + 3 = (x – 3)(x – 1) > 0

Step 2: Find intervals where the expression is positive:

Interval I: x < 1

For x < 1, consider the factors (x – 3)(x – 1):

Pick a test point, say x = 0, substitute into (x – 3)(x – 1):

(0 – 3)(0 – 1) = (-3)(-1) = 3 > 0

The inequality holds for x < 1.

Interval II: 1 < x < 3

For 1 < x < 3, consider the factors (x – 3)(x – 1):

Pick a test point, say x = 2, substitute into (x – 3)(x – 1):

(2 – 3)(2 – 1) = (-1)(1) = -1 < 0

The inequality doesn’t hold for 1 < x < 3.

Interval III: x > 3

For x > 3, consider the factors (x – 3)(x – 1):

Pick a test point, say x = 4, substitute into (x – 3)(x – 1):

(4 – 3)(4 – 1) = (1)(3) = 3 > 0

The inequality holds for x > 3.

Therefore, the solution is x < 1 or x > 3.

Example 2. Solve the inequality: x² + 2x – 15 ≤ 0.

Solution:

Given inequality: x² + 2x – 15 ≤ 0

Step 1: Factorize the quadratic expression:

x² + 2x – 15 = (x + 5)(x – 3) ≤ 0

Step 2: Find intervals where the expression is non-positive:

Interval I: -5 ≤ x ≤ 3

For -5 ≤ x ≤ 3, consider the factors (x + 5)(x – 3):

Pick a test point within the interval, say x = 0, substitute into (x + 5)(x – 3):

(0 + 5)(0 – 3) = (5)(-3) = -15 ≤ 0

The inequality holds for -5 ≤ x ≤ 3.

Therefore, the solution is -5 ≤ x ≤ 3.

Example 3. Solve the inequality: 2x² – 5x + 2 > 0.

Solution:

Given inequality: 2x² – 5x + 2 > 0

Step 1: Factorize the quadratic expression:

2x² – 5x + 2 = (2x – 1)(x – 2) > 0

Step 2: Find intervals where the expression is positive:

Interval I: x < 1/2

For x < 1/2, consider the factors (2x – 1)(x – 2):

Pick a test point within the interval, say x = 0, substitute into (2x – 1)(x – 2):

(2×0 – 1)(0 – 2) = (-1)(-2) = 2 > 0

The inequality holds for x < 1/2.

Interval II: x > 2

For x > 2, consider the factors (2x – 1)(x – 2):

Pick a test point within the interval, say x = 3, substitute into (2x – 1)(x – 2):

(2×3 – 1)(3 – 2) = (5)(1) = 5 > 0

The inequality holds for x > 2.

Therefore, the solution is x < 1/2 or x > 2.

Example 4. Solve the inequality: 3x² – 4x – 4 ≤ 0.

Solution:

Given inequality: 3x² – 4x – 4 ≤ 0

Step 1: Factorize the quadratic expression:

3x² – 4x – 4 = (3x + 2)(x – 2) ≤ 0

Step 2: Find intervals where the expression is non-positive:

Interval I: -2/3 ≤ x ≤ 2

For -2/3 ≤ x ≤ 2, consider the factors (3x + 2)(x – 2):

Pick a test point within the interval, say x = 0, substitute into (3x + 2)(x – 2):

(3×0 + 2)(0 – 2) = (2)(-2) = -4 ≤ 0

The inequality holds for -2/3 ≤ x ≤ 2.

Therefore, the solution is -2/3 ≤ x ≤ 2.

Example 5. Solve the inequality: x² + 6x + 9 > 0

Solution:

Given inequality: x² + 6x + 9 > 0

Step 1: Factorize the quadratic expression:

x² + 6x + 9 = (x + 3)(x + 3) > 0

Step 2: Find intervals where the expression is positive:

Interval I: x > -3

For x > -3, consider the factor (x + 3)^2:

For any value of x greater than -3, (x + 3)^2 will always be greater than zero because it represents a square value.

Therefore, the solution is x > -3.

Quadratic Inequalities – Practice Questions

Q1. Solve the inequality: 2x² – 7x + 3 < 0

Q2. Solve the inequality: x² + 4x + 4 ≥ 0

Q3. Solve the inequality: 4x² – 12x – 3 > 0

Q4. Solve the inequality: 5x² – 8x + 3 ≤ 0

Q5. Solve the inequality: 3x² + 5x – 2 > 0

Quadratic Inequalities – FAQs

What are Quadratic Inequalities?

Inequalities involving quadratic expressions (ax² + bx + c) with inequality signs.

How do you Solve Quadratic Inequalities?

Quadratic Inequalities can be solved by factoring, using the quadratic formula, or graphically interpreting solutions.

What is the Significance of Roots in Quadratic Inequalities?

Roots in Quadratic Inequalities identify critical points where the inequality may change direction.

Can Quadratic Inequalities have no Real Solutions?

Yes, if the quadratic expression does not intersect the x-axis.

Why do we Graph Quadratic Inequalities?

Graphing Quadratic Inequalities helps to visualize regions where the inequality holds true on the coordinate plane.

How to determine the Solution Intervals in Quadratic Inequalities?

To determine the the solution interval we first have to solve the equation and then determine the interval as per the inequality symbol

Can a Quadratic Inequality have Infinite Solutions?

Yes, if the inequality holds true for all values in its domain.

How do Quadratic Inequalities relate to Quadratic Equations?

Solutions of quadratic equations can help find intervals in quadratic inequalities.

What is the difference between Quadratic Equation and Quadratic Inequality?

The basic difference between Quadratic Equation and Quadratic Inequality is a quadratic equation uses equal to sign while quadratic inequality uses inequalities signs such as ≠, <, ≤, >, ≥ between right hand and left hand values