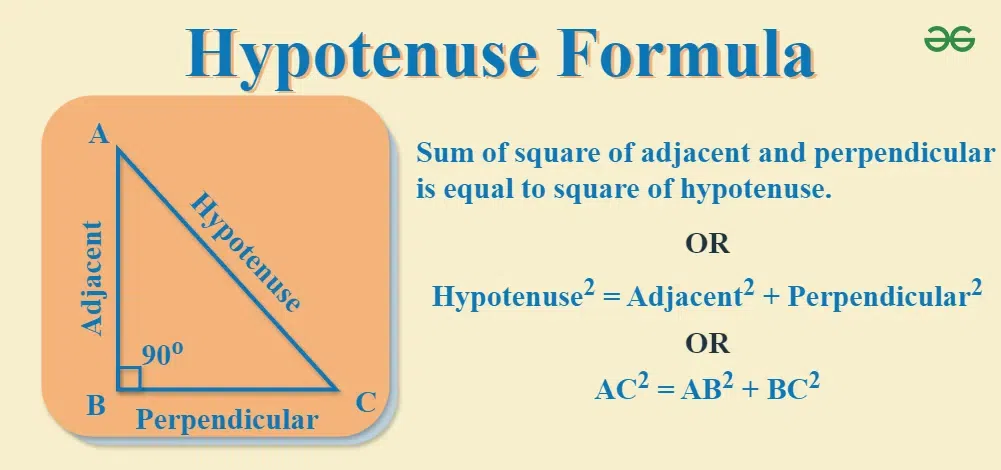
Hypotenuse Formula or Hypotenuse Theorem Formula is another name for Pythagoras Theorem. Hypotenuse Formula is used to calculate the third side of the right-angled triangle given the other two sides. Hypotenuse Formula can be defined as a relation among the three sides (hypotenuse, base, perpendicular) of a right-angled triangle. Hypotenuse Formula states that the sum of squares of two small sides(base and perpendicular) is equal to the square of the longest side (hypotenuse).

In this article, we will explore all the basic details of the Hypotenuse Formula, including the mathematical expression, proof, and various solved examples using the Hypotenuse Formula.

What is the Hypotenuse?

In a right angle triangle the one which is just one that falls opposite to 90 degrees is the Hypotenuse. The Hypotenuse is always the longest side of a right triangle. Furthermore, in a right triangle, the square of the length of the Hypotenuse is equal to the sum of the squares of the other two sides. The term hypotenuse occurred from the Ancient Greek word hypotenuse, which means ‘extending under a right angle’. The Hypotenuse will always be the longest side in a right triangle since it is opposite of the largest angle, the 90 degrees angle

Hypotenuse Formula in Triangle

By using Pythagoras Theorem Formula, we can calculate Hypotenuse Theorem Formula

Hypotenuse² = Perpendicular² + Base²

Here, c is denoting the length of the hypotenuse and a and b are denoting the lengths of the perpendicular and the base.

Pythagorean Theorem

Pythagorean theorem also known as Pythagoras’ theorem can be defined as a relation among the three sides (hypotenuse, base, perpendicular) of a right-angled triangle. It states that the sum of squares of two small sides(base and perpendicular) is equal to the square of the longest side (hypotenuse). This theorem is named after the Greek philosopher Pythagoras who was born around 570 BC.

Pythagoras theorem formula is c² = a² + b², where a is the perpendicular side, b is the base, and c is the hypotenuse side. The Pythagoras equation is applied to any triangle that has one of its angles equal to 90°.

Hypotenuse Formula Proof

As Pythagorean theorem shows the relation in the sides of a right-angled triangle, so if the length of any side is missing, it can be calculated using the Pythagorean Theorem.

In a right triangle ABC, right-angled at B.

To Prove: Hypotenuse² = Base² + Perpendicular²

In the below triangle ABC, let us draw a line from B to touch the side AC at angle D.

By similar triangles theorem, we can write the following equations such that,

△ADB ~ △ABC

So we can write equation as

⇒ AD/AB = AB/AC

⇒ AB²= AD × AC . . .(i)

Again, △BDC ~△ABC

So, we can write equation as follows

⇒ CD/BC = BC/AC

⇒ BC² = CD × AC . . .(ii)

Now, if we add (i) and (ii) we get;

AB² + BC² = (AD × AC) + (CD × AC)

Taking AC as common term from right side, we get;

⇒ AB² + BC² = AC × (AD + CD)

⇒ AB² + BC² = AC × (AC)

⇒ AB² + BC² = AC²

Hypotenuse² = Base²+ Perpendicular²

Hypotenuse = √ (Perpendicular²+ Base²)

Note: By using the lengths of both a (Perpendicular) and b (Base) , then the length of c (Hypotenuse) can be calculated:

The formula to calculate Hypotenuse:

Hypotenuse =√(Perpendicular²+ Base²)

OR

c = √(a² + b²)

Application of Hypotenuse Formula

There are many real-life application of Hypotenuse Theorem can be seen in day-to-day life and in various fields. Below are some of the applications:

• For Navigation, the Hypotenuse Theorem is calculated in order to find the shortest distance, etc.
• In order to recognize faces in security cameras, Hypotenuse Theorem is required to understand the distance of the person from the camera.
• In engineering fields, Hypotenuse Theorem is used to calculate the unknown dimension, say, the diameter of a particular sector.
• Hypotenuse is also used in electrical engineering.

How To Find Hypotenuse of a Right Angle Triangle

To find the Length of Hypotenuse in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to square root of the sum of the squares of the lengths of the other two sides.

The formula to find length of the hypotenuse is:

c = √(a² + b²)

Where:

c = the length of the hypotenuse.

a and b = the lengths of the other two sides of right angled triangle.

How To Find the Unknown Side of Right Triangle

To find the unknown side of right angled triangle:

If we need to find a, as a is the unknown side, then transform the hypotenuse equation to the form where a is on one side and take a square root:

Formula to find:

a = √(c² – b²)

If we need to find b, as b is the unknown side, then transform the equation to the form where a is on one side and take a square root:

Formula to find:

b = √(c² – a²)

For hypotenuse c is missing and we need to find c, the formula to calculate hypotenuse c side is:

Formula to find:

c = √(a² + b²)

Read More,

• Pythagorean Theorem Formula
• Right Angled Triangle

Hypotenuse Formula in Real-Life

Hypotenuse has many application in real life. We use hypotenuse formula in many situations like:

• We use hypotenuse formula in many calculations, like determine the heights of buildings, lengths of land boundaries.
• We use hypotenuse formula in construction or designing systems in engineering
• We use hypotenuse formula in navigation, which helps to calculate the distance between two locations.
• We use hypotenuse formula in electronics, which helps engineers to calculate the voltage and current in circuit.
• Pilots use hypotenuse formula to calculate the distance between two airports.
• We use hypotenuse formula in construction or designing the infrastructure of buildings.

Sample Problems on Hypotenuse Formula

Problem 1: Find the hypotenuse of a right angled triangle whose base is 6 cm and whose height is 8 cm?

Solution:

The formula to calculate Hypotenuse:

Hypotenuse =√ (Perpendicular²+ Base²)

c = √(a² + b²)

given ,base (a) =6,and perpendicular (b) =8

hence c = √(36 + 64)

c = √100

c = 10 cm.

Problem 2: Find the base of a right angled triangle whose hypotenuse is 13 cm and whose height is 12 cm?

Solution:

Using the formula to calculate Hypotenuse:

Hypotenuse =√ (Perpendicular²+ Base²)

c = √(a² + b²)

a(perpendicular)= 12, c(hypotenuse) = 13, find b(base)

So b = √(c2 – a2)

hence b = √(169 – 144)

b = √25 = 5 cm

Hence, the base of a right angled triangle =5 cm

Problem 3: Find the perpendicular of a right angled triangle whose hypotenuse is 25 cm and whose base is 7 cm?

Solution:

Using the formula to calculate Hypotenuse:

Hypotenuse =√ (Perpendicular²+ Base²)

c = √(a² + b²)

b(base)= 7, c(hypotenuse) = 25, find a(perpendicular)

so a = √(c2 – b2)

hence a = √(625 – 49)

a = √576

a = 24 cm.

Practice Problems on Hypotenuse Formula

Problem 1: Find the length of the Hypotenuse of a right triangle of which the other two sides measures 7 cm and 15cm?

Problem 2: Find the perpendicular of a right angled triangle whose hypotenuse is 30 cm and whose base is 7 cm?

Problem 3: The hypotenuse of a right angled triangle is 6 units. Its base is 2 units. Find its height using the hypotenuse formula?

Problem 4: Find the base of a right angled triangle whose hypotenuse is 15 cm and whose height is 12 cm?

Problem 5: Find the length of the Hypotenuse of a right triangle of which the other two sides measures 6 cm and 12cm?

Hypotenuse Formula: FAQs

What is the Pythagorean Theorem?

The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse c is equal to the sum of the squares of the lengths of the other two sides a and b:

c² = a² + b²

How is the Hypotenuse Formula used?

The formula is used to find the length of the hypotenuse when the lengths of the other two sides are known. This is particularly useful in geometry and trigonometry.

What are the Sides a, b, and c in the Hypotenuse Formula?

a and b are the legs of the right-angled triangle, and c is the hypotenuse. The right angle is always between a and b.

Can the Hypotenuse Formula be used for Non-Right-Angled Triangles?

No, the Pythagorean theorem is specifically applicable to right-angled triangles.

Can the Hypotenuse Formula be Rearranged to Solve for a or b?

Yes, the formula can be rearranged to solve for a or b. For example:

• Solving for a: a = √(c² – b²)
• Solving for b: b = √(c² – a²)

Are there Other Methods to find the Length of the Hypotenuse?

The hypotenuse formula is the most common method, but trigonometric ratios (sine, cosine, tangent) can also be used depending on the given information.

What units should be used for the sides and hypotenuse?

The units for the sides and hypotenuse should be consistent (e.g., all in meters, all in centimeters). It’s crucial to use the same units to ensure accurate calculations.

Can the Hypotenuse Formula be applied to any Unit of Measurement?

Yes, the formula is unit-agnostic, meaning it can be used with any unit of measurement as long as the units are consistent for all sides.

Can the Hypotenuse Formula be used for any Shape?

No, the hypotenuse formula is specific to right-angled triangles. Other shapes have their own methods for calculating side lengths or diagonals.