Horje
Find Edge Weights in a Spanning Tree with Edge (u, v)

Given an undirected weighted graph with N nodes and M edges, the task is for each edge (u, v) find the minimum possible weight of the Spanning Tree which contains the edge (u, v). The edges are given in the form of a 2D array edges[][], such that edges[i] = {u, v, w} denotes that there is a directed edge from node u to node v with weight w.

Examples:

Input: N = 5, M = 7, edges = {{1, 2, 3}, {1, 3, 1}, {1, 4, 5}, {2, 3, 2}, {2, 5, 3}, {3, 4, 2}, {4, 5, 4}}
Output: 9 8 11 8 8 8 9
Explanation:
tree

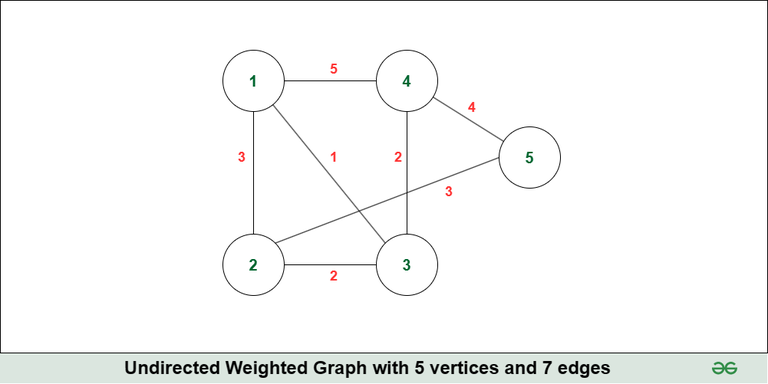
  • For edge (1, 2), the MST will have edges: (1, 2), (1, 3), (3, 4) and (2, 5), weight = 3 + 1 + 2 + 3 = 9
  • For edge (1, 3), the MST will have edges: (1, 3), (2, 3), (3, 4) and (2, 5), weight = 1 + 2 + 2 + 3 = 8
  • For edge (1, 4), the MST will have edges: (1, 3), (2, 3), (1, 4) and (2, 5), weight = 1 + 2 + 5 + 3 = 11
  • For edge (2, 3), the MST will have edges: (1, 3), (2, 3), (3, 4) and (2, 5), weight = 1 + 2 + 2 + 3 = 8
  • For edge (2, 5), the MST will have edges: (1, 3), (2, 3), (3, 4) and (2, 5), weight = 1 + 2 + 2 + 3 = 8
  • For edge (3, 4), the MST will have edges: (1, 3), (2, 3), (3, 4) and (2, 5), weight = 1 + 2+ 2 + 3 = 8
  • For edge (4, 5), the MST will have edges: (1, 3), (2, 3), (3, 4) and (4, 5), weight = 1 + 2 + 2 + 4 = 9

Input: N =2, M = 1, edges = {1, 2, 42}
Output: 42

Approach: The problem can be solved using the following approach:

We first build the Minimum Spanning Tree (MST) to ensure the overall minimum connection weight. Then, for all the edges which are in the MST, the answer will be the total weight of the MST. For edges which are not part of MST, say (u, v), we will remove the edge with maximum weight on the path from node u to node v and add edge (u, v).

To find the heaviest edge on the path from node u to node v, we find the heaviest edge from node u to node l and from node v to node l, where l is the Lowest Common Ancestor of node u and node v. We pre-compute ancestor and maximum weight information using Binary Lifting for efficient queries. This allows us to analyze individual edges by quickly finding the Lowest Common Ancestor (LCA) and adjusting the MST weight considering the maximum weight already covered, ultimately providing the minimum spanning tree weight with each edge included.

Steps to solve the problem:

  • Construct the MST using Kruskal’s Algorithm.
  • Preprocessing for Efficient Queries:
    • Perform a Depth First Search (DFS) starting from any node.
    • For each visited node, update the ancestor and maxWeight[] arrays at different levels for all its descendants.
    • Use Binary Lifting to calculate ancestor and maxWeight[] for each child node.
  • Processing Edge Queries:
    • For each edge, check if the edge is already included in the MST using the included array.
    • If the edge is included in the MST, the answer will be the weight of MST
    • Else, find the LCA of the edge endpoints and calculate the adjusted MST weight by adding the current edge’s weight and subtracting the maximum weight on the path to the LCA stored in the maxWeight[] array.
    • Print the adjusted MST weight.

Below is the implementation of the above approach:

C++

#include <bits/stdc++.h>
#define int long long
#define pii pair<int, int>
 
using namespace std;
const int N = 200005;
 
// Arrays to store ancestor, depth, and maxWeight
// information
int ancestor[N][50], depth[N], maxWeight[N][50];
 
// Arrays to store parent and subtreeSize for union-find
int parent[N], subtreeSize[N];
 
// Array to mark included edges in the minimum spanning tree
bool included[N];
 
// Adjacency list to represent the graph
vector<pii> adjacencyList[N];
 
// Function to find the Lowest Common Ancestor (LCA) and
// maximum weight on the path
int findLCA(int u, int v)
{
    int ans = -1;
    if (depth[u] != depth[v]) {
        if (depth[u] < depth[v])
            swap(u, v);
        int k = depth[u] - depth[v];
 
        // Iterate through binary representation of k
        for (int i = 0; (1 << i) <= k; i++)
            if ((k >> i) & 1) {
                ans = max(ans, maxWeight[u][i]);
                u = ancestor[u][i];
            }
    }
    if (u == v)
        return ans;
 
    // Find the LCA by moving up the tree in powers of 2
    int k = log2(depth[u]);
    for (int i = k; i >= 0; i--) {
        if (ancestor[u][i] != ancestor[v][i]) {
            ans = max(
                { maxWeight[u][i], maxWeight[v][i], ans });
            u = ancestor[u][i];
            v = ancestor[v][i];
        }
    }
    return max({ ans, maxWeight[u][0], maxWeight[v][0] });
}
 
// Depth-first search to construct ancestor and maxWeight
// arrays
void dfs(int u)
{
    for (auto x : adjacencyList[u]) {
        int v = x.first;
        int weight = x.second;
        if (v == ancestor[u][0])
            continue;
        ancestor[v][0] = u;
        maxWeight[v][0] = weight;
        depth[v] = depth[u] + 1;
 
        // Build ancestor and maxWeight arrays using dynamic
        // programming
        for (int j = 1; j <= 20; j++) {
            ancestor[v][j]
                = ancestor[ancestor[v][j - 1]][j - 1];
            maxWeight[v][j]
                = max(maxWeight[ancestor[v][j - 1]][j - 1],
                      maxWeight[v][j - 1]);
        }
        dfs(v);
    }
}
 
// Function to find the parent of a node using path
// compression
int findParent(int u)
{
    if (u == parent[u])
        return u;
    return parent[u] = findParent(parent[u]);
}
 
// Function to join two sets using union by size
void unionSets(int u, int v)
{
    u = findParent(u);
    v = findParent(v);
    if (subtreeSize[u] < subtreeSize[v])
        swap(u, v);
    subtreeSize[u] += subtreeSize[v];
    parent[v] = u;
}
 
signed main()
{
    // Static input
    int n = 5, m = 7;
    vector<pair<pii, pii> > edges, queries;
    vector<int> weightList = { 3, 1, 5, 2, 3, 2, 4 };
    vector<int> uList = { 1, 1, 1, 2, 2, 3, 4 };
    vector<int> vList = { 2, 3, 4, 3, 5, 4, 5 };
 
    // Input the edges
    for (int i = 1; i <= m; i++) {
        int u = uList[i - 1], v = vList[i - 1],
            weight = weightList[i - 1];
        queries.push_back({ { weight, i }, { u, v } });
        edges.push_back({ { weight, i }, { u, v } });
    }
 
    // Sorting edges based on weights
    sort(edges.begin(), edges.end());
 
    // Variable to store the total weight of the minimum
    // spanning tree
    int totalWeight = 0;
 
    // Initialize parent and subtreeSize arrays for
    // union-find
    for (int i = 1; i <= n; i++) {
        parent[i] = i;
        subtreeSize[i] = 1;
    }
 
    // Construct the minimum spanning tree
    for (auto x : edges) {
        int weight = x.first.first;
        int u = x.second.first;
        int v = x.second.second;
        int parentU = findParent(u);
        int parentV = findParent(v);
        if (parentU == parentV)
            continue;
        totalWeight += weight;
        included[x.first.second] = true;
        unionSets(u, v);
        adjacencyList[u].push_back({ v, weight });
        adjacencyList[v].push_back({ u, weight });
    }
 
    // Depth-first search to construct ancestor and
    // maxWeight arrays
    dfs(1);
 
    // Process each query
    for (auto x : queries) {
        int weight = x.first.first;
        int u = x.second.first;
        int v = x.second.second;
 
        // Check if the edge is already included in the
        // minimum spanning tree
        if (included[x.first.second]) {
            cout << totalWeight << ' ';
            continue;
        }
 
        // Find the weight of the Lowest Common Ancestor
        // (LCA)
        int lcaWeight = findLCA(u, v);
 
        // Output the minimum spanning tree weight with the
        // current edge
        cout << totalWeight - lcaWeight + weight << ' ';
    }
}

Java

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
 
class Edge implements Comparable<Edge> {
    int weight, id, u, v;
 
    Edge(int weight, int id, int u, int v)
    {
        this.weight = weight;
        this.id = id;
        this.u = u;
        this.v = v;
    }
 
    // Compare edges based on weights
    public int compareTo(Edge other)
    {
        return Integer.compare(this.weight, other.weight);
    }
}
 
public class Main {
 
    static int[][] ancestor = new int[200005][50];
    static int[] depth = new int[200005];
    static int[][] maxWeight = new int[200005][50];
    static int[] parent = new int[200005];
    static int[] subtreeSize = new int[200005];
    static boolean[] included = new boolean[200005];
    static ArrayList<int[]>[] adjacencyList
        = new ArrayList[200005];
    static ArrayList<Edge> edges = new ArrayList<>();
    static ArrayList<Edge> queries = new ArrayList<>();
 
    static
    {
        for (int i = 0; i < 200005; i++) {
            adjacencyList[i] = new ArrayList<>();
        }
    }
 
    // Function to find the Lowest Common Ancestor (LCA) and
    // maximum weight on the path
    static int findLCA(int u, int v)
    {
        int ans = -1;
        if (depth[u] != depth[v]) {
            if (depth[u] < depth[v]) {
                int temp = u;
                u = v;
                v = temp;
            }
            int k = depth[u] - depth[v];
 
            // Iterate through binary representation of k
            for (int i = 0; (1 << i) <= k; i++) {
                if ((k >> i & 1) == 1) {
                    ans = Math.max(ans, maxWeight[u][i]);
                    u = ancestor[u][i];
                }
            }
        }
        if (u == v)
            return ans;
 
        // Find the LCA by moving up the tree in powers of 2
        int k = (int)(Math.log(depth[u]) / Math.log(2));
        for (int i = k; i >= 0; i--) {
            if (ancestor[u][i] != ancestor[v][i]) {
                ans = Math.max(Math.max(maxWeight[u][i],
                                        maxWeight[v][i]),
                               ans);
                u = ancestor[u][i];
                v = ancestor[v][i];
            }
        }
        return Math.max(Math.max(ans, maxWeight[u][0]),
                        maxWeight[v][0]);
    }
 
    // Depth-first search to construct ancestor and
    // maxWeight arrays
    static void dfs(int u)
    {
        for (int[] x : adjacencyList[u]) {
            int v = x[0];
            int weight = x[1];
            if (v == ancestor[u][0])
                continue;
            ancestor[v][0] = u;
            maxWeight[v][0] = weight;
            depth[v] = depth[u] + 1;
 
            // Build ancestor and maxWeight arrays using
            // dynamic programming
            for (int j = 1; j <= 20; j++) {
                ancestor[v][j]
                    = ancestor[ancestor[v][j - 1]][j - 1];
                maxWeight[v][j] = Math.max(
                    maxWeight[ancestor[v][j - 1]][j - 1],
                    maxWeight[v][j - 1]);
            }
            dfs(v);
        }
    }
 
    // Function to find the parent of a node using path
    // compression
    static int findParent(int u)
    {
        if (u == parent[u])
            return u;
        return parent[u] = findParent(parent[u]);
    }
 
    // Function to join two sets using union by size
    static void unionSets(int u, int v)
    {
        u = findParent(u);
        v = findParent(v);
        if (subtreeSize[u] < subtreeSize[v]) {
            int temp = u;
            u = v;
            v = temp;
        }
        subtreeSize[u] += subtreeSize[v];
        parent[v] = u;
    }
 
    public static void main(String[] args)
    {
        int n = 5, m = 7;
        int[] weightList = { 3, 1, 5, 2, 3, 2, 4 };
        int[] uList = { 1, 1, 1, 2, 2, 3, 4 };
        int[] vList = { 2, 3, 4, 3, 5, 4, 5 };
 
        // Input the edges
        for (int i = 1; i <= m; i++) {
            int u = uList[i - 1], v = vList[i - 1],
                weight = weightList[i - 1];
            queries.add(new Edge(weight, i, u, v));
            edges.add(new Edge(weight, i, u, v));
        }
 
        // Sorting edges based on weights
        Collections.sort(edges);
 
        // Variable to store the total weight of the minimum
        // spanning tree
        int totalWeight = 0;
 
        // Initialize parent and subtreeSize arrays for
        // union-find
        for (int i = 1; i <= n; i++) {
            parent[i] = i;
            subtreeSize[i] = 1;
        }
 
        // Construct the minimum spanning tree
        for (Edge x : edges) {
            int weight = x.weight;
            int u = x.u;
            int v = x.v;
            int parentU = findParent(u);
            int parentV = findParent(v);
            if (parentU == parentV)
                continue;
            totalWeight += weight;
            included[x.id] = true;
            unionSets(u, v);
            adjacencyList[u].add(new int[] { v, weight });
            adjacencyList[v].add(new int[] { u, weight });
        }
 
        // Depth-first search to construct ancestor and
        // maxWeight arrays
        dfs(1);
 
        // Process each query
        for (Edge x : queries) {
            int weight = x.weight;
            int u = x.u;
            int v = x.v;
 
            // Check if the edge is already included in the
            // minimum spanning tree
            if (included[x.id]) {
                System.out.print(totalWeight + " ");
                continue;
            }
 
            // Find the weight of the Lowest Common Ancestor
            // (LCA)
            int lcaWeight = findLCA(u, v);
 
            // Output the minimum spanning tree weight with
            // the current edge
            System.out.print(totalWeight - lcaWeight
                             + weight + " ");
        }
    }
}

Python3

import math
from collections import defaultdict
 
N = 200005
 
# Arrays to store ancestor, depth, and maxWeight information
ancestor = [[0]*50 for _ in range(N)]
depth = [0]*N
maxWeight = [[0]*50 for _ in range(N)]
 
# Arrays to store parent and subtreeSize for union-find
parent = [0]*N
subtreeSize = [0]*N
 
# Array to mark included edges in the minimum spanning tree
included = [False]*N
 
# Adjacency list to represent the graph
adjacencyList = defaultdict(list)
 
# Function to find the Lowest Common Ancestor (LCA) and
# maximum weight on the path
def findLCA(u, v):
    ans = -1
    if depth[u] != depth[v]:
        if depth[u] < depth[v]:
            u, v = v, u
        k = depth[u] - depth[v]
 
        # Iterate through binary representation of k
        for i in range(int(math.log2(k))+1):
            if ((k >> i) & 1):
                ans = max(ans, maxWeight[u][i])
                u = ancestor[u][i]
    if u == v:
        return ans
 
    # Find the LCA by moving up the tree in powers of 2
    k = int(math.log2(depth[u]))
    for i in range(k, -1, -1):
        if ancestor[u][i] != ancestor[v][i]:
            ans = max(maxWeight[u][i], maxWeight[v][i], ans)
            u = ancestor[u][i]
            v = ancestor[v][i]
    return max(ans, maxWeight[u][0], maxWeight[v][0])
 
# Depth-first search to construct ancestor and maxWeight
# arrays
def dfs(u):
    for x in adjacencyList[u]:
        v, weight = x
        if v == ancestor[u][0]:
            continue
        ancestor[v][0] = u
        maxWeight[v][0] = weight
        depth[v] = depth[u] + 1
 
        # Build ancestor and maxWeight arrays using dynamic
        # programming
        for j in range(1, 21):
            ancestor[v][j] = ancestor[ancestor[v][j - 1]][j - 1]
            maxWeight[v][j] = max(maxWeight[ancestor[v][j - 1]][j - 1], maxWeight[v][j - 1])
        dfs(v)
 
# Function to find the parent of a node using path
# compression
def findParent(u):
    if u == parent[u]:
        return u
    parent[u] = findParent(parent[u])
    return parent[u]
 
# Function to join two sets using union by size
def unionSets(u, v):
    u = findParent(u)
    v = findParent(v)
    if subtreeSize[u] < subtreeSize[v]:
        u, v = v, u
    subtreeSize[u] += subtreeSize[v]
    parent[v] = u
 
def main():
    # Static input
    n = 5
    m = 7
    edges = []
    queries = []
    weightList = [3, 1, 5, 2, 3, 2, 4]
    uList = [1, 1, 1, 2, 2, 3, 4]
    vList = [2, 3, 4, 3, 5, 4, 5]
 
    # Input the edges
    for i in range(1, m+1):
        u = uList[i - 1]
        v = vList[i - 1]
        weight = weightList[i - 1]
        queries.append(((weight, i), (u, v)))
        edges.append(((weight, i), (u, v)))
 
    # Sorting edges based on weights
    edges.sort()
 
    # Variable to store the total weight of the minimum
    # spanning tree
    totalWeight = 0
 
    # Initialize parent and subtreeSize arrays for
    # union-find
    for i in range(1, n+1):
        parent[i] = i
        subtreeSize[i] = 1
 
    # Construct the minimum spanning tree
    for x in edges:
        weight = x[0][0]
        u = x[1][0]
        v = x[1][1]
        parentU = findParent(u)
        parentV = findParent(v)
        if parentU == parentV:
            continue
        totalWeight += weight
        included[x[0][1]] = True
        unionSets(u, v)
        adjacencyList[u].append((v, weight))
        adjacencyList[v].append((u, weight))
 
    # Depth-first search to construct ancestor and
    # maxWeight arrays
    dfs(1)
 
    # Process each query
    for x in queries:
        weight = x[0][0]
        u = x[1][0]
        v = x[1][1]
 
        # Check if the edge is already included in the
        # minimum spanning tree
        if included[x[0][1]]:
            print(totalWeight, end=' ')
            continue
 
        # Find the weight of the Lowest Common Ancestor
        # (LCA)
        lcaWeight = findLCA(u, v)
 
        # Output the minimum spanning tree weight with the
        # current edge
        print(totalWeight - lcaWeight + weight, end=' ')
    print()
 
main()

C#

using System;
using System.Collections.Generic;
using System.Linq;
 
public class Edge : IComparable<Edge>
{
    public int weight, id, u, v;
 
    public Edge(int weight, int id, int u, int v)
    {
        this.weight = weight;
        this.id = id;
        this.u = u;
        this.v = v;
    }
 
    // Compare edges based on weights
    public int CompareTo(Edge other)
    {
        return this.weight.CompareTo(other.weight);
    }
}
 
public class MainClass
{
    static int[,] ancestor = new int[200005, 50];
    static int[] depth = new int[200005];
    static int[,] maxWeight = new int[200005, 50];
    static int[] parent = new int[200005];
    static int[] subtreeSize = new int[200005];
    static bool[] included = new bool[200005];
    static List<int[]>[] adjacencyList = new List<int[]>[200005];
    static List<Edge> edges = new List<Edge>();
    static List<Edge> queries = new List<Edge>();
 
    static MainClass()
    {
        for (int i = 0; i < 200005; i++)
        {
            adjacencyList[i] = new List<int[]>();
        }
    }
 
    // Function to find the Lowest Common Ancestor (LCA) and maximum weight on the path
    static int FindLCA(int u, int v)
    {
        int ans = -1;
        if (depth[u] != depth[v])
        {
            if (depth[u] < depth[v])
            {
                int temp = u;
                u = v;
                v = temp;
            }
            int k = depth[u] - depth[v];
            for (int i = 0; (1 << i) <= k; i++)
            {
                if ((k >> i & 1) == 1)
                {
                    ans = Math.Max(ans, maxWeight[u, i]);
                    u = ancestor[u, i];
                }
            }
        }
        if (u == v)
            return ans;
 
        int k2 = (int)(Math.Log(depth[u]) / Math.Log(2));
        for (int i = k2; i >= 0; i--)
        {
            if (ancestor[u, i] != ancestor[v, i])
            {
                ans = Math.Max(Math.Max(maxWeight[u, i], maxWeight[v, i]), ans);
                u = ancestor[u, i];
                v = ancestor[v, i];
            }
        }
        return Math.Max(Math.Max(ans, maxWeight[u, 0]), maxWeight[v, 0]);
    }
 
    // Depth-first search to construct ancestor and maxWeight arrays
    static void Dfs(int u)
    {
        foreach (var x in adjacencyList[u])
        {
            int v = x[0];
            int weight = x[1];
            if (v == ancestor[u, 0])
                continue;
            ancestor[v, 0] = u;
            maxWeight[v, 0] = weight;
            depth[v] = depth[u] + 1;
            for (int j = 1; j <= 20; j++)
            {
                ancestor[v, j] = ancestor[ancestor[v, j - 1], j - 1];
                maxWeight[v, j] = Math.Max(maxWeight[ancestor[v, j - 1], j - 1],
                                           maxWeight[v, j - 1]);
            }
            Dfs(v);
        }
    }
 
    // Function to find the parent of a node using path compression
    static int FindParent(int u)
    {
        if (u == parent[u])
            return u;
        return parent[u] = FindParent(parent[u]);
    }
 
    // Function to join two sets using union by size
    static void UnionSets(int u, int v)
    {
        u = FindParent(u);
        v = FindParent(v);
        if (subtreeSize[u] < subtreeSize[v])
        {
            int temp = u;
            u = v;
            v = temp;
        }
        subtreeSize[u] += subtreeSize[v];
        parent[v] = u;
    }
 
    public static void Main()
    {
        int n = 5, m = 7;
        int[] weightList = { 3, 1, 5, 2, 3, 2, 4 };
        int[] uList = { 1, 1, 1, 2, 2, 3, 4 };
        int[] vList = { 2, 3, 4, 3, 5, 4, 5 };
 
        for (int i = 1; i <= m; i++)
        {
            int u = uList[i - 1], v = vList[i - 1], weight = weightList[i - 1];
            queries.Add(new Edge(weight, i, u, v));
            edges.Add(new Edge(weight, i, u, v));
        }
 
        edges.Sort();
 
        int totalWeight = 0;
        for (int i = 1; i <= n; i++)
        {
            parent[i] = i;
            subtreeSize[i] = 1;
        }
 
        foreach (var x in edges)
        {
            int weight = x.weight, u = x.u, v = x.v;
            int parentU = FindParent(u);
            int parentV = FindParent(v);
            if (parentU == parentV)
                continue;
            totalWeight += weight;
            included[x.id] = true;
            UnionSets(u, v);
            adjacencyList[u].Add(new int[] { v, weight });
            adjacencyList[v].Add(new int[] { u, weight });
        }
 
        Dfs(1);
 
        foreach (var x in queries)
        {
            int weight = x.weight, u = x.u, v = x.v;
            if (included[x.id])
            {
                Console.Write(totalWeight + " ");
                continue;
            }
            int lcaWeight = FindLCA(u, v);
            Console.Write(totalWeight - lcaWeight + weight + " ");
        }
    }
}
 
// This code is contributed by shivamgupta310570

Javascript

const N = 200005;
 
let ancestor = new Array(N).fill(null).map(() => new Array(50).fill(0));
let depth = new Array(N).fill(0);
let maxWeight = new Array(N).fill(null).map(() => new Array(50).fill(0));
let parent = new Array(N).fill(0);
let subtreeSize = new Array(N).fill(0);
let included = new Array(N).fill(false);
let adjacencyList = new Array(N).fill(null).map(() => []);
 
function findLCA(u, v) {
    let ans = -1;
    if (depth[u] !== depth[v]) {
        if (depth[u] < depth[v]) [u, v] = [v, u];
        let k = depth[u] - depth[v];
 
        for (let i = 0; (1 << i) <= k; i++) {
            if ((k >> i) & 1) {
                ans = Math.max(ans, maxWeight[u][i]);
                u = ancestor[u][i];
            }
        }
    }
    if (u === v) return ans;
 
    let k = Math.log2(depth[u]);
    for (let i = k; i >= 0; i--) {
        if (ancestor[u][i] !== ancestor[v][i]) {
            ans = Math.max(ans, Math.max(maxWeight[u][i], maxWeight[v][i]));
            u = ancestor[u][i];
            v = ancestor[v][i];
        }
    }
    return Math.max(ans, Math.max(maxWeight[u][0], maxWeight[v][0]));
}
 
function dfs(u) {
    for (let x of adjacencyList[u]) {
        let v = x[0];
        let weight = x[1];
        if (v === ancestor[u][0]) continue;
        ancestor[v][0] = u;
        maxWeight[v][0] = weight;
        depth[v] = depth[u] + 1;
 
        for (let j = 1; j <= 20; j++) {
            ancestor[v][j] = ancestor[ancestor[v][j - 1]][j - 1];
            maxWeight[v][j] = Math.max(maxWeight[ancestor[v][j - 1]][j - 1], maxWeight[v][j - 1]);
        }
        dfs(v);
    }
}
 
function findParent(u) {
    if (u === parent[u]) return u;
    return parent[u] = findParent(parent[u]);
}
 
function unionSets(u, v) {
    u = findParent(u);
    v = findParent(v);
    if (subtreeSize[u] < subtreeSize[v]) [u, v] = [v, u];
    subtreeSize[u] += subtreeSize[v];
    parent[v] = u;
}
 
// Static input
let n = 5, m = 7;
let edges = [];
let queries = [];
let weightList = [3, 1, 5, 2, 3, 2, 4];
let uList = [1, 1, 1, 2, 2, 3, 4];
let vList = [2, 3, 4, 3, 5, 4, 5];
 
// Input the edges
for (let i = 1; i <= m; i++) {
    let u = uList[i - 1], v = vList[i - 1], weight = weightList[i - 1];
    queries.push([{ weight, index: i }, { u, v }]);
    edges.push([{ weight, index: i }, { u, v }]);
}
 
// Sorting edges based on weights
edges.sort((a, b) => a[0].weight - b[0].weight);
 
// Variable to store the total weight of the minimum spanning tree
let totalWeight = 0;
 
// Initialize parent and subtreeSize arrays for union-find
for (let i = 1; i <= n; i++) {
    parent[i] = i;
    subtreeSize[i] = 1;
}
 
// Construct the minimum spanning tree
for (let x of edges) {
    let weight = x[0].weight;
    let u = x[1].u;
    let v = x[1].v;
    let parentU = findParent(u);
    let parentV = findParent(v);
    if (parentU === parentV) continue;
    totalWeight += weight;
    included[x[0].index] = true;
    unionSets(u, v);
    adjacencyList[u].push([v, weight]);
    adjacencyList[v].push([u, weight]);
}
 
// Depth-first search to construct ancestor and maxWeight arrays
dfs(1);
 
// Process each query
for (let x of queries) {
    let weight = x[0].weight;
    let u = x[1].u;
    let v = x[1].v;
 
    if (included[x[0].index]) {
        process.stdout.write(totalWeight + ' ');
        continue;
    }
 
    let lcaWeight = findLCA(u, v);
    process.stdout.write((totalWeight - lcaWeight + weight) + ' ');
}

Output

9 8 11 8 8 8 9

Time Complexity: O(M log M + M log N), where N is the number of nodes and M is the number of edges.
Auxiliary Space: O(N log N + N + M)


 


Reffered: https://www.geeksforgeeks.org

Competitive Programming

Related
Find the Longest Non-Prefix-Suffix Substring in the Given String Find the Longest Non-Prefix-Suffix Substring in the Given String
Minimizing and Maximizing longest Increasing Subsequence (LIS) Minimizing and Maximizing longest Increasing Subsequence (LIS)
Sum and Update Queries on 3D Matrix in log(N) time Sum and Update Queries on 3D Matrix in log(N) time
Connecting Nodes in a Graph with Sum-based Edge Conditions Connecting Nodes in a Graph with Sum-based Edge Conditions
Heap Data Structure for Competitive Programming Heap Data Structure for Competitive Programming

Type:
 Geek
Category:
 Coding
Sub Category:
 Tutorial
Uploaded by:
 Admin
Views:
 16



 

Horje