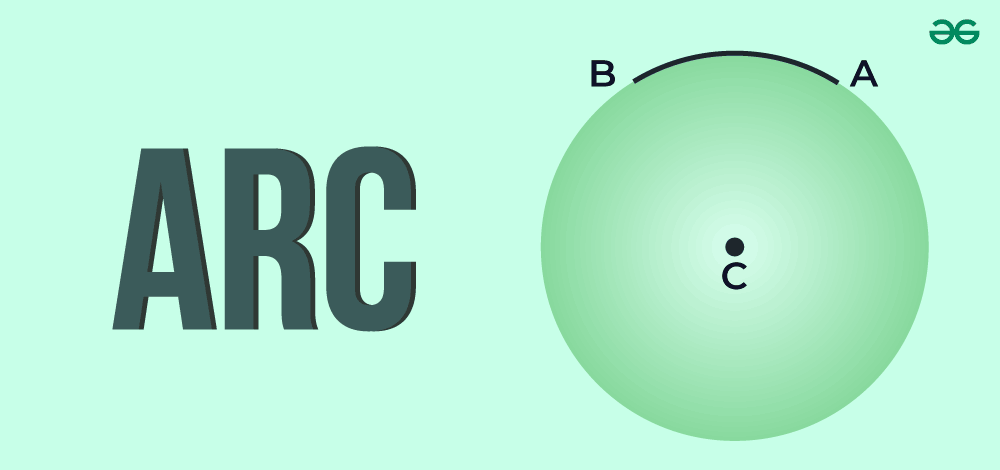
Arc is a segment of the circumference of a circle or any curved shape. An Arc in geometry is any smooth curve connecting two specific points. Arc is a smooth curve linking these endpoints. The length of an Arc is known as its Arc length. In Mathematics, it commonly refers to a portion of a circle, but it can also be parts of other shapes such as spheres, ellipses, and cylinders.

In this article, we will discuss the introduction, definition, types, and application of an Arc and its meaning. We will also understand measures and formulae to calculate the Arc Length and Arc Angle in mathematics. We will also solve various examples and provide practice questions for a better understanding of the concept of this article.

What is Arc in Math?

From the perspective mathematics, an Arc is a smooth curve connecting two distinct points at a certain distance. This curve can be a fragment of a circle, ellipse, or even a hyperbola. In specific cases, it is denoted as a segment of a circle, termed a circular arc. If we extend the ends of an arc, it will form a perfect circle.

Arc is also referred to as an ‘open curve.’ The circle’s perimeter, known as the circumference, defines the boundary. Thus, an arc measures the distance between two traced points along its circumference. For two arcs to be alike, their central angles must be equal.

Definition of Arc

An Arc is the part of a circle’s circumference that lies between two radii.

Arc represents a section of a curve, typically a circle, within a two-dimensional plane. Specifically, if the curve is a circle, we refer to it as a circular arc. In the strictest definition, an Arc is a segment of a curve located on a plane.

Symbol of Arc

The arc in geometry is typically represented by symbols ⌒ or ⌢ and is denoted as ‘arc AB,’ pronounced as such. Hence, ‘arc AB’ can be expressed as AB or equivalently as BA. The sequence of the points does not affect its order.

Arc of a Circle

A Circle is defined as the set of all points in a two-dimensional plane that maintains a constant distance from a fixed point in the same plane, known as the Center. This fixed distance between any point on the circle’s perimeter and the center is referred to as the radius. An Arc of a Circle represents a segment of its circumference.

Consider two random points, P and Q, situated on the circle’s surface. These points are connected to the Circle’s center, forming an angle. This angle, known as the angle subtended by the Arc at the Circle’s center, divides the circle into two distinct arcs: the Minor Arc PQ (‘P to Q’ in the counter-clockwise direction) and the Major Arc PQ (‘P to Q’ in the clockwise direction). The difference between these Arcs is reflected in their respective lengths and the angles they subtend at the circle’s center.

Types of Arcs

An Arc in a circle divides the circle into two distinct parts: a shorter segment known as the Minor Arc and a longer segment known as the Major Arc.

Minor Arc

The Minor Arc refers to an arc that will be less than half of the entire circumference of a circle. In the given circle, ∠PQ represents a Minor Arc. This shorter Arc connects two endpoints on the circle and is characterized by an angle (central angle) equal to its arc measure, which is less than 180°.

Major Arc

A Major Arc covers more than half of the circle’s circumference. In the given circle, ∠QP corresponds to the Major Arc. This longer Arc links two endpoints on the circle and has a measure exceeding 180°. The measure of a Major Arc is calculated as 360° minus the measure of the corresponding Minor Arc with the same endpoints.

Semicircle

An arc that measures exactly 180° is termed a Semicircle. A semicircle is basically half of a circle when a circle is bisected along its diameter.

Applications of an Arc

Arc has important role in construction and other designs. Let’s see some of the applications of Arc shape

• An arc is most widely used in the construction of bridges spanning streams and rivers of various sizes and designs.
• It is used in creating architectural elements such as arches over roofs and forming domes.
• Arcs in structures not only facilitate functionality but also enhance the overall visual of a building.
• The design of Arcs plays a important role in efficiently transmitting TV and radio signals via high-speed cables.
• The traditional bow used by archers showcases a prominent arc or curved shape, fundamental to its design and function.
• Whenever an object like a coin or stone is tossed into the air, the resulting path will follow a curved arc.

Central Angle or Angle of Arc

The Central Angle or Angle of the Arc is simply the angle that is formed at the center of the circle by the two radii that connect to the endpoints of the arc. A central angle is nothing but the angle that is subtended by the Major or Minor Arc at the center of any circle.

How to Make an Arc?

To form an Arc, you have two options: Use chord and a definite central angle.

• A chord is a straight line segment that connects two points anywhere on the circle’s circumference.
• Alternatively, a Central Angle is the angle created by two radii of the circle, taken from the center

We can also make an Arc of a circle using three point method. Let’s learn step of making arc of a circle using three point method.

Step 1: Assume three random points which are non collinear

Step 2: Draw two lines connecting these two points

Step 3: Draw Perpendicular bisectors of these two lines and extend them such that they intersect each other

Step 4: Assume the point of Intersection of Perpendicular Bisectors as Centre and extend the pencil to one the three points assuming the distance as radius

Step 5: Now draw the arc passing through the three Points

Measures of an Arc

There are two methods to measure an arc:

• Arc Angle: Measuring the angle formed by the Arc.
• Arc Length: Measuring the distance along the Arc.

Arc Length

Length of Arc is calculated in distance units like centimetres. To signify this measurement, we use the lowercase letter L (representing ‘length’) preceding the Arc.

Arc Length (L) = θ × r (when θ is in radians)

Arc Length (L) = θ × (π/180)× r (when θ is in degrees)

Angle of Arc

The Angle formed by an Arc at the center of the circle is the Angle of Arc. With the help of the Arc length formula, we can find the measure of Arc Angle.

θ = L/r

θ = {L × 180}/π × r

Arc Formula

In the preceding sections, we discussed the definition of an Arc and its categorization into Major and Minor Arcs. Now, let’s see various formulas associated with Arcs.

Formula for Arc Length

The Arc Length of a circle represents the distance between two endpoints along the Arc of a circle. The Arc Length is always greater than the straight-line distance between these endpoints. When the Arc’s ends are extended to the circle’s center through straight lines, an angle is formed. This angle is linked to the Arc Length (L).

Furthermore, the straight lines connecting the Arc’s endpoints to the circle’s center are the radii of the circle. The Arc Length can be expressed in terms of the circle’s radius and the angle subtended by the Arc at the circle’s center. Arc length is always measured in units of distance or length, such as millimeters (mm), centimeters (cm), meters (m), and so on.

When the Central Angle (θ) is measured in radians, the formula for Arc Length is given by:

L = θ × r

Where,

• L is the Arc’s Length.
• θ is the Central Angle of the Arc in radians.
• r is the radius of the circle.

Arc Length Formula for the angle in degrees:

Arc Length = θ × (180°/π) × r

OR

Arc Length = (360°/θ) × 2 × π × r

OR

Arc Length = (360°/θ) × π × d

Where,

• r is the radius of the circle.
• θ is the Central Angle of the arc in degrees.
• d is the diameter of the circle.

Note: 180°/π is the conversion factor from degrees to radians.

Arc Angle Formula

In the preceding section, we discussed the formulas for calculating Arc Length given the angle in either degrees or radians. Now, let’s focus on the formula for the angle subtended by the Arc at the center of a circle.

Arc Length = (360°/θ) × 2 × π × r

OR

Arc Length= (360°/θ) × C

Where C is the circumference of the circle, given by 2πr.

Hence, Arc Angle Formula

θ = (Arc Length × 360°)/C

Where, C is the circumference of the Circle

Note: This formula calculates the angle in degrees. To obtain the angle in radians, you can multiply the angle measure in degrees by π/ 180°

Radius of a Circle from Width and Height of Arc

If we are given the width and height of aarc then we can calculate the Radius of a Circle using the formula given below:

Radius = {height²+(width/2)²}/2 × height

Summary

All the formulas discussed in the article are summarized in the following table: