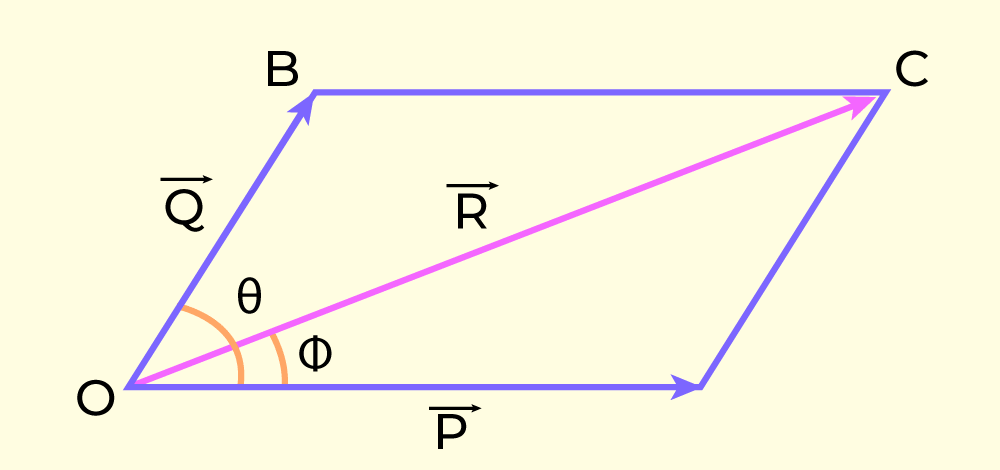
Parallelogram Law of Vector Addition explains that when two vectors are considered to be the two adjacent sides of a parallelogram with their tails meeting at the common point, then the diagonal of the parallelogram originating from the common point will be the resultant vector. It is also known as Parallelogram Law in Vector Algebra.

Parallelogram Law of Vector Addition is basically the mathematical expression for vector addition. This law is used to add two vectors when the vectors form two adjacent sides of the parallelogram formed by combining the tails of these two vectors to produce or make the parallelogram itself then the diagonal of the parallelogram is used to calculate the sum of the two vectors which is called resultant vector.

Here, in this article we will learn in detail, the Parallelogram Law of Vector Addition along with a brief introduction to vector addition. We will also learn Parallelogram Law of Vector Addition Formula, Derivation of Parallelogram Law of Vector Addition Formula, its different cases, and its application.

What is Vector Addition

Vector Addition is a mathematical operation that combines two or more vectors to produce a new vector called Resultant Vector. While we can simply add any two scalar quantities but while adding the two vectors we need to be careful about their direction which are given by their unit vectors.

Vector Addition is very useful and important method in Mathematics and Physics for analyzing and solving problems involving forces, velocities, displacements, and many other physical quantities. It is also applicable for the combination of multiple forces, velocities, or displacements to determine their net effect or resultant.

What is Parallelogram Law of Vector Addition?

The Parallelogram Law of Vector Addition is a fundamental principle in vector mathematics that explains how to add two vectors. It describe that when two vectors are added together, their sum is represented by the diagonal of the parallelogram that starts from the same point as the two vectors which is called resultant vector.

Parallelogram Law of Vector Addition Definition

Parallelogram Law of Vector Addition states when two vectors are added together and their sum is represented by the diagonal of the parallelogram. It is a mathematical principle that tells about how to add two vectors geometrically to find their resultant vector.

Parallelogram Law of Vector Addition Formula

In Parallelogram Law of Vector Addition Formula we will learn the formula to find the magnitude of Resultant Vectors and Formula to find the direction of Resultant Vector.

Formula for Magnitude of Resultant Vector R

|R| = √(P² + Q² + 2PQcosθ)

Where,

• A and B are the magnitudes (lengths) of vectors P and Q, respectively.
• θ is the angle between vectors P and Q.

In these formulas, P² and Q² represent the squares of the magnitudes of vectors P and Q, and cosθ is the cosine of the angle between the vectors.

Formula for Direction of Resultant Vector R

Let the Resultant Vector R make Φ angle with vector P then the direction of resultant vector is given as follows

tan ϕ = [( Qsinθ ) / (P + Qcosθ )]

Derivation of Parallelogram Law of Vector Addition

Consider two vectors, P and Q respectively represented by arrows with directions and magnitudes.

Let θ be the angle between P and Q and R be the resultant vector. Then according to Parallelogram Law of Vector Addition, diagonal OC represent the resultant vector of P and Q.

So we have,

R = P + Q

Now expand A to D and draw a perpendicular CD to OD.

From triangle ODC,

(OC)²= (OD)² + (CD)² [By Pythagoras theorem]

⇒ (OC)²= (OA + AD)² + (CD)² . . . (1)

In triangle ADC

Cosθ = AD/AC or AD = AC Cosθ or AD = OB Cosθ = Q Cosθ

Also,

Sinθ = CD/AC or CD = AC Sinθ or CD = OB Sinθ = Q Sinθ

Magnitude of resultant-

Substituting the value of AD and CD in equation-1

(OC)²= (OA + AD)² + (CD)²

⇒ (R)² = (P + QCosθ)² + (QSinθ)²

⇒ R² = P² + 2PQCosθ + Q²Cos² + Q²Sinθ²

⇒ |R| = √(P² + Q² + 2PQCOsθ)

Hence, Proved.

Cases for Parallelogram Law of Vector Addition

There are some cases where the Parallelogram Law of Vector Addition can be applied: When

Vectors are Parallel (θ = 0°)

When two vectors are parallel and have the same direction, the law simplifies to simple addition then the resultant vector will have the same direction as the original vectors and a magnitude equal to the sum of their magnitudes.

|R| = √(P²+ Q²+ 2PQcosθ)

Since, θ = 0°

⇒ |R| = √(P² + Q²+ 2PQcos0)

⇒ |R| = √(P² + Q²+ 2PQ)

⇒ |R| = √(P + Q)²

⇒ |R| = P + Q

When two vectors are in the same direction, the resultant vector is their algebraic sum given by using R = P + Q where R is the resultant vector, P and Q are the parallel vectors.

Vectors are in Opposite Direction (θ = 180°)

When two vectors are in opposite directions, the resultant vector will have a magnitude of zero because the vectors cancel each other out.

|R| = √(P²+ Q²+ 2PQcosθ)

Since, θ = 180°

|R| = √(P²+ Q²+ 2PQcos180)

⇒ |R| = √(P²+ Q²– 2PQ)

⇒ |R| = √(P – Q)²

⇒ |R| = P – Q

By using parallelogram law of vector addition R = P – Q, where R is the resultant vector, P is the first vector, and Q is the second vector. When the vectors are in opposite directions, the value of θ = 180 degree.

Vectors are Perpendicular (θ = 90°)

When two vectors are perpendicular to each other, by using the Pythagorean theorem, we can find magnitude of the resultant vector is equal to the square root of the sum of the squares of the magnitudes of the two vectors.

|R| = √(P²+ Q²+ 2PQcosθ)

Since, θ = 90°

⇒ |R| = √(P²+ Q²+ 2PQcos90)

⇒ |R| = √(P²+ Q²– 0)

⇒ |R| = √(P² + Q²)

When vectors are perpendicular, their angles (θ) between them are typically 90 degrees. Using the Parallelogram Law of Vector Addition R = √(P² + Q² + 2PQcosθ) since (θ = 90 degree) so, the formula is R = √(P² + Q²).

Application of Parallelogram Law of Vector Addition

The various applications of Parallelogram Law of Vector Addition is listed below:

• In physics, this law is used to calculate the resultant of two forces acting at an angle to each other.
• It is applied in navigation and aviation to determine the resultant velocity or displacement when an object has both horizontal and vertical components of motion.
• It is crucial for flight planning and navigation.
• It helps calculate the resultant motion or direction of an object when multiple forces or transformations are applied simultaneously.
• It helps the students to find the resultant of two vectors very easily.
• Astronomers use parallelogram law of vector addition to analyze the motion of celestial bodies like planets and stars. It also helps to determine its resulting path or orbit when multiple gravitational forces are acting on an object.

Must Read

• Triangle law of vector
• Dot and Cross Product of Vector
  
• Magnitude of Vectors

Solve Examples on Parallelogram Law of Vector Addition

Example 1: Two forces of 6 N and 8 N are acting at a point such that the angle between them is 60 degrees. Find the resultant force.

Solution:

Magnitude R of the resultant force is given by:

[(6)² + (8)² + 2 x 6 x 8 Cos 60°}

√(36 + 64 + 48) = √(148 = 12.16 N

Hence, the magnitude R of the resultant force is 12.16 N.

Example 2: A truck goes 6 km east 3 km south, 2 km west and 1 km north. Find the resultant displacement.

Solution:

O to A 6 km East

A to B 3 km South

B to C 2 km West

C to D 1 km North

Net displacement = OD

Along the horizontal direction: 6 km East – 2 km West = 4 km East

Along the vertical direction: 3 km south – 1 km north = 2 km South

⇒ OD = √(4² + 2² + 2 x 3 x 4 x Cos 90 deg)

⇒ OD = √(4²+ 2²⁾

⇒ OD = 4.47 Km

⇒ Tan p = 2/3

p = 34°

Hence, the resultant displacement is 4.47 km, 34° South of East.

Example 3: If we have two forces 10 N and 20 N are acting at an angle of 120° between them, then for calculating the resultant we do the following.

Solution:

Let one force be A and other force be B and θ be the angle between A and B.

A = 10N, B = 20N, θ = 120°

⇒ |R| = √[(A)² + (B)² + 2 x A x B Cos 120°]

⇒ |R| = √[(10)²+ (20)² + 2 x 10 x 20 Cos 120°]

⇒ |R| = √[100 + 400 + 200]

⇒ |R| = √700 = 26.45

Hence, the required resultant is 26.45N.

Example 4: Given two vectors 10i − 3j + k and 20 i − 8 j + 20 k which are parallel, find the resultant vector for them.

Solution:

Let, A vector = 10i − 3j + k and B vector = 20i − 8j + 20k

We know that if two vectors are parallel, then the angle between them is zero and the resultant is just the sum of given vectors.

R vector = A vector + B vector [θ=0]

So,

= (10i − 3j + k) + (20i – 8j + 20k)

= 30i − 11j + 21k

Hence, R is the resultant addition for the two given vectors in the same direction.

Practice Questions on Parallelogram Law of Vector Addition

Q1. If two vectors A and B have magnitudes of 6 units and 8 units, respectively. The angle between them is 120 degrees. Find the magnitude and direction of their resultant vector using the Parallelogram Law of Vector Addition.

Q2. Vector R1 has a magnitude of 10 units, directed at an angle of 60 degrees above the x-axis. Vector V2 has a magnitude of 15 units, directed at an angle of 30 degrees above the x-axis. Find the resultant vector R using the Parallelogram Law.

Q3. There are two vector of magnitudes 10 and 20 units, and the angle between then is 120 degree. Calculate the direction and the magnitude of their resultant vector using the Parallelogram Law of vector addition.

Q4. If you have two vectors V1 and V2 of magnitudes 15 N and 20 N, respectively. If the angle between them is 120 degrees then calculate the direction and the magnitude of the resultant force using the Parallelogram Law of Vector Addition.

Q5. State and Prove Parallelogram Law of Vector Addition.

Parallelogram Law of Vector Addition – FAQs

What is Parallelogram Law of Vector Addition?

Parallelogram Law of Vector Addition, also famously known as the “Parallelogram Identity. It states or explains that when two vectors are considered to be the two adjacent sides of a parallelogram with their tails meeting at the common point, then the diagonal of parallelogram originating from the common point will be the resultant vector.

Who discovered the Parallelogram Law of Vector Addition?

Vector mathematics was developed in the 19th century by mathematicians like Josiah Willard Gibbs and Oliver Heaviside, who established the formal framework for working with vectors, including vector addition, in a more systematic way. It is a geometric concept, it has been known for centuries and is not attributed to a single individual. Instead, it is a fundamental principle in vector mathematics and geometry. It is a geometric intuition that has been used by mathematicians, scientists, and engineers for a long time.

What are application of the Parallelogram Law of Vector Addition?

The applications of Parallelogram Law of Vector Addition are listed below

• Mechanics and Kinematics
• Electromagnetism
• Navigation and Aviation
• Engineering
• Computer Graphics

What is the Formula of Parallelogram Law of Vector Addition?

The formula for the Parallelogram Law of Vector Addition is |R| = √(P² + Q² + 2PQ.Cosθ). This formula states that to find the resultant vector when adding two vectors together, you add them component-wise. In other words, you add the corresponding components of vector P to the corresponding components of vector Q to get the components of the resultant vector R.

Can we use the Parallelogram Law of vector addition for subtracting vectors as well?

Yes, we can use the Parallelogram Law of vector addition for subtracting vectors. To subtract one vector from another, we simply reverse the direction of the vector you want to subtract and then apply the law to find the resultant vector.

Is there any mathematical formula for the Parallelogram Law of vector addition?

Yes, there is a mathematical formula that represents the Parallelogram Law: R vector = A vector + B vector , where R vector is the resultant vector, and A vector and B vector are the two vectors being added.

What is Parallelogram Law of Forces?

It is also known as ‘Parallelogram Law of Vector Addition’ and it defines that when two forces act on an object, represented as vectors, are applied to a point simultaneously, then the resultant force can be determined by constructing a parallelogram. In other words, It is used find the resultant (net) force when two forces act on an object in physics and engineering.