Local Maxima and Minima refer to the points of the functions, that define the highest and lowest range of that function. The derivative of the function can be used to calculate the Local Maxima and Local Minima. The Local Maxima and Minima can be found through the use of both the First derivative test and the Second derivative test.

In this article, we will discuss the introduction, definition, and important terminology of Local Maxima and Minima and its meaning. We will also understand the different methods to calculate the Local Maxima and Minima in mathematics and calculus. We will also solve various examples and provide practice questions for a better understanding of the concept of this article.

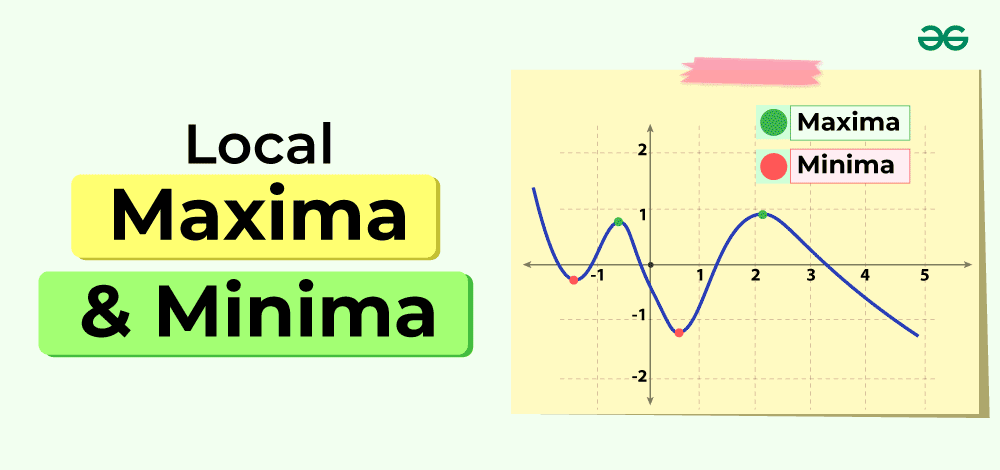
What is Local Maxima and Local Minima?

Local Maxima and Minima are referred to as maximum and minimum values in a specific interval. A Local Maximum occurs when the values of a function near a specific point are always lower than the values of the function at the same point. In the case of Local Minima, the values of a function near a specific point are always greater than the values of the function at the same point.

In a simple sense, a point is called a Local maximum when the function reaches its highest value in a specific interval, and a point is called a Local minimum when the function reaches its lowest value in a specific interval.

For example, if you go to a hilly area and stand on the peak of a hill, that point is called a Local Maxima point because you are at the highest point in your surroundings. Similarly, If you are standing at the lowest point in a river or sea that point is called a Local Minima point because you are at the lowest point in your surroundings.

Definition of Local Maxima and Local Minima

Local Maxima and Minima are the initial values of any function to get an idea about its boundaries such as the highest and lowest output values. Local Minima and Local Maxima are also called Local Extrema.

Local Maxima

A Local Maxima point is a point on any function where the function attains its maximum value within a certain inteval. A point (x = a) of a function f (a) is called a Local maximum if the value of f(a) is greater than or equal to all the values of f(x).

Mathematically, f (a) ≥ f (a -h) and f (a) ≥ f (a + h) where h > 0, then a is called the Local maximum point.

Local Minima

A Local Minima point is a point on any function where the function attains its minimum value within a certain interval. A point (x = a) of a function f (a) is called a Local minimum if the value of f(a) is lesser than or equal to all the values of f(x).

Mathematically, f (a) ≤ f (a -h) and f (a) ≤ f (a + h) where h > 0, then a is called the Local minimum point.

Terms Related to Local Maxima and Local Minima

Important terminology related to Local Maxima and Minima are discussed below:

Maximum Value

If any function gives the maximum output value for the input value of x. That value of x is called maximum value. If it is defined within a specific range. Then that point is called Local Maxima.

Absolute Maximum

If any function gives the maximum output value for the input value of x along the entire range of the function. That value of x is called Absolute Maximum.

Minimum Value

If any function gives the minimum output value for the input value of x. That value of x is called minimum value. If it is defined within a specific range. Then that point is called Local Minima.

Absolute Minimum

If any function gives the minimum output value for the input value of x along the entire range of the function. That value of x is called Absolute Minimum.

Point of Inversion

If the value of x within the range of given function does not show the highest and lowest output, is called the Point of Inversion.

Read More, Absolute Maxima and Minima

How to Find Local Maxima and Minima?

The Local Maxima and the Minima are determined for only specific range, it is not the maximum and minimum for the entire function and do not apply to the entire range of the function.

There are following approach to calculate the Local Maxima and Minima. These are:

• In first step, we take the derivative of function.

• In second step, we set the derivative equal to zero and calculate the critical points for c.

• In third step, we use First derivative and Second derivative test to determine the Local Maxima and Local Minima.

What is First Derivative Test?

Firstly, we take the First derivative of a function which gives the slope of the function. As we get closer to a maximum point, the slope of the function increases, then becomes zero at the maximum point, and after that decreases as we go away from it.

Similarly in the minimum point, as we get closer to a minimum point, the slope of the curve decreases, then becomes zero at the minimum point, and after that increases as we go away from that point.

Let us take a function f(x), which is continuous at the critical point c, in an open interval I, and f'(c) = 0, means slope at critical point c = 0.

To check the nature of f'(x) around the critical point c, we have the following conditions to determine the value of Local maximum and minimum from the First derivative test. These conditions are:

• If f ′(x) changes sign from positive to negative as x increases via c, then f(c) shows the highest value of that function in the given range. Hence, point c is a Local Maxima point, if the first derivative f ‘(x) > 0 at any point enough close to the left of c and f ‘(x) < 0 at any point enough close to the right of c.

• If f ′(x) changes sign from negative to positive as x increases via c, then f(c) shows the lowest value of that function in the given range. Hence, point c is a Local Minima point, if the first derivative f ‘(x) < 0 at any point enough close to the left of c and f ‘(x) > 0 at any point enough close to the right of c.

• If f'(x) doesn’t change the sign significantly with x increasing via c, then the point c does not show the highest (Local Maxima) and lowest (Local Minima) value of the function, In such case, point c is called Point of Inflection.

Read more about First Derivative Test.

What is Second Derivative Test?

The Second derivative test is used to find out the value of absolute maximum and absolute minimum of any function within specific interval. Let us take a function f(x), which is continuous at the critical point c, in an open interval I, and f'(c) = 0, means slope at critical point c = 0. Here we take the second derivative f”(x) of the function f(x) which gives the slope of the function.

To check the nature of f'(x), we have the following conditions to determine the value of Local maximum and minimum from the Second derivative test. These conditions are:

• Point c is a Local Maxima point, if the first derivative f'(c) = 0, and the second derivative f”(c) < 0. The point at x= c will be the Local Maxima and f(c) will be the Local maximum value of f(x).

• Point c is a Local Minima point, if the first derivative f'(c) = 0, and f”(c) the second derivative > 0. The point at x= c will be the Local Minima and f(c) will be the Local minimum value of f(x).

• The test fails, if the first derivative f'(c) = 0, and the second derivative f”(c) = 0, then the point c does not show the highest (Local Maxima) and lowest (Local Minima) value of the function, In such case, point c is called Point of Inflection and the point x = c is called the Point of Inflection.

Also, Check

• Application of Derivatives
• Relative Maxima and Minima
• Differentiation & Integration Formula

Properties of Local Maxima and Minima

Understanding the properties of local maxima and minima can help in their identification:

1. If a function f(x) is continuous in its domain, it must have at least one maximum or minimum between any two points where the function values are equal.
2. Local maxima and minima occur alternately; between two minima, there must be a maximum, and vice versa.
3. If f(x) approaches infinity as x approaches the endpoints of the interval and has only one critical point within the interval, that critical point is an extremum.

Critical Points and Their Significance

Critical points are where the first derivative of a function is zero or undefined. These points are significant as they potentially indicate locations of local maxima, minima, or saddle points (inflection points where the function changes curvature but not necessarily reaching an extremum).

Solved Examples on Local Maxima and Local Minima

Example 1: Analyze the Local Maxima and Local Minima of the function f(x) = 2x³ – 3x² – 12x + 5 by using the first derivative test.

Solution:

Given function is f(x) = 2x³ – 3x² – 12x + 5

First derivative of function is f'(x) = 6x² – 6x – 12, it will use to find out the critical points.

To find the critical point, f'(x) = 0;

6x² – 6x – 12 = 0

6(x² – x – 2) = 0

6(x + 1)(x – 2) = 0

Hence, critical points are x = -1, and x = 2.

Analyze the First derivative immediate point to the critical point x = -1. The points are {-2, 0}.

f'(-2) = 6(4 + 2 – 2) = 6(4) = +24 and f'(0) = 6(0 + 0 – 2) = 6(-2) = -12

Sign of derivative is postive towards the left of x = -1, and is negative towards the right. Hence, it indicaes x = -1 is the Local Maxima.

Let us now analyze the First derivative immediate point to the critical point x = 2. The points are {1,3}.

f'(1) = 6(1 -1 -2) = 6(-2) = -12 and f'(3) = 6(9 + -3 – 2) = 6(4) = +24

Sign of derivative is negative towards the left of x = 2, and is positive towards the right. Hence, it indicates x = 2 is the Local Minima.

Therefore, the Local Maxima is -1, and the Local Minima is 2.

Example 2: Analyze the Local Maxima and Local Minima of the function f(x) = -x³ +6x² -12x +10 by using the second derivative test.

Solution:

Given function is f(x) = -x³ +6x² -12x +10

First derivative of function is f'(x) = -x³ +6x² -12x +10, it will use to find out the critical points.

To find the critical point, f'(x) = 0;

f'(x) = -3x² + 12x -12 = 0

3(-x² + 4x – 3) = 0

x² – 4x + 3 = 0

(x – 1)(x – 3) = 0

Hence the critical points are x = 1, and x = 3

Now take a Second derivative of function,

f”(x) = 6x – 12

Evaluate f”(x) at critical point x=1

f”(1) = 6(1) – 12 = 6 – 12 = -6

f”(1) < 0, and Hence x = 1 corresponds to Local Maxima.

Evaluate f”(x) at critical point x = 3

f”(3) = 6(3) – 12 = 18 – 12 = 6

f”(3) > 0, and Hence x = 3 corresponds to Local Minima.

Now, we will calculate the Function Values at the critical points:

f(1) = -(1)³ +6(1)² -12(1) +10 = 3, Therefore, the Local maximum is at (1, 3)

f(3) = -(3)³ +6(3)² -12(3) +10 = 1, Therefore, the Local maximum is at (3, 1)

Example 3 : Find the local maxima and minima of f(x) = x³ – 6x² + 9x + 1.

Solution:

f'(x) = 3x² – 12x + 9

Set f'(x) = 0: 3x² – 12x + 9 = 0

(3x – 3)(x – 3) = 0

x = 1 or x = 3

f”(x) = 6x – 12

At x = 1: f”(1) = -6 < 0, so local maximum

At x = 3: f”(3) = 6 > 0, so local minimum

Local maximum at x = 1, f(1) = 5

Local minimum at x = 3, f(3) = 1

Example 4 : Determine the critical points of g(x) = x⁴ – 4x³ + 6x² and classify them as local maxima, local minima, or neither.

Solution:

g'(x) = 4x³ – 12x² + 12x = 4x(x² – 3x + 3)

Set g'(x) = 0: 4x(x² – 3x + 3) = 0

x = 0 or x² – 3x + 3 = 0

x = 0, 3/2 (using quadratic formula)

g”(x) = 12x² – 24x + 12

At x = 0: g”(0) = 12 > 0, so local minimum

At x = 3/2: g”(3/2) = -9 < 0, so local maximum

Example 5 : Find the absolute maximum and minimum values of h(x) = 2x³ – 3x² – 36x + 7 on the closed interval [-3, 4].

Solution:

h'(x) = 6x² – 6x – 36 = 6(x² – x – 6) = 6(x + 2)(x – 3)

Critical points: x = -2 and x = 3

Evaluate h at critical points and endpoints:

h(-3) = -110

h(-2) = 57

h(3) = -74

h(4) = -9

Absolute maximum: 57 at x = -2

Absolute minimum: -110 at x = -3

Example 6 : Locate and classify all critical points of f(x) = x²/³ – 2x.

Solution:

f'(x) = (2/3)x^(-1/3) – 2

Set f'(x) = 0: (2/3)x^(-1/3) = 2

x^(-1/3) = 3

x = 1/27

f”(x) = -(2/9)x^(-4/3)

At x = 1/27: f”(1/27) < 0, so local maximum

Example 7 : Find the local extrema of g(x) = xe^(-x²) for x ≥ 0.

Solution:

g'(x) = e^(-x²) – 2x²e^(-x²)

Set g'(x) = 0: e^(-x²)(1 – 2x²) = 0

1 – 2x² = 0

x = ±1/√2, but we only consider x ≥ 0

So, x = 1/√2

g”(x) = -2xe^(-x²)(3 – 2x²)

At x = 1/√2: g”(1/√2) < 0, so local maximum

Local maximum at x = 1/√2

Example 8 : Determine the intervals on which f(x) = x³ – 3x + 2 is increasing or decreasing.

Solution:

f'(x) = 3x² – 3 = 3(x² – 1) = 3(x + 1)(x – 1)

f'(x) = 0 when x = 1 or x = -1

f'(x) < 0 for -1 < x < 1

f'(x) > 0 for x < -1 and x > 1

Decreasing on (-1, 1)

Increasing on (-∞, -1) and (1, ∞)

Example 9 : Find the inflection points of h(x) = x⁴ – 4x³ + 6x².

Solution :

h'(x) = 4x³ – 12x² + 12x

h”(x) = 12x² – 24x + 12 = 12(x² – 2x + 1) = 12(x – 1)²

h”(x) = 0 when x = 1

h”'(x) = 24(x – 1)

h”'(1) = 0, but changes sign around x = 1

Inflection point at x = 1

Example 10 : A rectangular box with no top is to be constructed from 12 square feet of material. Find the dimensions that will maximize the volume of the box.

Solution:

Let length = x, width = y, height = z

Area equation: xy + 2xz + 2yz = 12

Volume: V = xyz

Express y in terms of x: y = (12 – 2xz) / (x + 2z)

V = xz(12 – 2xz) / (x + 2z)

∂V/∂x = 0 and ∂V/∂z = 0 lead to x = 2z

Substituting back: 4z² + 4z² + 2z² = 12

10z² = 12

z = √(6/5)

x = 2√(6/5), y = √(6/5)

Dimensions: length = 2√(6/5), width = √(6/5), height = √(6/5)

Practice Questions on Local Minima and Maxima

Q1. Find Local Maxima and Local Minima of the function f(x) = 2×3 – 3x²-12x +5 by using the second derivative test.

Q2. Find and analyze the Local Maxima and Local Minima of the function f(x) = – x²+4x -5 by using the second derivative test.

Q3. Find Local Maxima and Local Minima of the function f(x) = x²-4x +5 by using the first derivative test.

Q4. Find and analyze the Local Maxima and Local Minima of the function f(x) = 3x²-12x +5 by using the first derivative test.

Q5. Find and analyze the Local Maxima and Local Minima of the function f(x) = x³ – 6x²+9x + 15 by using the first derivative test.

Q6. Find and analyze the Local Maxima and Local Minima of the function f(x) = 2x³ -9x²+12x +5 by using the second derivative test.

Summary

Local maxima and minima in calculus are critical points on a function where it reaches its highest or lowest values within a specific interval. These concepts are fundamental for analyzing function behavior and solving optimization problems. To find these points, we typically use the first derivative test, looking for where f'(x) equals zero or is undefined. The nature of these critical points can be further classified using the second derivative test: if f”(a) < 0, it’s a local maximum; if f”(a) > 0, it’s a local minimum.

Inflection points, where the function’s concavity changes, are also important and occur where f”(x) = 0 or is undefined. When dealing with closed intervals, we must also consider the endpoints to find global extrema. These principles are widely applied in various fields, from economics and physics to engineering, helping to optimize processes, designs, and resource allocation. Understanding local maxima and minima is crucial for anyone working with functions and seeking to find optimal solutions in real-world scenarios.

Local Maxima and Local Minima – FAQs

What is Local Maxima?

A point is called a Local Maxima when the function reaches its highest value in a specific interval.

How can you find the Local Maximum?

By differentiating the function and finding the critical value at which the slope is zero, we can find find the Local Maximum.

What is Local Minima?

A point is called a Local Minima when the function reaches its lowest value in a specific interval.

What methods can you use to calculate the Local Maxima and Local Minima?

First derivative test and Second derivative test.

What is the difference between First derivative test and Second derivative test?

First derivative test is the approximate method to calculate the value of lLcal maxima and Local minima and Second derivative test is the systematic and accurate method to calculate the value of Local maxima and Local minima.

What is the Meaning of Point of Inversion?

If the value of a point within the range of given function does not show the highest and lowest output, that point is called the Point of Inversion.

What is the Use of Local Maxima and Local Minima?

To find out the extreme value of a function within a particular range.