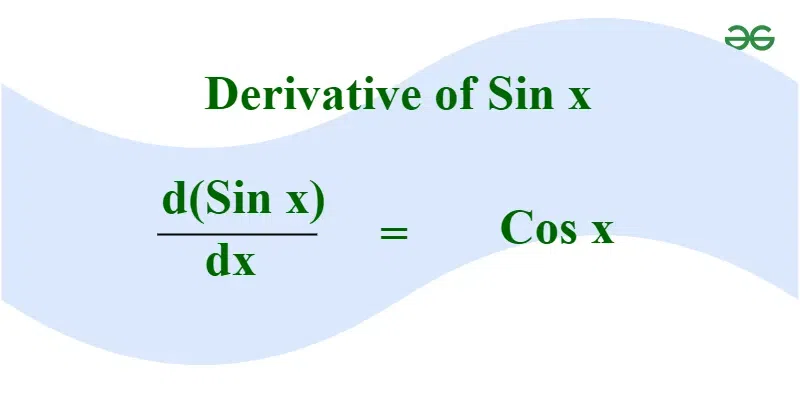
Derivative of Sin x is Cos x. It refers to the process of finding the change in the sine function with respect to the independent variable. This process is known as differentiation, which is one of the fundamental tools in calculus used to determine the rate of change for various functions. The specific process of finding the derivative for trigonometric functions is referred to as trigonometric differentiation, and the derivative of Sin x is one of the key results in trigonometric differentiation.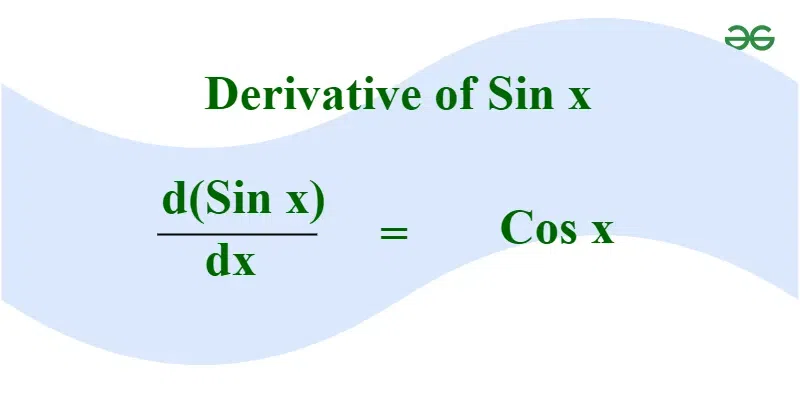

In this article, we will learn about the derivative of sin x and its formula including the proof of the formula using the first principle of derivatives, quotient rule, and chain rule as well. Other than that, we have also provided some solved examples for better understanding and answered some FAQs on derivatives of sin x as well. Let’s start our learning on the topic Derivative of Sin x.

What is Derivative in Math?

The derivative of a function is the rate of change of the function with respect to any independent variable. The derivative of a function f(x) is denoted as f'(x) or (d /dx)[f(x)]. The differentiation of a trigonometric function is called as derivative of the trigonometric function or trig derivatives.

Read More:

• Calculus in Maths
• Differential Calculus

What is Derivative of Sin x?

Among the trig derivatives, the derivative of the sinx is one of the derivatives. The derivative of the sin x is cos x. The derivative of sin x is the rate of change with respect to angle i.e., x. The resultant of the derivative of sin x is cos x.

Derivative of Sin x Formula

The formula for the derivative of sin x is given by:

(d/dx) [sin x] = cos x

or

(sin x)’ = cos x

Proof of Derivative of Sin x

The derivative of sin x can be proved using the following ways:

• By using the First Principle of Derivative
• By using Quotient Rule
• By using Chain Rule

Derivative of Sin x by First Principle of Derivative

To prove derivative of sin x using First Principle of Derivative, we will use basic limits and trigonometric formulas which are listed below:

1. sin (x + y) = sin x cos y + sin y cos x
2. lim _x→0 [sin x/x] = 1
3. lim _x→0 [(cos x – 1)/x] = 0

Let’s start the proof for the derivative of sin x

By the First Principle of Derivative

(d/dx) sin x = lim_h→0 [sin(x + h) – sinx]/[(x + h) – x]

⇒ (d/dx) sin x = lim_h→0 [sinx cosh + sinh cosx – sinx]/ h [By 1]

⇒ (d/dx) sin x = lim_h→0 [{sinx (cosh – 1)}/h + {(sinh/h) cosx}]

⇒ (d/dx) sin x = lim_h→0 {sinx (cosh – 1)}/h + lim_h→0{(sinh/h) cosx} [By 2 and 3]

⇒ (d/dx) sin x = sinx (0)+ (1)cosx

⇒ (d/dx) sin x = cosx

Derivative of Sin x by Quotient Rule

To prove derivative of sin x using Quotient rule, we will use basic derivatives and trigonometric formulas which are listed below:

1. sin x = 1/cosec x
2. (d/dx) [u/v] = [u’v – uv’]/v²

Let’s start the proof of the derivative of sin x

y = sin x

y = 1/cosec x

⇒ y’ = (d/dx) [1/cosec x]

Applying quotient rule

y’ = [(d/dx) (1) cosec x – 1.(d/dx)(cosec x)]/(cosec x)²

⇒ y’ = [(0) cosec x – (1) (-cosec x cot x)]/(cosec x)²

⇒ y’ = (cosec x cot x)/(cosec x)²

⇒ y’ = cot x/cosec x

⇒ y’ = (cos x/sin x )/( 1/sin x)

⇒ y’ = cos x

Derivative of Sin x by Chain Rule

To prove derivative of sin x using chain rule, we will use basic derivatives and trigonometric formulas which are listed below:

1. sin x = cos [(π/2) – x]
2. cos x = sin [(π/2) – x]

Let’s start the proof of the derivative of sin x

y = sin x

y = cos [(π/2) – x] {From Formula 1}

⇒ y’ = (d/dx){cos [(π/2) – x]}

By applying chain rule

y’ = (d/dx){cos [(π/2) – x]}(d/dx)[(π/2) – x]

⇒ y’ = {-sin [(π/2) – x]}(0 – 1)

⇒ y’ = {-sin [(π/2) – x]}(- 1)

⇒ y’ = sin [(π/2) – x]

⇒ y’ = cos x

Also, Check

• Differentiation of Trigonometric Functions
• Derivative of Inverse Trigonometric Functions
• Differentiation Formulas
• Derivative of Sin x
• Differentiation of Trigonometric Functions

Examples on Derivative of Sin x

Example 1: Find the derivative of sin 4x.

Solution:

Let y = sin 4x

⇒ y’ = (d/dx) [sin 4x]

Applying chain rule

y’ = (d/dx) [sin 4x].(d/dx) (4x)

⇒ y’ = (cos 4x)4

⇒ y’ = 4cos4x

Example 2: Evaluate the derivative f(x) = (x³ + 5x² + 2x + 7)sinx

Solution:

f(x) = (x³ + 5x² + 2x + 7)sinx

⇒ f'(x) = (d /dx)[(x³ + 5x² + 2x + 7)sinx]

Applying product rule

f'(x) = (d /dx)[(x³ + 5x² + 2x + 7)]sinx + (x³ + 5x² + 2x + 7)(d /dx)[sinx]

⇒ f'(x) = (3x² + 10x +2)sinx + (x³ + 5x² + 2x + 7)cosx

Example 3: Find the derivative of p(x) = (4x² + 9)/sinx

Solution:

p(x) = (4x² + 9)/sinx

⇒ p'(x) = (d /dx)[(4x² + 9)/sinx]

Applying quotient rule

p'(x) = [(d /dx)(4x² + 9) sin x – (4x² + 9)(d /dx)sin x]/ sin²x

⇒ p'(x) = [8xsin x – (4x² + 9)cos x]/ sin²x

Example 4: Find the derivative of the function (cosx)^sinx

Solution:

Let y = (cosx)^sinx

Taking log

ln y = ln (cosx)^sinx

⇒ ln y = (sin x) ln (cos x)

Differentiating the above equation, we get

(1/y) y’ = (d/dx)[(sin x) ln (cos x)]

Applying product rule

(1/y) y’ = (d/dx)(sin x) [ln (cos x)]+ (sin x)(d/dx)[ln (cos x)]

⇒ (1/y) y’ = cos x [ln (cos x)]+ (sin x)[(-sinx)/(cos x)]

⇒ (1/y) y’ = cos x {ln (cos x)} – sin x tan x

⇒ y’ = y[cos x {ln (cos x)} – sin x tan x]

⇒ y’ = (cosx)^sinx [cos x {ln (cos x)} – sin x tan x]

Example 5: Evaluate the derivative sin 5x + x.sinx

Solution:

Let z = sin 5x + xsinx

Differentiating

z’ = (d/dx) [sin 5x + xsinx]

⇒ z’ = (d/dx) sin 5x + (d/dx)[xsinx]

Applying chain rule and product rule

z’ = 5 cos 5x + (d/dx)(x)sinx + x(d/dx)(sinx)

⇒ z’ = 5 cos 5x + sinx + xcosx

Example 6: Find derivative of sin^-1 x.

Solution:

(d /dx) [sin^-1 x] = 1/√[1 – x²] [From Formula]

Example 7: Find derivative of sin x²

Solution:

By applying chain rule

(d/dx) [sin x²] = (d/dx) [sin x²](d/dx) [x²]

⇒ (d/dx) [sin x²] = [cos x²][2x]

⇒ (d/dx) [sin x²] = 2x cos x²

Example 8: Find derivative of sin x. cos x

Solution:

By applying product rule

(d/dx) [sin x. cos x] = (d/dx) [sin x] cos x + sin x (d/dx) [cos x]

⇒ (d/dx) [sin x. cos x] = cos x. cos x + sin x (-sin x)

⇒ (d/dx) [sin x. cos x] = cos² x – sin² x

⇒ (d/dx) [sin x. cos x] = cos 2x

Example 9: Find derivative of x sin x

Solution:

By applying product rule

⇒ (d/dx) [x sin x] = (d/dx) [x] sin x + x (d/dx) [sin x]

⇒ (d/dx) [x sin x] = (1) sin x + x cos x

⇒ (d/dx) [x sin x] = sin x + x cos x

Example 10: What is derivative of sin x and cos x

Solution:

(d/dx) sin x = cos x

⇒ (d/dx) cos x = -sin x

Practice Questions on Derivative of Sin x

Q1. Find the derivative of sin 7x

Q2. Find the derivative of x².sinx

Q3. Evaluate: (d/dx) [sin x/(x² + 2)]

Q4. Evaluate the derivative of: sin x. tan x

Q5. Find: (tan x)^{sin x}

Conclusion

The derivative of the sine function, sin⁡(x), is the cosine function, cos⁡(x). Mathematically, if f(x)=sin(x), then f′(x)=cos⁡(x). This result comes from the limit definition of the derivative and the fundamental properties of trigonometric functions. The derivative of sin(x) is cos(x).The relationship is pivotal in calculus, especially in solving problems involving periodic motion, wave analysis, and oscillations. The fact that the derivative of sin⁡(x) is cos⁡(x) also reflects the intrinsic connection between these two functions, as they are phase-shifted versions of each other.Derivative of sin(x) tells you something about the rate of change of the sine function at any given point. If sine is a wave, cosine tells you whether the wave is rising, falling, or at a peak/trough at any given point. Imagine the sine function as a wave. The derivative, cosine, tells you if the wave is currently going up, down, or is flat (neither going up nor down).

Derivative of Sin x – FAQs

What is Derivative?

The derivative of the function is defined as the rate of change of the function with respect to a variable.

Write the Formula for Derivative of Sin x.

The formula for derivative of sin x is:

(d/dx) sin x = cos x

What is the Derivative of Sin (-x)?

Derivative of sin (-x) is -cos (-x) or -cos x.

What are the Different Methods to Prove Derivative of Sin x?

The different methods to prove derivative of sin x are:

• By using First Principle of Derivative
• By Quotient Rule
• By Chain Rule

What is the Derivative of Negative Sin x?

Derivative of negative sin x i.e., -sin x; is -cos x.

What is Derivative of Cos x?

Derivative of cos x -sin x.

What is the Derivative of 2 sin x?

Derivative of 2 sin x is 2 cos x.

What is the Derivative of Tan x?

Derivative of tan x is sec² x.