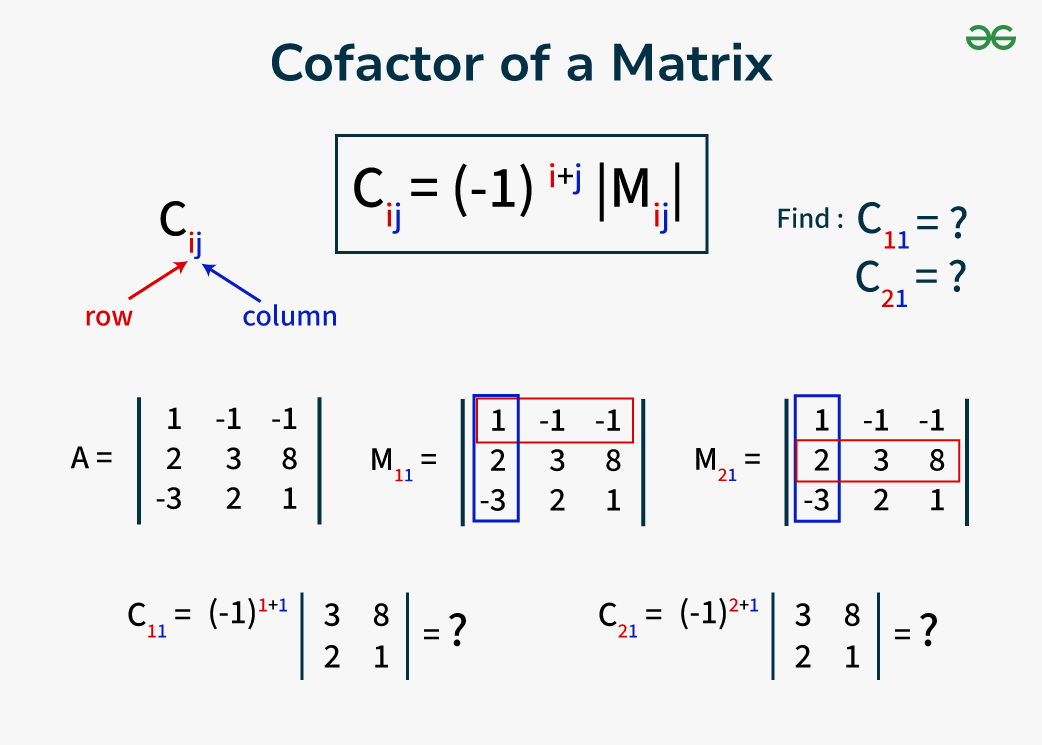
The cofactor of a Matrix is an important concept in linear algebra. It is often used in calculating the determinant and the inverse of a matrix. Cofactor of Matrix or Cofactor matrix is the matrix formed by the Cofactor of each element of any matrix where cofactor is a number that is obtained by multiplying the minor of the element of any given matrix with -1 raised to the power of the sum of the row and column number to which that element belongs. This matrix formed with the cofactor of each element is called the Cofactor Matrix or Cofactor of Matrix.

Cofactor of a Matrix

Cofactors and Minors are very important concepts in Linear Algebra which further help us find the determinants, adjoint, and inverse of the matrix as well. We have explained in detail about Cofactor of a Matrix.

Cofactor of Matrix

A cofactor matrix is a matrix that comprises the cofactors of each element in a matrix. A cofactor is a number obtained when the minor M_ij of the element a_ij is multiplied by the (-1)^i+j. i and j represent the row and column of the particular element whose cofactor is being determined. Minor of an element is obtained by eliminating the row and column of that particular element i.e. eliminating row i and column j and then taking the remaining part of the matrix. Then we calculate the determinant of the remaining part which gives us the value of the minor of that particular element. 

Cofactor of Matrix Definition

The cofactor of an element in a matrix is determined by the minor of that element, which is essentially the determinant of the submatrix obtained by removing the row and column containing the element in question.

Formula for Cofactor of a Matrix

If we denote the Cofactor using C_ij, then the cofactor of any element for 

C_ij = M_ij × (-1)^i+j

Where,

• i is the number of rows for the element under consideration,
• j is the number of columns for the element under consideration, and
• M_ij is the minor of the element in the i^th row and j^th column.

What is Minor?

A minor of a particular element is obtained by eliminating the row and column of the matrix to which that particular element belongs and then finding the determinant of the remaining part. The matrix formed by combining all the minors is called the minor matrix. For example minor of the element a11 matrix [Tex]\begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix}    [/Tex]is calculated as:

[Tex]M_{11} = det\begin{bmatrix} 5 & 6\\ 8 & 9 \end{bmatrix}\\ = 45-48\\ = -3 [/Tex]

How to Find Cofactor of Matrix?

In order to find a cofactor matrix we need to perform the following steps:

• Step 1: Find the minor of each element of the matrix and make a minor matrix.
• Step 2: Multiply each element in the minor matrix by (-1)^i+j_.
• Thus, we obtain the cofactor matrix.

Let us understand how to find a cofactor matrix using an example:

Example: Find the cofactor matrix of [Tex]\begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix} [/Tex]

Solution:

• Step 1: Find the minor of each element and make a minor matrix.

Minor of a₁₁ is calculated by eliminating row 1 and column 1 and taking the determinant of the remaining matrix as follows:

M₁₁ = determinant of [Tex]\begin{bmatrix} 5 & 6\\ 8 & 9 \end{bmatrix} [/Tex]

M₁₁ = 5(9) – 6(8)

M₁₁ = 45 – 48 = -3

• Similarly, the minor of element a₁₂ is calculated by eliminating row 1 and column 2 and taking the determinant of the remaining matrix as follows:

M₁₂ = determinant of [Tex]\begin{bmatrix} 4 & 6\\ 7 & 9 \end{bmatrix} [/Tex]

M₁₂ = 4(9) – 6(7)

M₁₂ = 36 – 42 = -6

• Similarly, calculate the minors of all elements to obtain the following minor matrix:

[Tex]\begin{bmatrix} -3 & -6 & -3\\ -6 & -12 & -6\\ -3 & -6 & -3 \end{bmatrix} [/Tex]

• Step 2: Multiply each element of the minor matrix by (-1)^i+j to get the cofactor of that element i.e. C_ij
• Cofactor of M₁₁ is calculated as follows:

C₁₁ = M₁₁ × (-1)¹⁺¹ = M₁₁ = -3

• Cofactor of M₁₂ is calculated as follows:

C₁₂ = M₁₂ × (-1)¹⁺² = -M₁₂ = 6

• Similarly, calculate the other cofactors to obtain the following cofactor matrix:

[Tex]\begin{bmatrix} -3 & 6 & -3\\ 6 & -12 & 6\\ -3 & 6 & -3 \end{bmatrix} [/Tex]

Cofactor of 2×2 Matrix

Consider a 2×2 matrix as follows:

[Tex]A = \begin{bmatrix} a & b\\ c & d \end{bmatrix} [/Tex]

Then the cofactor matrix of any such matrix is written as:

[Tex]C = \begin{bmatrix} a & -b\\ -c & d \end{bmatrix} [/Tex]

Cofactor of 3×3 Matrix

Consider a 3×3 matrix as follows:

[Tex]A = \begin{bmatrix} a & b & c\\ d & e&f\\ g&h&i \end{bmatrix} [/Tex]

Then the cofactor matrix of any such matrix is calculated by calculating the cofactors of each of the elements as follows:

Let M_ij denote the minor of the element in row i and column j, then in the above matrix:

[Tex]M_{11} = det \begin{bmatrix} e&f\\ h&i \end{bmatrix} [/Tex]

[Tex]M_{12} = det \begin{bmatrix} d&f\\ g&i \end{bmatrix} [/Tex]

Similarly, we can calculate the minors of all the elements to get the below minor matrix:

[Tex]M = \begin{bmatrix} M_{11} & M_{12} & M_{13}\\ M_{21} & M_{22}&M_{23}\\ M_{31}&M_{32}&M_{33} \end{bmatrix} [/Tex]

Now cofactor of each element is calculated by multiplying the minor from the minor matrix with -1 raised to the power of the sum of row and column numbers to which that minor belongs as follows:

Let C_ij denote the cofactor of minor M_ij, then:

C₁₁ = (-1)¹⁺¹M₁₁ = M₁₁
C₁₂ = (-1)¹⁺²M₁₂ = -M₁₂
C₁₃ = (-1)¹⁺³M₁₃ = M₁₃

Similarly, after calculating all the cofactors of each element we get the following cofactor matrix:

[Tex]C= \begin{bmatrix} C_{11} & C_{12} & C_{13}\\ C_{21} & C_{22} & C_{23}\\ C_{31} & C_{32} & C_{33} \end{bmatrix} [/Tex]

Applications of Cofactor of a Matrix

There are various applications of Cofactor Matrix. Some of these applications are:

• Cofactor of the Matrix is used to find the adjoint of the matrix.
• Cofactor Matrix is used in the calculation of determinant of the matrix.
• It is also used to find the inverse of the matrix.

Must Read

• Types of Matrix
• Transpose of Matrix

Solved Examples on Cofactor of a Matrix

Example 1. Find the cofactor of a₁₁ in the matrix [Tex]\begin{bmatrix} 1 & 3\\ 5 & 7 \end{bmatrix} [/Tex]

Given matrix is [Tex]\begin{bmatrix} 1 & 3\\ 5 & 7 \end{bmatrix} [/Tex]

Minor M₁₁ = 7

Cofactor of a₁₁ = 7 × (-1)¹⁺¹ = 7

Example 2. Find the cofactor of a₂₂ in the matrix [Tex]\begin{bmatrix} 1&4 & 6\\ 8 & 7 & 9 \\ 4 & 0 & 5 \end{bmatrix} [/Tex]

Given matrix is [Tex]\begin{bmatrix} 1&4 & 6\\ 8 & 7 & 9 \\ 4 & 0 & 5 \end{bmatrix} [/Tex]

Minor M₂₂ = determinant of [Tex]\begin{bmatrix} 8 & 9 \\ 4 & 5 \end{bmatrix} [/Tex]

M₂₂ = 40 – 36 = 4

Cofactor C₂₂ of a₂₂ = M₂₂ × (-1)²⁺¹

C₂₂ = 4 × (-1) = -4

Example 3. What is the cofactor matrix of [Tex]\begin{bmatrix} 3 & 6\\ 7 & 8 \end{bmatrix} [/Tex]

Step 1: Find the minor of each element and make a minor matrix.

Minor of a₁₁ is calculated by eliminating the row 1 and column 1 as follows

M₁₁ = 8

Similarly minor of element a₁₂ is calculated by eliminating the row 1 and column 2 as follows:

M₁₂ = 7

Similarly calculate minors of all elements to obtain the following minor matrix:

[Tex]\begin{bmatrix} 8 & 7\\ 6 & 3 \end{bmatrix} [/Tex]

Step 2: Multiply each element of the minor matrix by (-1)^i+j to get the cofactor of that element i.e. C_ij

Cofactor of M₁₁ is calculated as follows:

C₁₁ = M₁₁ × (-1)¹⁺¹ = M₁₁ = 8

Cofactor of M₁₂ is calculated as follows:

C₁₂ = M₁₂ × (-1)¹⁺² = -M₁₂ = -7

Similarly calculate the other cofactors to obtain the following cofactor matrix:

[Tex]\begin{bmatrix} 8 & -7\\ -6 & 3 \end{bmatrix} [/Tex]

Example 4. What is the cofactor matrix of [Tex]\begin{bmatrix} 0 & -6\\ -3 & -4 \end{bmatrix} [/Tex]

Step 1: Find the minor of each element and make a minor matrix.

Minor of a₁₁ is calculated by eliminating the row 1 and column 1 as follows

M₁₁ = -4

Similarly minor of element a₁₂ is calculated by eliminating the row 1 and column 2 as follows:

M₁₂ = -3

Similarly calculate minors of all elements to obtain the following minor matrix:

[Tex]\begin{bmatrix} -4 & -3\\ -6 & 0 \end{bmatrix} [/Tex]

Step 2: Multiply each element of the minor matrix by (-1)^i+j to get the cofactor of that element i.e. C_ij

Cofactor of M₁₁ is calculated as follows:

C₁₁ = M₁₁ × (-1)¹⁺¹ = M₁₁ = -4

Cofactor of M12 is calculated as follows:

C₁₂ = M₁₂ × (-1)¹⁺² = -M₁₂ = -3

Similarly calculate the other cofactors to obtain the following cofactor matrix:

[Tex]\begin{bmatrix} -4 & 3\\ 6 & 0 \end{bmatrix} [/Tex]

Example 5. What is the cofactor matrix of [Tex]\begin{bmatrix} 2&4 & 6\\ 7 & 9&2\\ 1& 6 & 0 \end{bmatrix} [/Tex]

Step 1: Find the minor of each element and make a minor matrix.

Minor of a₁₁ is calculated by eliminating the row 1 and column 1 and taking determinant of remaining matrix as follows:

M₁₁ = determinant of [Tex]\begin{bmatrix} 9 & 2\\ 6 & 0 \end{bmatrix} [/Tex]

M₁₁ = 0 -12 = -12

Similarly minor of element a₁₂ is calculated by eliminating the row 1 and column 2 and taking determinant of remaining matrix as follows:

M₁₂ = determinant of [Tex]\begin{bmatrix} 7 & 2\\ 1 & 0 \end{bmatrix} [/Tex]

M₁₂ = 0 – 2 = -2

Similarly calculate minors of all elements to obtain the following minor matrix:

[Tex]\begin{bmatrix} -12 & -2 & -33\\ -36 & -6 & 8\\ -46 & -38 & -10 \end{bmatrix} [/Tex]

Step2 : Multiply each element of the minor matrix by (-1)^i+j to get the cofactor of that element i.e. C_ij

Cofactor of M₁₁ is calculated as follows:

C₁₁ = M₁₁ × (-1)¹⁺¹ = M₁₁ = -12

Cofactor of M₁₂ is calculated as follows:

C₁₂ = M₁₂ × (-1)¹⁺² = -M₁₂ = 2

Similarly calculate the other cofactors to obtain the following cofactor matrix:

[Tex]\begin{bmatrix} -12 & 2 & -33\\ 36 & -6 & -8\\ -46 & 38 & -10 \end{bmatrix} [/Tex]

Practice Problems on Cofactor of a Matrix

Problem 1: Find the cofactor of the element in the second row and third column: [Tex]A = \begin{bmatrix} 2 & 3 & 4\\ 6 &6 & 5\\ 7 & 8 & -10 \end{bmatrix} [/Tex].

Problem 2: Find the cofactor matrix of [Tex]A = \begin{bmatrix} 12 & 7 & 4\\ 4 &1 & 5\\ 7 & 0 & 5 \end{bmatrix} [/Tex].

Problem 3: Find the cofactor matrix of [Tex]A = \begin{bmatrix} 4 & 0 & 1\\ 16 &2 & 9\\ 8 & 3 & 7 \end{bmatrix} [/Tex].

Problem 4: Find the cofactor matrix of [Tex]A = \begin{bmatrix} 1 & 0 & 0\\ 1 &0 &1\\ 4& 1 & 6 \end{bmatrix} [/Tex].

Problem 5: Find the cofactor matrix of [Tex]A = \begin{bmatrix} 3 & 5 & 7\\ 9 &11 & -13\\ -17 & 19 & 23 \end{bmatrix} [/Tex].

Cofactor of a Matrix – FAQs

What is Cofactor of Matrix?

Cofactor matrix is the matrix formed by the Cofactor of each element of any matrix where cofactor is a number that is obtained by multiplying the minor of the element of any given matrix with -1 raised to the power of the sum of the row and column number to which that element belongs.

What is the Formula for the Cofactor of Element?

For any element in i^th row and j^th column, its cofactor is given by C_ij = M_ij × (-1)^i+j.

How do you Find the Cofactor of a Matrix?

To find the cofactor of a matrix, first calculate the determinant of the matrix formed by excluding the row and column of the element for which you want the cofactor. Then, apply the appropriate sign (+/-) based on the element’s position in the matrix.

How can we Find Adjoint using Cofactor Matrix?

Adjoint of the matrix is calculated by taking the transpose of the cofactor matrix.

What is the Cofactor of 2×2 matrix?

If [Tex]\begin{bmatrix} a & b\\ c & d \end{bmatrix}    [/Tex]is a 2×2 matrix then its cofactor matrix is [Tex]\begin{bmatrix} a & -b\\ -c & d \end{bmatrix} [/Tex]

What are Some Applications of the Cofactor Matrix?

Cofactor matrix has the following applications:

• To find the adjoint of the matrix.
• To calculate determinant of the matrix.
• To find the inverse of the matrix.

What is minor. How is it different from co-factor of matrix?

The minor of a matrix is the determinant of the matrix formed by excluding the row and column of the element for which you want to find the cofactor, whereas the co-factor is the same as the minor, but its sign is changed based on the position of the element.