Infinte set is one of the types of Sets based upon the cardinality in Set Theory and sets are one of the important topics in mathematics. In simple words, an infinite set is a set with infinite elements i.e., the number of elements in an infinite set never depletes. This concept of infinite sets seems to be complicated at first sight but we’ll try our best to make it as comprehensive and understanding as possible.

This article deals with this concept and tries its best to explain the concept in detail. Other than that, this article covers definition, notation, types, cardinality, examples, and properties of Infinite Sets. So, let’s start learning about Infinite Sets.

What are Infinite Sets?

In set theory, all sets that contain either an uncountable number of elements or if countable then an unlimited number of elements are called infinite sets. In other, words, infinite sets are those sets that go on indefinitely and never deplete, however finite elements we removed.

One of the most common examples of an infinite set is a set of all natural numbers i.e., N. This set is one of the first sets introduced in set theory and used throughout to define many structures and objects. Other than a set of natural numbers, a set of integers (Z) and a set of rational numbers (Q) are also examples of infinite sets.

Learn more about Set Theory.

Infinite Sets Definition

A set of elements A is said to be infinite if the elements of its proper subset A’ can be put into one-to-one correspondence with the elements of A.

If an infinite set can be put into one-to-one correspondence with the set of natural numbers, then the infinite set is called a countable infinite set otherwise it is called an uncountable infinite set.

Infinities can be of different sizes or levels, for example, a set of Real Numbers (R) is a larger infinity than a set of Natural or Rational Numbers, but both the set of natural numbers and rational numbers, are the same size sets, as both have the same cardinality.

Infinite Set Notation

The infinite sets are denoted by using dots (. . .) at the end of the elements which follow a pattern. Any set A which is an infinite set can be represented as follows:

A = {a₁ , a₂ , a₃ , . . . }

Let A be an infinite set then it is denoted as A = {1, 2, 3, . . .}, here we can see that 1, 2, 3, . . . is a common pattern that leads to further elements such as 4, 5, 6, and so on. Thus, there are infinitely many elements of set A, which can simply be represented by {1, 2, 3, . . .}.

Infinite Set Examples

Some examples of infinite sets are:

• Natural Numbers: The set of natural numbers (N) represents the counting numbers, starting from 1 and going on infinitely (1, 2, 3, 4, …).
• Prime Numbers: The set of prime numbers is an infinite set that contains numbers greater than 1 that have no divisors other than 1 and themselves (e.g., 2, 3, 5, 7, 11, 13, …).
• Integers: The set of integers (Z) includes all positive and negative whole numbers and zero i.e., { . . . -3, -2, -1, 0, 1, 2, 3, . . .}.
• Rational Numbers: The set of rational numbers (Q) includes all numbers that can be expressed as a fraction of two integers, such as 1/2, -3/4, 5/7, etc.
• Irrational Numbers: The set of irrational numbers consists of numbers that cannot be expressed as a fraction of two integers, such as √2, π, and e.
• Real Numbers: The set of real numbers (R) contains all numbers, both rational and irrational, such as 3.14, √2, π, e, etc.
• Cantor Set: Cantor Set is a mathematical construct created by removing the middle third of a line segment repeatedly, forming an infinite set of points. It is self-replicating and has a surprising property of being uncountably infinite yet having zero length on the number line.

Types of Infinite Sets

Infinite Sets are classified into two categories that are:

• Countable Infinite Set
• Uncountable Infinite Set

Countable Infinite Set

A set X is called a countable infinite set if and only if set A has the same cardinality as N (natural numbers). Some examples of countable infinite sets are a set of natural numbers N, a set of integers Z, etc.

Note: (Countable Set) A set is countable if and only if it is finite or countable infinite.

Uncountable Infinite Set

A set which can’t be mapped to the set of natural number is called the Uncountable Infinite Set. We can also say that, an uncountable infinite set is a set that is not countable. The set of real numbers R is one of the examples of an uncountable infinite set.

Cardinality of Infinite Set

The number of elements in the set is called the cardinality of the set. For example, if A = {1, 3, 4} then |A| = 3. For a major time in the history of academics, scholars only associated this concept of cardinality with finite sets, as it only seems logical. But a man with a vision to revolutionize the understanding the infinity came and the name of the man is Georg Cantor. He revolutionized the concept of the infinite in the context of sets and their cardinalities. He devised the use of ℵ to present the cardinality of infinite sets.

Cardinality of countably infinite set = ℵ₀

ℵ₀ = |N| = |Q| = |Z|

Cardinality of lowest uncountably infinite set = ℵ₁ OR C (Continuum)

C OR ℵ₁ = |R| = |P(N)|

Cardinality of uncountably infinite set = ℵ₂

ℵ₂ = |P(P(N))|

Continuum Hypothesis

The Continuum Hypothesis states that there is no set whose cardinality is strictly between that of the set of natural numbers (denoted by ℵ₀) and the set of real numbers (denoted by C i.e., Continuum). This is proposed by the great mathematician Georg Cantor in 1878 as part of his groundbreaking work on the theory of infinite sets.

The Continuum Hypothesis can be stated as follows:

• ℵ₀ = |N| (cardinality of the natural numbers)
• C = |R| (cardinality of the real numbers)

The Continuum Hypothesis claims that there is no set A such that ℵ₀ < |A| < C.

Properties of Infinite Sets

Various properties of Infinite sets are discussed below,

• Any subset of a countable set is countable.
• A superset of an uncountable set is uncountable.
• If A is an infinite set (either countable infinite or uncountable infinite), then the set of A is uncountable infinite.
• The union of two or more countable sets is countable.
• The cartesian product of two countable sets is countable.
• If A is an uncountable infinite set and B is any set, then the cartesian product of A and B is also uncountable infinite.
• ℵ₁ = 2^ℵ0

How to Check If a Set Is Finite or Infinite?

To check whether a set is finite or infinite, we use the following methods:

For Finite Sets

To verify that a set is finite, follow these steps:

• If you can list or count all the elements of the set, then the given set is a finite set.
• If the set is described using set-builder notation, check if the condition results in a finite set.
  • For example, {x | x is an even number between 1 and 10} is finite because you can list all the even numbers between 1 and 10 i.e., {2, 4, 6, 8}

For Infinite Sets

Here are a few common methods to identify infinite sets:

• Observe Patterns: If any set follows a specific pattern for its element without any end, it should be an infinite set.
  • For example, the set of natural numbers {1, 2, 3, 4, …} is infinite as you can see the pattern of adding 1 to each further element without any end.
• Bijection with a known infinite set: If you can establish a one-to-one and onto correspondence (bijection) between the given set and a known infinite set, then the given set is also infinite.
  • For example, we can establish the bijection between a set of integers and natural numbers and we know that the set of natural numbers is the infinite set. Thus, a set of integers is also an infinite set.
• Using Mathematical Properties: If the set has a property it can help us establish that this set has an infinite number of elements.
  • For example, we know that between any two rational or real numbers there are infinitely many rational or real numbers respectively. Thus the set of rational numbers between 1 and 2 and real numbers between 0 and 1 both are infinite sets.

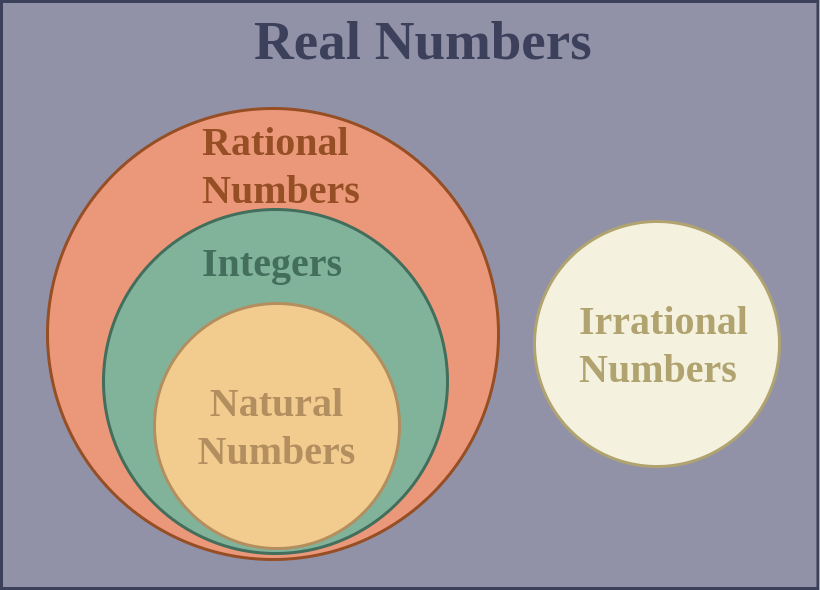
Venn Diagram for Infinite Sets

As infinite sets can’t be contained due to the limitless number of elements in it. We can only represent infinite sets in the Venn diagram when comparing the sets or representing them in relation to other sets. One such example is illustrated in the following diagram.

Difference Between Finite Sets and Infinite Sets

Finite sets are sets that can be put into one-to-one correspondence with any set of natural numbers. Infinite sets are sets that cannot be empty and cannot be put into one-to-one correspondence with any set of natural numbers. Example of a finite set: P = {5, 9, 11}. Example of infinite set X = {s, r, t, …}.