Alternate Exterior Angles in maths are generated when a transversal connects two or more parallel lines at different locations. Alternate exterior angles are a pair of angles that lie on the opposite sides of a transversal line and on the outer sides of two intersecting lines. When a transversal line intersects two other lines, it creates several pairs of angles, and alternate exterior angles are one of these pairs. You can also check the article on parallel lines and traversal to study it in detail.

The phrase exterior refers to something that is located on the outside. They are placed on opposing sides of the transversal and lie outside the two crossed lines. As a result, the two external angles formed at the opposite ends of the transversal in the outside component are termed a pair of alternative exterior angles and are always equal. When a transversal intersects two parallel lines, we obtain two such pairs of alternate exterior angles.

In this article, you will study what are alternate exterior angles, the alternate exterior angles theorem, and examples of alternate exterior angles.

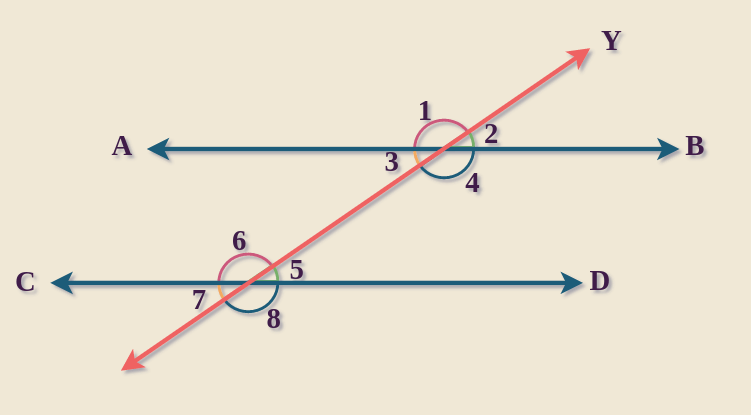
What are Alternate Angles in Geometry?

A transversal is a line formed by the intersection of two or more parallel lines. Several pairs of angles are formed when a transversal is made over parallel lines. When a transversal intersects two parallel lines, it creates four interior angles on the inside and four external angles on the outside. These are called alternate angles.

To illustrate the concept, the two parallel lines a transversal xy cuts ab and cd in the illustration below. The external angles are angles ∠1, ∠2, ∠7, and ∠8. The inner angles are angles ∠3, ∠4, ∠5, and ∠6.

Alternate Angles Definition in Geometry

Alternate angles are the angles formed by intersecting lines and a transversal line, refer to a pair of angles that are located on opposite sides of the transversal line and on different lines.

Angles ∠3 and ∠6, ∠4 and ∠5, ∠1 and ∠8, and ∠2 and ∠7 are alternates.

Read More,

• Parallel Lines
• Parallel Lines and Traversal

Types of Alternate Angles

There are two types of alternative angles:

Alternate Interior Angles: Angles on the inside of two parallel lines but on opposite sides of the transversal.

Take note of the specified angles and how each pair of angles is equal to each other.

Alternate Exterior Angles: The pair of angles on the outer edge of two parallel lines but on opposite sides of the transversal.

Take note of the alternate exterior angles and how they are equal to each other.

What are Alternate Exterior Angles in Geometry?

Angles created on the outside side of the transversal on various sides are known as alternate external angles. When two parallel lines meet at a transversal, they form certain pairs of angles with the transversal. Interior angles are formed in the space between parallel lines, whereas exterior angles are formed in the space between parallel lines.

Line ‘n’ || Line ‘m’ and are crossed by the transversal ‘o’ in the image below. The other exterior angle pairings in this case are ∠1 & ∠8 and ∠2 & ∠7. This suggests that ∠1 = ∠8 and ∠2 = ∠7.

We may deduce that ∠2 and ∠7 are opposite exterior angles. The ∠2 is on the right side of the transversal y, while the ∠7 is on the left. That is, they are on opposite sides of the transversal, with ∠2 above the line AB and ∠7 below the line CD. That is, they are outside of the two lines.

The same logic holds true for the other pair of angles (∠1 and ∠8). As a result, the pair of angles that meet these characteristics is known as an alternative exterior angle.

Alternate Exterior Angles Definition

Alternate exterior angles are two exterior angles on two independent lines cut by a transversal and placed on opposite sides of the transverse.

We can see in the image that the pairings ∠1 & ∠8 and ∠2 & ∠7 are alternative exterior angles because:

• Both are on the outside of the lines, and
• They are on different sides of the transversal.

Alternate Exterior Angles Theorem

“If two lines are parallel and intersected by a transversal, then the alternate exterior angles are considered congruent angles or angles of equal measure,” according to the alternate exterior angle theorem.

In other words, alternate exterior angles are congruent with each other. Using the same figure as before, we can see that ∠1 & ∠8 and ∠2 & ∠7 are pairs of opposite exterior angles. Let’s look at how they’re congruent (equal).

Given: AB and CD parallel lines on a transversal Y.

[Hint: The following axioms will be used to establish the above theorem:

When two lines are parallel, the corresponding angles are congruent, according to the Corresponding Angle Axiom.

When the corresponding angles created by two lines are congruent, the lines are parallel.] 

To Prove: ∠1 = ∠8

Proof: To demonstrate this conclusion, consider the vertically opposite angle of 1.

In this case, the vertically opposite angle of ∠1 is ∠4.

As a result, ∠1 = ∠4 (vertically opposed angles).

In this case, line AB || CD, 

∠4 = ∠8 (which corresponding angles axiom) 

∠1 = ∠8 (transitivity)

As a result, ∠1 = ∠8 proved.

Converse of Alternate Exterior Angles Theorem

If the alternate exterior angles created by two lines cut by a transversal are congruent, the lines are parallel, according to the converse of the alternate exterior angle theorem.

As a result, in the preceding diagram, if ∠1 = ∠8, then line AB || line CD.

There is one more form of external angle pair besides alternative exterior angles. This is known as a pair of consecutive exterior angles (or co-exterior angles). In the illustration above, there are two sets of sequential external angles.

∠2 and ∠8;

∠1 and ∠7

Exterior angles that are consecutive are supplementary, i.e., ∠2 + ∠8 = 180° and ∠1 + ∠7 = 180°.

Are Alternate Exterior Angles Congruent?

Alternate exterior angles are congruent. This congruence property holds true when two lines are parallel and when they are not. In the case of parallel lines, alternate exterior angles are always congruent because of the relationship between parallel lines and transversals.

Let’s illustrate the concept of congruent alternate exterior angles with a few examples:

Example 1: Parallel Lines

Consider two parallel lines, Line AB and Line CD, intersected by a transversal Line EF:

In this scenario, ∠1 and ∠2 are alternate exterior angles. Due to the congruence property, ∠1 is congruent to ∠2. Therefore, if ∠1 measures 60 degrees, ∠2 will also measure 60 degrees.

Example 2: Non-Parallel Lines

Now, let’s consider two non-parallel lines, Line PQ and Line RS, intersected by a transversal Line MN:

In this case, ∠3 and ∠4 are also alternate exterior angles. Although the lines are not parallel, ∠3 and ∠4 are still congruent due to the alternate exterior angle property. If ∠3 measures 45 degrees, ∠4 will also measure 45 degrees.

Interesting Facts about Alternate Exterior Angles

Some of the interesting facts about Alternate Exterior Angles are listed as follows:

• If the lines traversed by the transversal are parallel, alternate exterior angles are congruent.
• If the outside angles of the lines are congruent, the lines are parallel.
• The appropriate angles are located in the same location at each junction.
• The transversal intercepts the alternate outer angles that fall outside the lines.
• These angles are in addition to the neighboring angles.

Also, Check

• Types of Angles
• Lines and Angles
• Consecutive Interior Angles

Alternate Exterior Angles Examples

Example 1: Demonstrate that the exterior angles (4x + 52) ° and (5x – 66) ° are congruent.

Answer:

Interior alternate angles are equal, As a result, 

(4x + 52) ° = (5x – 66) ° 

⇒ 4x + 52 = 5x – 66 

⇒ x = 118

In the original formulations, substitute x.

⇒ (4x + 52) ° = 524°.

⇒ (5x – 66) ° = 524°

As a result, (4x + 52) ° = (5x – 66) °.

Example 2: Mark the exterior angles and write their values on the accompanied picture. In the diagram, ∠1 = 45°and ∠2 = 135°.

Answer:

The various outside angles in the preceding image are  ∠1, ∠2, ∠8, and ∠7. Only ∠1 and ∠2 are offered.

Because we already know that alternate outside angles are equivalent.

So, ∠1 = ∠7 = 45°

      ∠2 = ∠8 = 135°

Example 3: If the alternate exterior angles are indicated as (4x + 48)° and (5x – 55)° in a given set of two parallel lines cut by a transversal, calculate the value of x and the true value of the alternate exterior angles using the alternate exterior angles theorem.

Answer:

Alternate interior angles are (4x + 48)° and (5x – 55)°. The two angles are congruent because L1 and L2 are parallel. So, 

(4x + 48)° = (5x – 55)° 

⇒ 4x + 48 = 5x – 55 

⇒ -103 = -x 

As a result, x = 103 degrees.

We may obtain the precise value of the angles by replacing the value of x with the supplied angles.

(4x + 48)° = [4(103) + 48]° = 460° 

(5x – 55)°= [5(103) − 55]° = 460°

Because they are opposite outside angles, they have the same value.

Example 4: A and B are on opposite lanes. They intended to build a route that would cut between the two paths at an angle. What is the value of ∠B if ∠A = 65°?

Answer:

Because the two pathways are joined by a transversal, the alternative angles should be identical, suggesting that ∠A equals ∠B.

As a result, ∠B = ∠A = 65°.

Example 5: Determine all alternate exterior angles.

Answer:

First, we must determine our outside angles. We can see that ∠5, ∠6, ∠3, and ∠9 are all positioned outside lines r and e.

However, because we are requested to identify the alternate outside angles, we must include the pairs of angles that are not neighboring and are placed on opposite sides of the transversal, t.

As a result, our alternate outside angles are:

• ∠5 and ∠9 
• ∠6 and ∠3

Practice Problems on Alternate Exterior Angles

Q1: Given two parallel lines intersected by a transversal, if the measure of ∠1 is 120 degrees, find the measure of the alternate exterior angle, ∠5.

Q2: If ∠A and ∠B are alternate exterior angles, and ∠A measures 50 degrees, what is the measure of ∠B?

Q3: In a pair of parallel lines, if one angle formed by a transversal is 70 degrees, what is the measure of its alternate exterior angle?

Q4: If ∠1 and ∠2 are alternate exterior angles, and ∠1 measures 110 degrees, find the measure of ∠2.

Q5: If the measure of one alternate exterior angle formed by a transversal is 45 degrees, what is the measure of the other alternate exterior angle?

FAQs on Alternate Exterior Angles

What are Alternate Exterior Angles in Math?

Alternate exterior angles are a pair of angles that lie on the opposite sides of a transversal line and on the outer sides of two intersecting lines.

What are the different Types of Alternate Angles?

There are two different types of Alternate Angles. These are called Alternate Interior angles and alternate exterior angles.

What are Alternate Interior and Alternate Exterior Angles?

When two parallel lines are intersected by a transversal, certain angle pairs are formed. One of these pairs is called “alternate interior angles.” These angles are always equal in measure and are found on the inner sides of the parallel lines. Crucially, they are situated on opposite sides of the transversal.

Additionally, there are “alternate exterior angles.” These angles have distinct vertex points, and they are positioned on the alternate sides of the transversal facing outside the parallel lines

How does the Alternate Exterior Angles Theorem work?

When two parallel lines are crossed by a transversal, the exterior angles created on either side of the transversal are equal, according to the alternative exterior angle theorem.

What is the relationship between Alternate Exterior Angles?

When two parallel lines are crossed by a transversal, the alternate exterior angles are regarded congruent angles (identical angles), according to the alternate exterior angle theorem.

What are the differences between Alternate Interior and Alternate Exterior Angles?

When two parallel lines meet at a transversal, they form certain pairs of angles with the transversal. Alternate interior angles are always equal and created on the inner side of parallel lines, but on opposing sides of the transversal.

Outside angles with alternate vertices are positioned on opposite sides of the transversal and are external to the lines.

Are the Opposite Exterior Angles Congruent?

When the lines are parallel, alternate outside angles are congruent. The alternate outside angles are not congruent if the lines are not parallel.

When are the Opposite Exterior Angles Congruent?

Only when two parallel lines crossed by a transversal are alternate exterior angles congruent.