Horje
Rectangle | Definition, Properties, Area, Formula, Examples

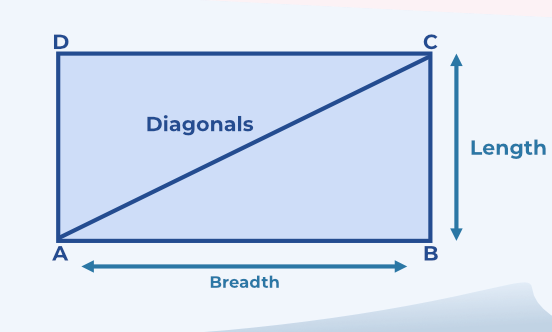
Rectangle is a polygon with four sides, whose all four of its angles are equal to 90 degrees. The opposite sides of a rectangle are both equal in length and run parallel to each other.

Let’s learn about a rectangle, their formulas and their properties in detail.

Table of Content

Rectangle Definition

Rectangle is a closed polygon with four sides in which all four angles are equal and the measure of each angle is 90 degrees. The opposite side of the quadrilateral is parallel and equal.

Shape of Rectangle

A rectangle is a two-dimensional flat shape. The diagram of a rectangle ABCD is shown in the image added below,

Shape of Rectangle

Illustration of a Rectangle

Here, sides AB and CD are equal and parallel and are called the lengths of the rectangle. Also, the sides BC and AD are called the breadth of the rectangle and they are also parallel and equal. AC is the diagonal of the rectangle.

Read More

Length and Breadth of Rectangle

The two sides of the rectangle are classified as the Length and two sides are classified as Breadth.

The longer side of the rectangle is called the length of the rectangle and the shorter side of the rectangle is called the breadth of the rectangle.

From the above image, we have

  • Length of the Rectangle ABCD = AB and CD
  • Breadth of the Rectangle ABCD = BC and DA

The length and the breadth of the rectangle are used to find the Area, Perimeter, and Length of the Diagonal of the Rectangle.

Diagonal of Rectangle

Diagonal of the rectangle is the line connecting the two points of the rectangle by skipping one point.

In Figure 1 the rectangle ABCD has the diagonal AC and its length can be calculated using the Pythagoras Theorem. The diagonal of the rectangle are equal and they bisect each other.

Diagonal of Rectangle Formula

If the length and the breadth of the rectangle are l and b respectively then the diagonal of the rectangle is 

d = √( l2 + b2)

Rectangle Properties

Some of the important properties of a rectangle are:

  • Rectangle is a Polygon with four sides.
  • The angle formed by adjacent sides is 90°.
  • Rectangle is a Quadrilateral.
  • Opposite sides of a Rectangle are Equal and Parallel.
  • Rectangle is considered to be a Parallelogram.
  • Interior Angles of a Rectangle are equal and the value of each angle is 90°.
  • Sum of all Interior Angles is 360°.
  • Diagonals of a Rectangle are equal.
  • Diagonals of a Rectangle bisect each other.
  • Length of the diagonal is found by Pythagoras theorem. If the length and the breadth of the rectangle are l and b respectively then the diagonal of the rectangle is d = √( l2 + b2).

Rectangle Formula

A rectangle is a closed quadrilateral in which the sides are equal and parallel, there are various formulas that are used to find various parameters of the rectangle.

Some of the important formulas of the rectangle are,

  1. Perimeter of Rectangle
  2. Area of Rectangle
Property Formula
Area Length × Breadth
Perimeter 2 × (Length + Breadth)

Let’s discuss them in some detail.

Rectangle Perimeter

Perimeter of the rectangle is defined as the total length of all the sides of the rectangle. It is also called the circumference of the rectangle.

It is measured in units of length, i.e. m, cm, etc.

Perimeter of Rectangle Formula

In a rectangle, if the length(l) and breadth(b) are given then the perimeter of the rectangle is found using the formula,

Perimeter of Rectangle = 2 (l + b)

their

where,

  • l is the length of the rectangle
  • b is the breadth of the rectangle

The figure representing the perimeter of the rectangle is,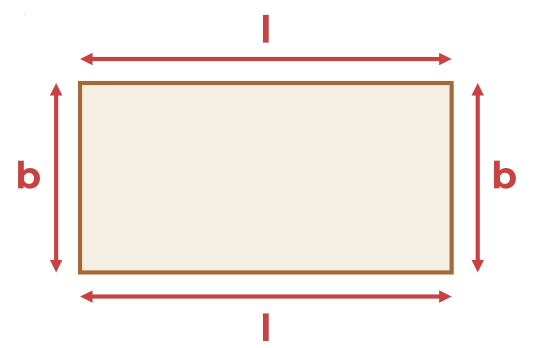

Rectangle Perimeter Formula

Perimeter of Rectangle Illustration

Length of Rectangle Formula

In a rectangle, if the breadth(b) and perimeter(P) are given then its length(l) is found using,

(length) l = (P / 2) – b

In a rectangle, if the breadth(b) and area (A) are given then its length(l) is found using,

(length) l = A/b

Formula for Breadth of Rectangle

In a rectangle, if the length(l) and perimeter(P) are given then its breadth(b) is found using,

(breadth) b = (P / 2) – l

In a rectangle, if the length(l) and area (A) are given then its breadth(b) is found using,

(breadth) b = A/l

Rectangle Area

Area of the rectangle is defined as the total space occupied by the rectangle. It is the space inside the boundary or the perimeter of the rectangle.

The area of the rectangle is dependent on the length and breadth of the rectangle, it is the product of the length and the breadth of the rectangle. The area of a rectangle is measured in square units, i.e. in m2, cm2, etc.

Area of Rectangle Formula

In a rectangle, if the length(l) and breadth(b) are given then the area of the rectangle is found using the formula,

Area of Rectangle = l × b

where,

  • l is the length of the rectangle
  • b is the breadth of the rectangle

Here is a diagram representing the area of the rectangle is,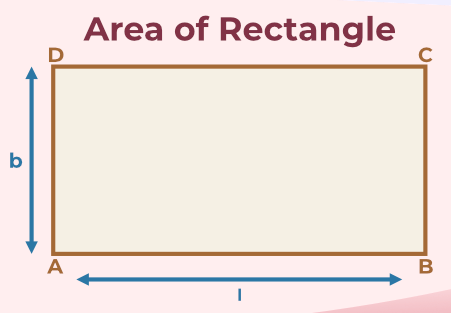

Calculating Rectangle Area

Area of Rectangle Diagram

Types of Rectangle

Rectangles are of two types, which are:

  • Square
  • Golden Rectangle

Let’s learn about them in detail.

Square

A square is a special case of a rectangle in which all the sides are also equal. It is a quadrilateral in which opposite sides are parallel and equal, so it can be considered a rectangle.

The diagram of a square is shown below,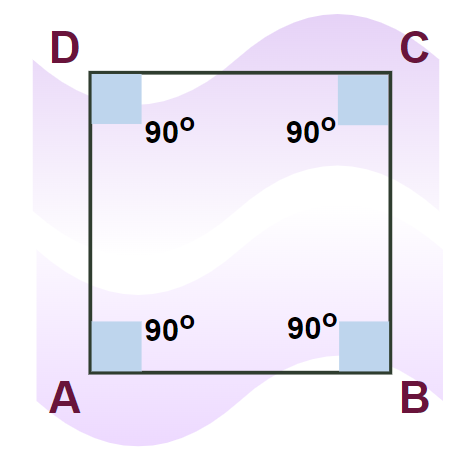

Square Diagram

Diagram of a Square

Learn More

Golden Rectangle

A rectangle in which the ‘length to the width’ ratio is similar to the golden ratio, i.e. equal to the ratio of 1: (1+⎷5)/2 is called the golden rectangle. 

They are in the ratio of 1: 1.618 thus, if its width is 1 m then its length is 1.168 m.

The diagram of a Golden Rectangle is shown below,

Golden Rectangle Diagram

Must Read

Examples on Rectangle

Here are some solved examples on the basic concepts of rectangle for your help.

Example 1: Find the area of the rectangular photo frame whose sides are 8 cm and 6 cm.

Solution:

Given,

  • Length of Photo Frame = 8 cm
  • Breadth of Photo Frame = 6 cm

Area of Photo Frame = Length × Breadth

                                  = 6 × 8 = 48 cm2

Thus, the area of the photo frame is 48 cm2.

Example 2: Find the perimeter of the rectangular field whose sides are 9 m and 13 m.

Solution:

Given,

  • Length of Rectangular Field = 9 m
  • Breadth of Rectangular Field = 13 m

Perimeter of Rectangular Field = 2 × (l + b)

                                                  = 2 × (9 + 13) = 2 × (22)

                                                  = 44 m

Thus, the perimeter of the rectangular field is 44 m.

Example 3: Find the area and the perimeter of the room with a length of 12 feet and a breadth of 8 feet.

Solution:

Given,

  • Length of room (l) = 12 feet
  • Breadth of room (b) = 8 feet

Area of Room = Length × Breadth

                        = 12 × 8 = 96 feet2

Perimeter of Room = 2 × (l + b)

                               = 2 × (12 + 8) = 2 × 20

                               = 40 feet

Thus, the area of the room is 96 feet2, and the perimeter is 40 feet.

Example 4: Find the length of the diagonal of the rectangle whose sides are 6 cm and 8 cm.

Solution:

Given,

  • Length of rectangle (l) = 6 cm
  • Breadth of rectangle (b) = 8 cm

Length of diagonal (d) = √( l2 + b2)

d = √( 82 + 62) 

d = √ (64 + 36) = √(100)

d = 10 cm

Thus, the length of the rectangle is 10 cm

Rectangle – FAQs

What is Rectangle in Geometry?

A rectangle is a quadrilateral in which all the angles are equal and the opposite sides are parallel and equal. Thus, a rectangle is a special quadrilateral also square also comes under the category of a rectangle.

What are the properties of rectangle?

Various properties of a rectangle are,

  • All the angles of the rectangle are equal.
  • Opposite sides of the rectangle are equal and parallel.
  • Diagonals of the rectangle bisect each other.

What is Formula of Area of Rectangle?

Formula for calculating the area of the rectangle is,

Area of a Rectangle = (l × b)

What is Formula of Perimeter of a Rectangle?

Formula for calculating the perimeter of the rectangle is,

Perimeter of a Rectangle = 2(l + b)

What is Formula of Diagonal of Rectangle?

Formula for calculating the diagonal of the rectangle is,

Diagonal of a Rectangle = √( l2 + b2)

What is Formula of Length of Rectangle?

Formula for calculating the length of the rectangle is,

Length = Perimeter/2 – Breadth

What is Formula of Breadth of Rectangle?

Formula for calculating the breadth of the rectangle is,

Breadth = Perimeter/2 – Length

Can Rectangle be a Square?

Yes, rectangle can be a square, if adjacent sides of rectangle are equal then it is a square.

Can Rectangle be a Rhombus?

Yes, rectangle can be a rhombus, if adjacent sides of rectangle are equal then it is a square as well rhombus.

What is the shape of rectangle?

A rectangle is a two-dimensional flat shape. It is a four-sided polygon, known as a quadrilateral.


 


Reffered: https://www.geeksforgeeks.org

Mathematics

Related
13 Times Table | Learn Multiplication Table of Thirteen 13 Times Table | Learn Multiplication Table of Thirteen
Learn Multiplication Table of Twelve | 12 Times Table Learn Multiplication Table of Twelve | 12 Times Table
Table 1 to 20: Table from 1 to 20 PDF Table 1 to 20: Table from 1 to 20 PDF
15 Times Table | Learn Multiplication Table of Fifteen 15 Times Table | Learn Multiplication Table of Fifteen
Differentiation Formulas | Trigonometric, Inverse Trig, Hyperbolic Formulas Differentiation Formulas | Trigonometric, Inverse Trig, Hyperbolic Formulas

Type:
 Geek
Category:
 Coding
Sub Category:
 Tutorial
Uploaded by:
 Admin
Views:
 12



 

Horje