|
Given an undirected graph consisting of N nodes labeled from 0 to N – 1, which are represented by a 2D array arr[][], where arr[i] represents all the nodes that are connected to the ith node, the task is to find whether we can visit all the nodes from node X.
Examples:
Input: arr = { { 1, 2 }, { 0, 3, 2 }, {0, 1}, {1} }, N = 4, X = 0
Output: YES
Explanation: As can be seen from the below graph, we can reach to any node from node 0.
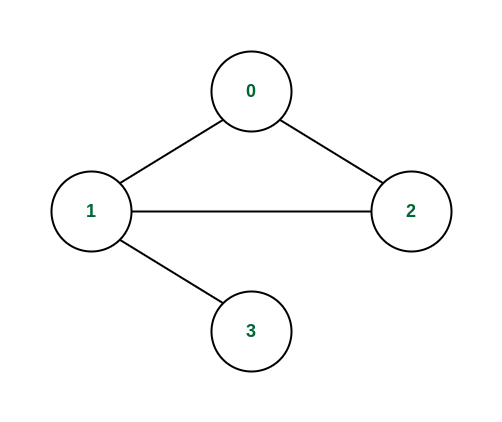 The structure of the above graph Input: arr = { { 1, 2 }, { 0, 3, 2 }, {0, 1}, {1} }, N = 5, X = 4
Output: NO
Explanation: No node is connected to the node 4.
An approach using BFS:The idea is to use BFS from starting from node X and count all the nodes that are visited in the path. Finally check if number of nodes that are visited are equal to given number of node N or not. If they are equal then print YES, otherwise NO.
We mainly maintain a count variable along with the standard BFS starting from X. If count of visited nodes becomes equal to to number of nodes in the graph at the end, we say all nodes are reachable, otherwise not.
C++
// C++ code for the above approach:
#include <bits/stdc++.h>
using namespace std;
// Function to find if
// all nodes can be visited from X
bool canVisitAllNodes(vector<vector<int> >& arr,
int X, int n)
{
// Standard BFS code with an extra count
// variable
queue<int> q;
vector<int> visited(n, false);
q.push(X);
visited[X] = true;
int count = 0;
while (q.size() > 0) {
auto curr = q.front();
cout << curr << endl;
q.pop();
count++;
for (auto j : arr[curr]) {
if (visited[j] == false) {
q.push(j);
visited[j] = true;
}
}
}
// Check if all nodes are visited
if (count == n)
return true;
return false;
}
// Driver code
int main()
{
vector<vector<int> > arr
= { { 1, 2 }, { 0, 3, 2 }, { 0, 1 }, { 1 } };
int N = 4, X = 0;
// Function Call
if (canVisitAllNodes(arr, X, N)) {
cout << "YES" << endl;
}
else {
cout << "NO" << endl;
}
return 0;
}
// Java code for the above approach:
import java.io.*;
import java.util.*;
class GFG {
// Function to find if all nodes can be visited from X
static boolean canVisitAllNodes(int[][] arr, int X,
int n)
{
Queue<Integer> q = new LinkedList<>();
boolean[] visited = new boolean[n];
Arrays.fill(visited, Boolean.FALSE);
q.add(X);
visited[X] = true;
int count = 0;
// Loop to implement BFS
while (q.size() > 0) {
int size = q.size();
for (int i = 0; i < size; i++) {
int curr = q.poll();
count++;
for (var j : arr[curr]) {
if (visited[j] == false) {
q.add(j);
visited[j] = true;
}
}
}
}
// Check if all nodes are visited
if (count == n) {
return true;
}
return false;
}
public static void main(String[] args)
{
int[][] arr
= { { 1, 2 }, { 0, 3, 2 }, { 0, 1 }, { 1 } };
int N = 4, X = 0;
// Function call
if (canVisitAllNodes(arr, X, N)) {
System.out.println("YES");
}
else {
System.out.println("NO");
}
}
}
// This code is contributed by lokeshmvs21.
# Python code for the above approach:
# Function to find if
# all nodes can be visited from X
def canVisitAllNodes(arr, X, n):
q = []
visited = [False]*n
q.append(X)
visited[X] = True
count = 0
# Loop to implement BFS
while(len(q) > 0):
size = len(q)
for i in range(size):
curr = q.pop(0)
count = count + 1
for j in arr[curr]:
if(visited[j] == False):
q.append(j)
visited[j] = True
# Check if all nodes are visited
if(count == n):
return True
return False
# Driver code
arr = [[1, 2], [0, 3, 2], [0, 1], [1]]
N, X = 4, 0
# Function Call
if(canVisitAllNodes(arr, X, N)):
print("YES")
else:
print("NO")
# This code is contributed by Pushpesh Raj.
// C# code to implement the approach
using System;
using System.Collections.Generic;
public class GFG {
// Driver Code
public static void Main(string[] args)
{
int[][] arr = new int[4][];
arr[0] = new int[] { 1, 2 };
arr[1] = new int[] { 0, 3, 2 };
arr[2] = new int[] { 0, 1 };
arr[3] = new int[] { 1 };
int n = 4, X = 0;
Queue<int> q = new Queue<int>();
bool[] visited = new bool[n];
for (int i = 0; i < n; i++) {
visited[i] = false;
}
q.Enqueue(X);
visited[X] = true;
int count = 0;
// Loop to implement BFS
while (q.Count > 0) {
int size = q.Count;
for (int i = 0; i < size; i++) {
int curr = q.Dequeue();
count++;
for (int k = 0; k < arr[curr].Length; k++) {
int j = arr[curr][k];
if (visited[j] == false) {
q.Enqueue(j);
visited[j] = true;
}
}
}
}
// Check if all nodes are visited
if (count == n) {
Console.Write("Yes");
}
else {
Console.Write("NO");
}
}
}
// This code is contributed by garg28harsh.
// Javascript code for the above approach:
// Function to find if
// all nodes can be visited from X
function canVisitAllNodes(arr, X, n) {
let q = [];
let visited = new Array(n).fill(false);
q.push(X);
visited[X] = true;
let count = 0;
// Loop to implement BFS
while (q.length > 0) {
let size = q.length;
for (let i = 0; i < size; i++) {
let curr = q.shift();
count++;
for (let j of arr[curr]) {
if (visited[j] == false) {
q.push(j);
visited[j] = true;
}
}
}
}
// Check if all nodes are visited
if (count == n)
return true;
return false;
}
// Driver code
var arr = [ [ 1, 2 ], [ 0, 3, 2 ], [ 0, 1 ], [ 1 ] ];
var N = 4, X = 0;
// Function Call
if (canVisitAllNodes(arr, X, N)) {
console.log("YES");
}
else {
console.log("NO");
}
// This code is contributed by Tapesh(tapeshdua420)
Time Complexity: O(N + E) where N is the number of nodes and E is the number of edges.
Auxiliary Space: O(N)
|
