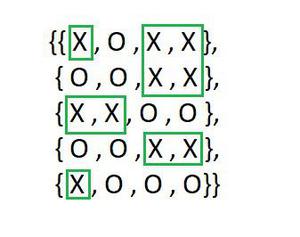Horje
Count submatrices having only 'X' in given Matrix

Given a character matrix consisting of O’s and X’s, find the number of submatrices containing only ‘X’ and surrounded by ‘O’ from all sides. 

Examples:

Input:  grid[][] = {{X, O, X}, {O, X, O}, {X, X, X}}
Output: 3

Input: grid[][] = { { ‘X’, ‘O’, ‘X’, ‘X’ }, { ‘O’, ‘O’, ‘X’, ‘X’ }, { ‘X’, ‘X’, ‘O’, ‘O’ }, { ‘O’, ‘O’, ‘X’, ‘X’ }, { ‘X’, ‘O’, ‘O’, ‘O’ } };
Output: 5
Explanation: See the image below for understanding

Image of the above matrix

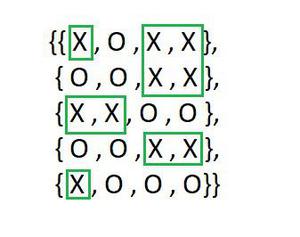Image of the above matrix

Submatrices containing X using DFS:

Follow the below idea to solve the problem:

Run a dfs for each X and find the submatrix whose part it is.

Below are the steps to solve the problem:

  •  Initialize a 2D array (say visited[][]) having the size same as the given matrix just to keep track of the visited cell in the given matrix.
  •  Perform the DFS Traversal on the unvisited cell having the value ‘X’ in the given matrix 
    • Then mark this cell as visited and recursively call DFS for all four directions i.e right, left, up, and down to make all the connected ‘X’ as visited and count this connected ‘X’ shape in the resultant count.
  • Repeat the above steps until all the cells having value ‘X’ are not visited.

Below is the implementation of the above approach.

C++

// C++ code to implement the approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to check if it is valid
// to move on the next cell
bool isValid(int row, int col, vector<vector<char> >& grid,
             vector<vector<int> >& visited)
{
    return (row < grid.size()) && (row >= 0)
           && (col < grid[0].size()) && (col >= 0)
           && (grid[row][col] == 'X')
           && (visited[row][col] == 0);
}
 
// Function to implement dfs
void dfs(int row, int col, vector<vector<char> >& grid,
         vector<vector<int> >& visited)
{
    if (!isValid(row, col, grid, visited))
        return;
    visited[row][col] = 1;
    dfs(row + 1, col, grid, visited);
    dfs(row, col + 1, grid, visited);
    dfs(row - 1, col, grid, visited);
    dfs(row, col - 1, grid, visited);
}
 
// Function to count the total number of submatrices
int xShape(vector<vector<char> >& grid)
{
    int n = grid.size();
    int m = grid[0].size();
    vector<vector<int> > visited(n, vector<int>(m, 0));
    int count = 0;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (visited[i][j] == 0 and grid[i][j] == 'X') {
                dfs(i, j, grid, visited);
                count++;
            }
        }
    }
    return count;
}
 
// Driver code
int main()
{
    vector<vector<char> > grid{ { 'X', 'O', 'X', 'X' },
                                { 'O', 'O', 'X', 'X' },
                                { 'X', 'X', 'O', 'O' },
                                { 'O', 'O', 'X', 'X' },
                                { 'X', 'O', 'O', 'O' } };
 
    // Function Call
    cout << xShape(grid);
    return 0;
}

Java

// Java Code to implement above approach
import java.util.*;
 
public class Solution {
 
  // Function to check if it is valid
  // to move on the next cell
  static boolean isValid(int row, int col, char[][] grid,
                         int[][] visited)
  {
    return (row < grid.length) && (row >= 0)
      && (col < grid[0].length) && (col >= 0)
      && (grid[row][col] == 'X')
      && (visited[row][col] == 0);
  }
 
  // Function to implement dfs
  static void dfs(int row, int col, char[][] grid,
                  int[][] visited)
  {
    if (!isValid(row, col, grid, visited))
      return;
    visited[row][col] = 1;
    dfs(row + 1, col, grid, visited);
    dfs(row, col + 1, grid, visited);
    dfs(row - 1, col, grid, visited);
    dfs(row, col - 1, grid, visited);
  }
 
  // Function to count the total number of submatrices
  static int xShape(char[][] grid)
  {
    int n = grid.length;
    int m = grid[0].length;
    int[][] visited = new int[n][m];
    int count = 0;
    for (int i = 0; i < n; i++) {
      for (int j = 0; j < m; j++) {
        if (visited[i][j] == 0
            && grid[i][j] == 'X') {
          dfs(i, j, grid, visited);
          count++;
        }
      }
    }
    return count;
  }
 
  // Driver code
  public static void main(String[] args)
  {
    char[][] grid = { { 'X', 'O', 'X', 'X' },
                     { 'O', 'O', 'X', 'X' },
                     { 'X', 'X', 'O', 'O' },
                     { 'O', 'O', 'X', 'X' },
                     { 'X', 'O', 'O', 'O' } };
    System.out.println(xShape(grid));
  }
}
 
// This code is contributed by karandeep1234

Python3

# Function to check if it is valid
# to move on the next cell
def is_valid(row, col, grid, visited):
    return (row < len(grid)) and (row >= 0) and (col < len(grid[0])) and (col >= 0) and (grid[row][col] == 'X') and (visited[row][col] == 0)
 
# Function to implement dfs
def dfs(row, col, grid, visited):
    if not is_valid(row, col, grid, visited):
        return
    visited[row][col] = 1
    dfs(row + 1, col, grid, visited)
    dfs(row, col + 1, grid, visited)
    dfs(row - 1, col, grid, visited)
    dfs(row, col - 1, grid, visited)
 
# Function to count the total number of submatrices
def x_shape(grid):
    n = len(grid)
    m = len(grid[0])
    visited = [[0 for _ in range(m)] for _ in range(n)]
    count = 0
    for i in range(n):
        for j in range(m):
            if visited[i][j] == 0 and grid[i][j] == 'X':
                dfs(i, j, grid, visited)
                count += 1
    return count
 
grid = [
    ['X', 'O', 'X', 'X'],
    ['O', 'O', 'X', 'X'],
    ['X', 'X', 'O', 'O'],
    ['O', 'O', 'X', 'X'],
    ['X', 'O', 'O', 'O']
]
 
#Function call
print(x_shape(grid))
 
# contributed by akashish__

C#

// C# Code to implement above approach
using System;
 
public class Solution {
 
  // Function to check if it is valid
  // to move on the next cell
  static bool isValid(int row, int col, char[, ] grid,
                      int[, ] visited)
  {
    return (row < grid.GetLength(0)) && (row >= 0)
      && (col < grid.GetLength(1)) && (col >= 0)
      && (grid[row, col] == 'X')
      && (visited[row, col] == 0);
  }
 
  // Function to implement dfs
  static void dfs(int row, int col, char[, ] grid,
                  int[, ] visited)
  {
    if (!isValid(row, col, grid, visited))
      return;
    visited[row, col] = 1;
    dfs(row + 1, col, grid, visited);
    dfs(row, col + 1, grid, visited);
    dfs(row - 1, col, grid, visited);
    dfs(row, col - 1, grid, visited);
  }
 
  // Function to count the total number of submatrices
  static int xShape(char[, ] grid)
  {
    int n = grid.GetLength(0);
    int m = grid.GetLength(1);
    int[, ] visited = new int[n, m];
    int count = 0;
    for (int i = 0; i < n; i++) {
      for (int j = 0; j < m; j++) {
        if (visited[i, j] == 0
            && grid[i, j] == 'X') {
          dfs(i, j, grid, visited);
          count++;
        }
      }
    }
    return count;
  }
 
  // Driver code
  public static void Main(string[] args)
  {
    char[, ] grid
      = new char[, ] { { 'X', 'O', 'X', 'X' },
                      { 'O', 'O', 'X', 'X' },
                      { 'X', 'X', 'O', 'O' },
                      { 'O', 'O', 'X', 'X' },
                      { 'X', 'O', 'O', 'O' } };
    Console.WriteLine(xShape(grid));
  }
}
 
// This code is contributed by karandeep1234

Javascript

<script>
       // JavaScript code for the above approach
 
       // Function to check if it is valid
       // to move on the next cell
       function isValid(row, col, grid,
           visited) {
           return (row < grid.length) && (row >= 0)
               && (col < grid[0].length) && (col >= 0)
               && (grid[row][col] == 'X')
               && (visited[row][col] == 0);
       }
 
       // Function to implement dfs
       function dfs(row, col, grid,
           visited) {
           if (!isValid(row, col, grid, visited))
               return;
           visited[row][col] = 1;
           dfs(row + 1, col, grid, visited);
           dfs(row, col + 1, grid, visited);
           dfs(row - 1, col, grid, visited);
           dfs(row, col - 1, grid, visited);
       }
 
       // Function to count the total number of submatrices
       function xShape(grid) {
           let n = grid.length;
           let m = grid[0].length;
           let visited = new Array(n);
           for (let i = 0; i < n; i++) {
               visited[i] = new Array(m).fill(0);
           }
           let count = 0;
           for (let i = 0; i < n; i++) {
               for (let j = 0; j < m; j++) {
                   if (visited[i][j] == 0 && grid[i][j] == 'X') {
                       dfs(i, j, grid, visited);
                       count++;
                   }
               }
           }
           return count;
       }
 
       // Driver code
       let grid = [['X', 'O', 'X', 'X'],
       ['O', 'O', 'X', 'X'],
       ['X', 'X', 'O', 'O'],
       ['O', 'O', 'X', 'X'],
       ['X', 'O', 'O', 'O']];
 
       // Function Call
       document.write(xShape(grid));
 
// This code is contributed by Potta Lokesh
   </script>

Output

5

Time Complexity: O(ROW x COL)
Auxiliary Space: O(ROW x COL), where ROW = Number of rows in the given grid, COL = Number of columns in the given grid. 

Space Optimized approach for finding Submatrices containing X: 

In the above method, we are using an extra space i.e the visited[ ][ ] array in order to keep track of the visited cell. Alternatively, We can do this without using the Auxiliary space but for that, we have to change the given matrix.

Below are the steps to solve the problem:

  • Just Perform the DFS Traversal on the cell having the value ‘X’ in the given matrix then change the value of that cell to ‘O’ so that it will not visit it again and 
  • Recursively call DFS in all the four directions i.e right, left, up and down to change all the connected ‘X’ to ‘O’ and count this connected ‘X’ shape in the resultant count.
  • Repeat the above steps until all the ‘X’ in the given matrix are not changed to ‘O’.

Below is the implementation for the above approach.

C++

// C++ code to implement the approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to check if it is valid
// to traverse the next cell
bool isValid(int row, int col, vector<vector<char> >& grid)
{
    return (row < grid.size()) && (row >= 0)
           && (col < grid[0].size()) && (col >= 0)
           && (grid[row][col] == 'X');
}
 
// Function to implement dfs
void dfs(int row, int col, vector<vector<char> >& grid)
{
    if (!isValid(row, col, grid))
        return;
    grid[row][col] = 'O';
    dfs(row + 1, col, grid);
    dfs(row, col + 1, grid);
    dfs(row - 1, col, grid);
    dfs(row, col - 1, grid);
}
 
// Function to count the submatrices
int xShape(vector<vector<char> >& grid)
{
    // Code here
    int n = grid.size();
    int m = grid[0].size();
    int count = 0;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (grid[i][j] == 'X') {
                dfs(i, j, grid);
                count++;
            }
        }
    }
    return count;
}
 
// Driver code
int main()
{
    vector<vector<char> > grid{ { 'X', 'O', 'X', 'X' },
                                { 'O', 'O', 'X', 'X' },
                                { 'X', 'X', 'O', 'O' },
                                { 'O', 'O', 'X', 'X' },
                                { 'X', 'O', 'O', 'O' } };
 
    // Function Call
    cout << xShape(grid);
 
    return 0;
}

Java

/*package whatever //do not write package name here */
import java.io.*;
 
class GFG {
 
  // Function to check if it is valid
  // to traverse the next cell
  static boolean isValid(int row, int col, char[][] grid)
  {
    return (row < grid.length) && (row >= 0)
      && (col < grid[0].length) && (col >= 0)
      && (grid[row][col] == 'X');
  }
 
  // Function to implement dfs
  static void dfs(int row, int col, char[][] grid)
  {
    if (!isValid(row, col, grid))
      return;
    grid[row][col] = 'O';
    dfs(row + 1, col, grid);
    dfs(row, col + 1, grid);
    dfs(row - 1, col, grid);
    dfs(row, col - 1, grid);
  }
 
  // Function to count the submatrices
  static int xShape(char[][] grid)
  {
    // Code here
    int n = grid.length;
    int m = grid[0].length;
    int count = 0;
    for (int i = 0; i < n; i++) {
      for (int j = 0; j < m; j++) {
        if (grid[i][j] == 'X') {
          dfs(i, j, grid);
          count++;
        }
      }
    }
    return count;
  }
 
  public static void main(String[] args)
  {
    char[][] grid = { { 'X', 'O', 'X', 'X' },
                     { 'O', 'O', 'X', 'X' },
                     { 'X', 'X', 'O', 'O' },
                     { 'O', 'O', 'X', 'X' },
                     { 'X', 'O', 'O', 'O' } };
 
    // Function Call
    System.out.println(xShape(grid));
  }
}
 
// This code is contributed by aadityaburujwale.

Python3

class GFG :
    # Function to check if it is valid
    # to traverse the next cell
    @staticmethod
    def  isValid( row,  col,  grid) :
        return (row < len(grid)) and (row >= 0) and (col < len(grid[0])) and (col >= 0) and (grid[row][col] == 'X')
     
    # Function to implement dfs
    @staticmethod
    def dfs( row,  col,  grid) :
        if (not GFG.isValid(row, col, grid)) :
            return
        grid[row][col] = 'O'
        GFG.dfs(row + 1, col, grid)
        GFG.dfs(row, col + 1, grid)
        GFG.dfs(row - 1, col, grid)
        GFG.dfs(row, col - 1, grid)
         
    # Function to count the submatrices
    @staticmethod
    def  xShape( grid) :
       
        # Code here
        n = len(grid)
        m = len(grid[0])
        count = 0
        i = 0
        while (i < n) :
            j = 0
            while (j < m) :
                if (grid[i][j] == 'X') :
                    GFG.dfs(i, j, grid)
                    count += 1
                j += 1
            i += 1
        return count
    @staticmethod
    def main( args) :
        grid = [['X', 'O', 'X', 'X'], ['O', 'O', 'X', 'X'], ['X', 'X', 'O', 'O'], ['O', 'O', 'X', 'X'], ['X', 'O', 'O', 'O']]
         
        # Function Call
        print(GFG.xShape(grid))
     
 
if __name__=="__main__":
    GFG.main([])
     
    # This code is contributed by aadityaburujwale.

Javascript

<script>
       // JavaScript code for the above approach
 
       // Function to check if it is valid
       // to move on the next cell
       function isValid(row, col, grid,
           visited) {
           return (row < grid.length) && (row >= 0)
               && (col < grid[0].length) && (col >= 0)
               && (grid[row][col] == 'X')
               && (visited[row][col] == 0);
       }
 
       // Function to implement dfs
       function dfs(row, col, grid,
           visited) {
           if (!isValid(row, col, grid, visited))
               return;
           visited[row][col] = 1;
           dfs(row + 1, col, grid, visited);
           dfs(row, col + 1, grid, visited);
           dfs(row - 1, col, grid, visited);
           dfs(row, col - 1, grid, visited);
       }
 
       // Function to count the total number of submatrices
       function xShape(grid) {
           let n = grid.length;
           let m = grid[0].length;
           let visited = new Array(n);
           for (let i = 0; i < n; i++) {
               visited[i] = new Array(m).fill(0);
           }
           let count = 0;
           for (let i = 0; i < n; i++) {
               for (let j = 0; j < m; j++) {
                   if (visited[i][j] == 0 && grid[i][j] == 'X') {
                       dfs(i, j, grid, visited);
                       count++;
                   }
               }
           }
           return count;
       }
 
       // Driver code
       let grid = [['X', 'O', 'X', 'X'],
       ['O', 'O', 'X', 'X'],
       ['X', 'X', 'O', 'O'],
       ['O', 'O', 'X', 'X'],
       ['X', 'O', 'O', 'O']];
 
       // Function Call
       document.write(xShape(grid));
 
// This code is contributed by Potta Lokesh
 
   </script>

C#

// C# code to implement the approach
 
using System;
 
public class GFG {
 
    // Function to check if it is valid
    // to traverse the next cell
    static bool isValid(int row, int col, char[, ] grid)
    {
        return (row < grid.GetLength(0)) && (row >= 0)
            && (col < grid.GetLength(1)) && (col >= 0)
            && (grid[row, col] == 'X');
    }
 
    // Function to implement dfs
    static void dfs(int row, int col, char[, ] grid)
    {
        if (!isValid(row, col, grid))
            return;
        grid[row, col] = 'O';
        dfs(row + 1, col, grid);
        dfs(row, col + 1, grid);
        dfs(row - 1, col, grid);
        dfs(row, col - 1, grid);
    }
 
    // Function to count the submatrices
    static int xShape(char[, ] grid)
    {
        // Code here
        int n = grid.GetLength(0);
        int m = grid.GetLength(1);
        int count = 0;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (grid[i, j] == 'X') {
                    dfs(i, j, grid);
                    count++;
                }
            }
        }
        return count;
    }
 
    static public void Main()
    {
 
        // Code
        char[, ] grid = { { 'X', 'O', 'X', 'X' },
                          { 'O', 'O', 'X', 'X' },
                          { 'X', 'X', 'O', 'O' },
                          { 'O', 'O', 'X', 'X' },
                          { 'X', 'O', 'O', 'O' } };
 
        // Function Call
        Console.WriteLine(xShape(grid));
    }
}
 
// This code is contributed by lokeshmvs21.

Output

5

Time Complexity: O(ROW x COL)
Auxiliary Space: O(1)


 


Reffered: https://www.geeksforgeeks.org

Data Structures

Related
Sort an Array of Strings in Lexicographical order Sort an Array of Strings in Lexicographical order
Differences between Array and Dictionary Data Structure Differences between Array and Dictionary Data Structure
Count of Pairs with given sum in Rotated Sorted Array Count of Pairs with given sum in Rotated Sorted Array
Allocate minimum number of pages (Non Consecutive) Allocate minimum number of pages (Non Consecutive)
Find 132 Pattern from given Array Find 132 Pattern from given Array

Type:
 Geek
Category:
 Coding
Sub Category:
 Tutorial
Uploaded by:
 Admin
Views:
 14



 

Horje