Pyramid is a three-dimensional geometric structure with a polygonal base and triangular faces equal to the number of sides in the base. The triangular faces or lateral surfaces of a pyramid meet at a single point known as the apex or the vertex.

Surface Area of a Square Pyramid

In a pyramid, the base is connected to all the faces of the pyramid. Pyramids are classified into different types, such as triangular pyramids, square pyramids, rectangular pyramids, pentagonal pyramids, hexagonal pyramid, etc., based on the shape of the polygonal base.

Square Pyramid

A square pyramid is a pyramid that has a square base and four triangular faces that meet at a point at the top called the apex. The Great Pyramid of Giza and the Hipped roofs are the best examples of a square pyramid. A square pyramid is also referred to as a pentahedron as it has five faces, including a square base and four triangular faces (lateral faces). It has a total of 5 faces, 4 triangular faces, a square base, 5 vertices, and 8 edges.

There are various types of square pyramids, such as equilateral square pyramids, right square pyramids, and oblique square pyramids, based on the length of their edges, alignment of the apex, etc.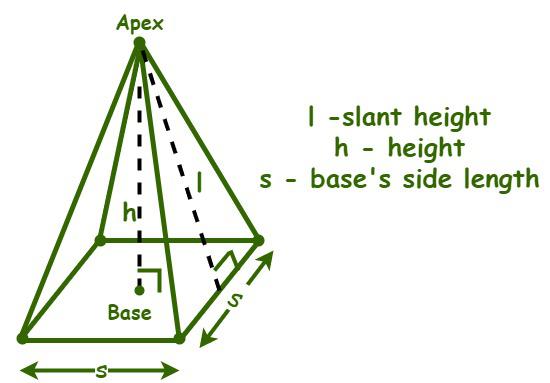

Surface Area of a Square Pyramid

Surface Area of a Square Pyramid

The term “surface” refers to “the exterior part of an object or a body”. “Surface area” means the total region occupied by the surfaces of a three-dimensional object. Hence, the total surface area of a square pyramid is the sum of the areas of its lateral faces and its base area. A pyramid has two kinds of surface areas: the lateral surface area and the total surface area. The lateral surface area of a pyramid is the area occupied by its lateral surfaces or side faces.

Surface Area of a Square Pyramid

Lateral surface area of a square pyramid

The lateral surface area of a pyramid is the area occupied by its lateral surfaces or side faces. The formula for calculating the lateral surface area of a square pyramid using slant height is given as follows,

Lateral surface area (LSA) = ½ × perimeter × slant height

We know that,

The perimeter of a square = 4s

So, LSA = ½ × 4s × l = 2sl

Lateral surface area of a square pyramid (LSA) = 2sl square units

Where,

“s” is the base length of a square pyramid,

“l” is the slant height or height of each side face.

The slant height of the pyramid (l) = √(s²/4 + h²)

The formula for calculating the lateral surface area of a square pyramid using the height is given as follows,

Lateral surface area of a square pyramid = 2s√(s²/4 + h2) square units

where,

“s” is the base length of a square pyramid,

“h” is the height of the square pyramid.

Total surface area of a square pyramid

The total surface area of a square pyramid is the sum of the areas of its lateral faces and its base area. The formula for calculating the total  surface area of a square pyramid is given as follows,

Total surface area of a pyramid (TSA) = Lateral surface area of the pyramid (LSA) + Base area

The lateral surface area of the square pyramid (LSA)= 2sl square units

Base area = s² square units

So, TSA = 2sl + s²

Total surface area of a square pyramid (TSA) = 2sl + s²  square units

where,

 “s” is the base length of a square pyramid,

“l” is the slant height or height of each side face.

Slant height of the pyramid (l) = √(s²/4 + h²)

The formula for calculating the lateral surface area of a square pyramid using the height is given as follows,

Total surface area of a square pyramid (TSA) = 2s√(s²/4 + h²) + s²  square units

where,

“s” is the base length of a square pyramid,

“h” is the height of the square pyramid.

Solved Examples on Square Pyramid Formulas

Example 1: Determine the total surface area of a square pyramid if the base’s side length is 15 cm and the pyramid’s slant height is 21 cm.

Solution:

Given,

The side of the square base (s) = 15 cm

Slant height, (l) = 21 cm

The perimeter of the square base (P) = 4s = 4(15) = 60 cm

The lateral surface area of a square pyramid = (½) Pl

LSA = (½ ) × (60) × 21 = 630 sq. cm

Now, the total surface area = Area of the base + LSA

= s² + LSA

= (15)² + 630

= 225 + 630 = 855 sq. cm

Therefore, the total surface area of the given pyramid is 855 sq. cm.

Example 2: Determine the lateral surface area of a square pyramid if the side length of the base is 18 inches and the pyramid’s slant height is 22 inches.

Solution:

Given,

The side of the square base (s) = 18 inches

Slant height, (l) = 22 inches

The perimeter of the square base (P) = 4s = 4(18) = 72 inches

The lateral surface area of a square pyramid = (½) Pl

LSA = (½ ) × (72) × 22 = 792 sq. in.

Therefore, the lateral surface area of the given pyramid is 792 sq. in.

Example 3: What is the slant height of the square pyramid if its lateral surface area is 200 sq. in. and the side length of the base is 10 inches?

Solution:

Given data,

Length of the side of the base of a square pyramid (s) = 10 inches

The lateral surface area of a square pyramid = 200 sq. in

Slant height (l) = ?

We know that,

The lateral surface area of a square pyramid = (½) Pl

The perimeter of the square base (P) = 4s = 4(10) = 40 inches

⇒ 200 = ½ × 40 × l

⇒ l = 10 in

Hence, the slant height of the square pyramid is 10 inches.

Example 4: Calculate the side length of the base of the square pyramid if its lateral surface area is 480 sq. cm and the slant height is 24 cm.

Solution:

Given data,

The lateral surface area of a square pyramid = 480 sq. cm

Slant height (l) = 24 cm

Let the length of the side of the base of a square pyramid be “s”.

We know that,

The lateral surface area of a square pyramid = (½) Pl

The perimeter of the square base (P) = 4s

⇒ 480 = ½ × 4s × 24

⇒ s = 10 cm

Hence, the side length of the base of the square pyramid is 10 cm.

Example 5: Determine the total surface area of a square pyramid if the base’s side length is 14 cm and the pyramid’s height is 24 cm.

Solution:

Given,

The side of the square base (s) = 14 cm

The height of the square pyramid (h) = 24 cm

The slant height of the pyramid (l) = √[(s/2)² + h²]

l = √[(14/2)² + 24²)] = √(49+576)

= √625 = 25 cm

The perimeter of the square base (P) = 4s = 4(14) = 56 cm

The lateral surface area of a square pyramid = (½) Pl

LSA = (½ ) × (56) × 25 = 700‬ sq. cm

Now, the total surface area = Area of the base + LSA

= s² + LSA

= (14)² + 700‬

= 196 + 700‬ = 896 sq. cm

Therefore, the total surface area of the given pyramid is 896 sq. cm.

Example 6: Determine the surface area of a square pyramid if the base’s side length is 10 cm and the pyramid’s slant height is 15 cm.

Solution:

Given,

The side of the square base (s) = 10 cm

Slant height (l) = 15 cm

We know that,

The total surface area of a square pyramid (TSA) = 2sl + s²  square units

= 2 × 10 × 15 + (10)²

= 300 + 100 = 400 sq. cm

Therefore, the surface area of the given pyramid is 400 sq. cm.

Surface Area of a Square Pyramid – FAQs

What is the area of the base of a Square Pyramid?

Base of a square pyramid is shaped as square. Thus, the area of the base of square pyramid can be calculated using the formula, for area of square.

Area of base Square Pyramid = a²,

where,

a is the length of the base of the square pyramid.

How many bases does a Square Pyramid have?

A square pyramid is a pyramid with only one base in shape of a square. So, a square pyramid has only one base.

Which two shapes make up a Square Pyramid?

The base of a square pyramid is a square and all its side faces are triangles. So there are two shapes that make up a square pyramid which are square and triangle.

What is the area of one of the triangular faces of a Square Pyramid?

Suppose, a is the length of base and l is the slant height of a square pyramid, then the area of any one of the four triangular side faces is, 

Area = ½ × a × l.