|
|
A Hyperbola is a smooth curve in a plane with two branches that mirror each other, resembling two infinite bows. It is a conic section formed by intersecting a right circular cone with a plane at an angle such that both halves of the cone are intersected. Let’s learn about Hyperbola in detail, including its Equation, Formulas, Properties, Graphs, and Derivation.  Hyperbola Table of Content
What is Hyperbola?A hyperbola is the locus of points whose difference in the distances from two foci is a fixed value. This difference is obtained by subtracting the distance of the nearer focus from the distance of the farther focus. If P (x, y) is a point on the hyperbola and F, F’ are two foci, then the locus of the hyperbola is
Note: Refer diagram added in derivation for image. Hyperbola Definition
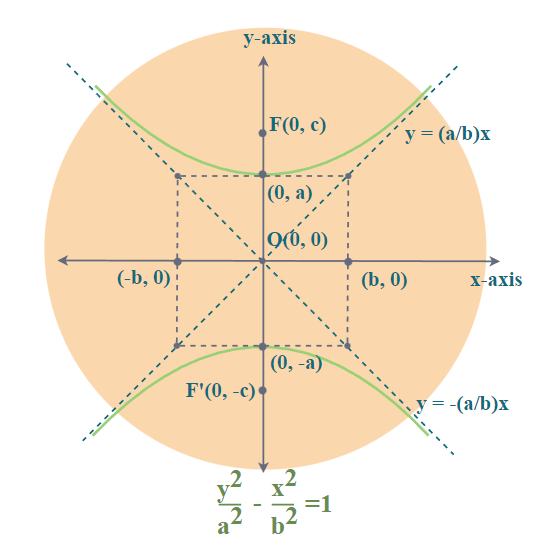
Hyperbola EquationThe equation of a hyperbola in its standard form depends on its orientation and whether it’s centered at the origin or another point. Here are the two primary forms for hyperbolas centered at the origin, one opening horizontally and the other opening vertically:
This equation represents a hyperbola that opens to the left and right. The points (±a,0) are the vertices of the hyperbola, located on the x-axis. Parts of HyperbolaA hyperbola is a conic section that is developed when a plane cuts a double right circular cone at an angle such that both halves of the cone are joined. It can be described using concepts like foci, directrix, latus rectum, and eccentricity.
Hyperbola EccentricityThe eccentricity of a hyperbola is the ratio of the distance of a point from the focus to its perpendicular distance from the directrix. It is denoted by the letter ‘e‘.
where,
Read More: Eccentricity Standard Equation of HyperbolaThe standard equations of a hyperbola are:
A hyperbola has two standard equations. These equations of a hyperbola are based on its transverse axis and conjugate axis.
Latus Rectum of HyperbolaLatus rectum of a hyperbola is a line passing through any of the foci of a hyperbola and perpendicular to the transverse axis of the hyperbola. The endpoints of a latus rectum lie on the hyperbola, and its length is 2b2/a. Derivation of Hyperbola EquationLet us consider a point P on the hyperbola whose coordinates are (x, y). From the definition of the hyperbola, we know that the difference between the distance of point P from the two foci F and F’ is 2a, i.e., PF’-PF = 2a. Let the coordinates of the foci be F (c, o) and F ‘(-c, 0).
Now, by using the coordinate distance formula, we can find the distance of point P (x, y) to the foci F (c, 0) and F ‘(-c, 0).
Similarly, we can derive the standard equations of the other hyperbola, i.e., [y2/a2 – x2/b2] = 1 Hyperbola FormulaFollowing hyperbola formulas are widely used in finding the various parameters of the hyperbola which include, the equation of hyperbola, the major and minor axis, eccentricity, asymptotes, vertex, foci, and semi-latus rectum.
Where,
Graph of HyperbolaHyperbola is a curve which has two unbounded curves which are mirror images of each other. The graph of the hyperbola shows that curve in the 2-D plane. We can observe the different parts of a hyperbola in the hyperbola graphs for standard equations given below:
Conjugate HyperbolaConjugate Hyperbola are 2 hyperbolas such that the transverse and conjugate axes of one hyperbola are the conjugate and transverse axis of the other hyperbola respectively. Conjugate hyperbola of (x2 / a2) – (y2 /b2) = 1 is,
Where,
Properties of Hyperbola
Auxiliary Circles of HyperbolaAuxiliary Circle is a circle which is drawn with centre C and diameter as a transverse axis of the hyperbola. The auxiliary circle of the hyperbola equation is,
Rectangular HyperbolaA hyperbola with a transverse axis of 2a units and a conjugate axis of 2b units of equal length is called the Rectangular Hyperbola. i.e. in rectangular hyperbola, 2a = 2b ⇒ a = b Equation of a Rectangular Hyperbola is given as follows:
Note: Eccentricity of Rectangular hyperbola is √2. Parametric Representation of HyperbolaParametric Representation of auxiliary circles of the hyperbola is:
People Also ReadHyperbola Class 11In Class 11 mathematics, the study of hyperbolas forms a part of the conic sections in analytic geometry. Understanding hyperbolas at this level involves exploring their definition, standard equations, properties, and various elements associated with them. Class 11 curriculum typically includes deriving these equations and properties, sketching hyperbolas based on given equations, and solving problems related to the hyperbola’s elements and positions. Mastery of these concepts provides a strong foundation in analytic geometry, preparing students for further studies in mathematics and related fields. Summary – HyperbolaA hyperbola is a type of conic section that forms when a plane intersects a cone at an angle such that two separate curves are produced. Characterized by its mirror symmetry, a hyperbola consists of two disconnected branches, each curving away from the other. It can be defined mathematically in a coordinate plane using a standard equation, which varies based on its orientation—either horizontal or vertical—and whether its center is at the origin or another point. The standard forms are x2/a2 – y2/b2 = 1 for a hyperbola opening horizontally and y2/a2 – x2/b2 = 1 for one opening vertically, with variations to accommodate a center moved to (h,k). Key features of hyperbolas include vertices, the closest points on each branch to the center; foci, points from which distances to any point on the hyperbola have a constant difference; and asymptotes, lines that the branches approach but never touch. The properties of hyperbolas make them significant in various fields, including astronomy, physics, and engineering, for modeling and analyzing hyperbolic trajectories and behaviors. Solved Examples on HyperbolaQuestion 1: Determine the eccentricity of the hyperbola x2/64 – y2/36 = 1. Solution:
Question 2: If the equation of the hyperbola is [(x-4)2/25] – [(y-3)2/9] = 1, find the lengths of the major axis, minor axis, and latus rectum. Solution:
Question 3: Find the vertex, asymptote, major axis, minor axis, and directrix if the hyperbola equation is [(x-6)2/72]-[(y-2)2/42] = 1. Solution:
Question 4: Find the eccentricity of the hyperbola whose latus rectum is half of its conjugate axis. Solution:
Practice Problems on HyperbolaP1. Find the standard form equation of the hyperbola with vertices at (-3, 2) and (1, 2), and a focal length of 5. P2. Determine the center, vertices, and foci of the hyperbola with the equation 9x2 – 4y2 = 36. P3. Given the hyperbola with the equation (x – 2)2/16 – (y + 1)2/9 = 1, find the coordinates of its center, vertices, and foci. P4. Write the equation of the hyperbola with a horizontal major axis, center at (0, 0), a vertex at (5, 0), and a focus at (3, 0). Hyperbola – FAQsWhat is Hyperbola in Maths?
What is Standard Equation of Hyperbola?
What is Eccentricity of Hyperbola?
What is Formula of Eccentricity of Hyperbola?
What are Foci of Hyperbola?
What is Transverse Axis of Hyperbola?
What are Asymptotes of Hyperbola?
How many Asymptotes does Hyperbola have?
What is Hyperbola used for?
What is Difference between Parabola and Hyperbola in Standard Form?
What is Basic Equation of Hyperbola Graph?
What are Types of Hyperbola?
How do you identify a Hyperbola equation?
What is formula of B in Hyperbola?
How to draw a Hyperbola?
|
Reffered: https://www.geeksforgeeks.org
| Class 11 |
Type: | Geek |
Category: | Coding |
Sub Category: | Tutorial |
Uploaded by: | Admin |
Views: | 11 |