|
|
Parabola is one of the conic sections in Maths. It is an intersection of a surface plane and a double-napped cone. A parabola is a U-shaped curve that can be either concave up or down, depending on the equation. Parabolic curves are widely used in many fields such as physics, engineering, finance, and computer sciences. In this article, we will understand What a Parabola is, its Graph, Parabola Properties, Parabola Examples, Parabola Equation, and others in detail.
What is Parabola in Maths?Parabola is an equation of a specific curve, such that each point on the curve is always equidistant from a fixed point and a fixed-line. Parabola is the introductory curves in the study of conic section, as parabola and other conics can be obtained by slicing the double-napped cone (two identical cones stacked on top of each other from the vertex part) with the help of the surface plane at different angles. Parabola Definition
Parabola ShapeA parabola is a U-shaped curved line where every point on the line is at an equal distance from the focus and directrix of the parabola.  Parabola Table of Content
Equation of ParabolaEquation of Parabola can vary depending on its orientation and the position of its vertex, but one common form is:
Here, a, b, and c are constants. The shape of the parabola depends primarily on the value of a:
Standard Equation of ParabolaStandard Equation of Parabola is given as follows:
In this form, directrix is parallel to the y-axis. If directrix is parallel to the x-axis, then the standard equation of a parabola is given by,
If the parabolas are drawn in alternate quadrants, then their equation is given as y2 = -4ax and x2 = -4ay.
Vertex Form of a ParabolaGeneral equation of a parabola is given by y = a(x – h)2 + k or x = a(y – k)2 +h where (h, k) denotes the vertex of the parabola.
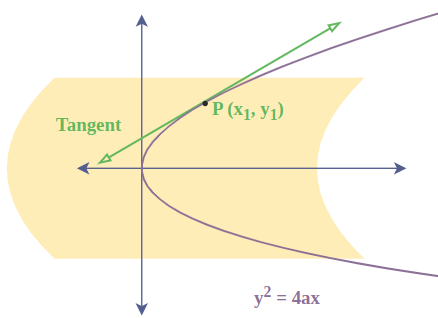
Parametric Coordinates of a ParabolaFor a parabola, y2 = 4ax, if we take x = at2 and y = 2at for any value of “t” they will satisfy the equation of a parabola, the coordinates (at2, 2at) is termed as parametric coordinate, and “t” is called as the parameter. Thus, x = at2 and y = 2at are called the parametric equations of the parabola y2 = 4ax Similarly, parametric form of the parabola x2 = 4ay are x = 2at, y = at2 Equation of Tangent to a ParabolaTangents are lines that touch the curve only at a single point. So a line that touches the parabola exactly at one single point is called the tangent to a parabola.
There are various ways to find the tangent of a parabola which are discussed in next sections. Equation of Tangent in Point FormFor the given parabola y2 = 4ax equation of the tangent at point (x1, y1) is given by:
where, (x1, y1) is the point of contact between the tangent and the curve. Equation of Tangent in Parametric FormFor the given parabola y2 = 4ax equation of the tangent at point (at2, 2at) is given by:
where, (at2, 2at) is the point of contact between the tangent and the curve. Equation of Tangent in Slope FormFor the given parabola y2 = 4ax with slope m equation of the tangent at point (a/m2, 2a/m) is given by
where, (a/m2, 2a/m) is the point of contact between the tangent and the curve. Pair of Tangent from an External PointPair of tangents from an external point to any conic is given by SS1 = T2 where for parabola y2 = 4ax, S = y2 – 4ax, S1 = y12 -4ax1 and T = yy1 – 2a(x + x1). Thus, the equation of pair of tangents from an external point becomes:
Director Circle of ParabolaDirector circle is the geometric object related to the conic section and is defined as the locus of the intersection of the pair perpendicular tangent of any conic. For the parabola, the director circle is the directrix as all the perpendicular pairs of tangents of the parabola intersect each other at the directrix.
Chord of ContactChord of contact of the parabola is a secant line joining the point of tangency for the tangents drawn from the external point on the parabola. For parabola y2 = 4ax, chord of contact is given by T = 0, where T = yy1 – 2a(x + x1). Therefore the equation of chord of contact is given
Where, (x1, y1) is the external point from which both the tangents are drawn to the parabola.
Equation of Normal to a ParabolaA line perpendicular to the tangent of the parabola at the point of tangency is known as the normal of the parabola. As this line is perpendicular to the tangent at the point of tangency to the parabola, the equation of this line can be found easily if the equation of tangent and point of tangency is given, using the concept of the equation of line perpendicular to the given line, but this is not always the case.
The equation of normal is given in three ways as follows: Equation of Normal in Slope FormFor a parabola y2 = 4ax and m is the slope of normal at the point of contact (am2, -2am), the equation of normal is given by:
Equation of Normal in Point FormFor a parabola y2 = 4ax, equation of normal at (x1, y1) is given as follows:
Equation of Normal in Parametric FormFor a parabola y2 = 4ax, the equation of normal at the point (at2, 2at) [where t is the parameter] is given as follows:
Parabola FormulasSome important parabola formulas are added in the table below:
Articles Related to Parabola:Derivation of Parabola EquationTake a point P with coordinates (x, y) on the parabola which lies on the X-Y plane. By the definition of the parabola, the distance of any point on the parabola from the focus and from the directrix is equal. Now distance of P from the directrix is given by PB where the coordinates of B are (-a, y) as it lies on the directrix, and the distance of P from focus is PF. Image of parabola is shown below,
By the definition of parabola, PF = PB . . . .(1) Using Distance Formula, we get PF = √(x-a)2+(y-0)2= √{(x-a)2+y2} . . . .(2) PB = √{(x+a)2} . . . .(3) By using, equations (1), (2), and (3), we get √{(x-a)2+y2} = √{(x+a)2} ⇒ (x – a)2 + y2 = (x + a)2 ⇒ x2 + a2 – 2ax + y2 = x2 + a2 + 2ax ⇒ y2 – 2ax = 2ax
Which is the required equation of the parabola. Similarly, the equation for other parabolas i.e., x2 = 4ay, y2 = -4ax, and x2 = -4ay, can also be proved. Graph of ParabolaGraph of the parabola is a U-shaped curve, which can open either in an upward direction or in a downward direction. Generally, the equation of a parabola which is graphed is written in the form of y = ax2 + bx + c, where a, b, and c are constants that define the shape of the parabola. If a > 0, in the above equation, the parabola opens in an upward direction and its vertex is the lowest point of the parabola, and if a<0, then the parabola opens in a downward direction and its vertex is the highest point in the parabola. Vertex of the parabola is also the point from where the only line of symmetry of the parabola passes. Position of Point Relative to the ParabolaPosition of a point A (x1, y1) relative to the parabola y2 = 4ax, can be shown using the S1 = y2 – 4ax, Case 1: If S1 = 0, for any point A, then Point A lies on the parabola. Case 2: If S1 < 0, for any point A, then Point A lies inside the parabola. Case 3: If S1 > 0, for any point A, then Point A lies outside the parabola. Intersection with Straight LineFor a parabola y2 = 4ax, any straight-line y = mx + c, can almost intersect the parabola at two points. For the intersection of the line and parabola, put y = mx + c in the equation of the parabola,
Case 1: Discriminant > 0:
Case 2: Discriminant = 0:
Case 3: Discriminant < 0:
Properties of Parabola
Important Terms Related to Parabola
Parabola Solved ExamplesExample 1: Find coordinates of the focus, axis, the equation of the directrix, and latus rectum of the parabola y2 = 16x. Solution:
Example 2: Find the equation of the parabola which is symmetric about the y-axis, and passes through the point (3, -4). Solution:
Example 3: Find coordinates of the focus, axis, and the equation of the directrix and latus rectum of the parabola y2 = 8x. Solution:
Example 4: Find the coordinates of the focus, axis, the equation of the directrix, and latus rectum of the parabola y2 = 52x. Solution:
Example 5: Find coordinates of the focus, axis, the equation of the directrix, and latus rectum of the parabola x2 = 16y. Solution:
Practice Questions on ParabolaQ1. Find the vertex, focus, and directrix of the parabola with the equation y = x2 – 4x + 3y = x2 – 4x + 3. Q2. Determine whether the parabola with the equation y = -2x2 + 4x – 1y = -2x2 + 4x – 1 opens upward or downward, and find its vertex. Q3. Given the equation 4x2 – 16y = 0, 4x2 – 16y = 0, rewrite it in standard form and find the vertex, focus, and directrix of the parabola. Q4. Solve for xx in the equation 2x2 – 3x – 5 = 0, 2x2 – 3x – 5 = 0, and determine the nature of the roots with respect to the corresponding parabola. Also Read: ConclusionUnderstanding the properties and applications of parabolas is essential in both theoretical and applied mathematics. Their unique geometric characteristics and reflective properties make them a fascinating topic with wide-ranging applications in various fields. Whether grappling with parabola motion, designing architectural elements, or studying the nature of conic sections, the parabola remains a key concept. A parabola is a fundamental concept in mathematics, particularly in the study of quadratic functions and conic sections. Its distinct U-shaped curve is defined by a quadratic equation and exhibits unique properties such as symmetry and a focal point, which have wide-ranging applications in various fields. Parabola in Maths – FAQsWhat is Parabola?
What is meant by Conjugate Axis of a Parabola?
What are Applications of Parabola?
What is Shape of a Parabola?
What is Eccentricity of a Parabola?
What is Formula for Length of Latus Rectum of a Parabola?
What is Vertex of a Parabola?
What is a Parabolic motion?
What are 4 Types of Parabola?
What is difference between Parabola and Hyperbola?
What are 4 key Features of a Parabola?
Who invented Parabola?
|
Reffered: https://www.geeksforgeeks.org
| Class 11 |
Type: | Geek |
Category: | Coding |
Sub Category: | Tutorial |
Uploaded by: | Admin |
Views: | 13 |