Maximize difference between pair of nodes in a given rooted tree such that one node is ancestor of another - Coding

Given a Generic Tree consisting of N nodes valued from 0 to (N – 1) where P[i]^thin the array P[] denotes i^th nodes parent(1-based indexing). Each i^th node has a weight attached to it, given in the array W[]. The task is to find a pair of nodes (u, v), such that u is an ancestor of v, and W_u – W_v is maximized.

Note: In the array P[], -1 denotes the root node. If there’s a single node, then print -1.

Examples:

Input: N = 4, W[] = {5, 10, 6, 12}, P[] = {2, -1, 4, 2}
Output: 6
Explanation: The tree with weight will be:

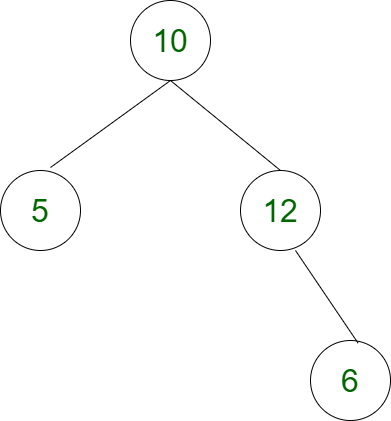
Here, 4^th node having weight 12 and 3^rd node having weight 6, the difference will be (12 – 6) = 6.

Input: N = 1, W = { 30 }, P = { -1 }
Output: -1

Approach: The given problem can be solved by using the Breadth-First Search on the N-ary Tree to mark the ancestor number for the given tree P[], and then using DFS Traversal and find the maximum difference maxDiff, by considering every node as an ancestor with its corresponding nodes having less number ancestor value. Follow the steps below to solve the problem:

Define a function dfs(int src, int val, vector<int> & W) and perform the following tasks:
- Set the value of visited[src] as true.
- Iterate over the range [0, size) where size is the size of the row tree[cur] using the variable neighbor and performs the following tasks:
  - If visited[neighbor] is false and ancestor[neighbor] is greater than ancestor[src] then set the value of maxDiff as the maximum of maxDiff or val – W[neighbor-1].
  - Call the function dfs(neighbor, val, W).
Define a function bfs(int src, int N) and perform the following tasks:
- Assign the vector visited[N + 1] with values false.
- Initialize a queue q[].
- Set the value of ancestorNum[src] as 0 and visited[src] as true.
- Enqueue the value src into the queue q[].
- Traverse in a while loop till queue q[] is not empty and perform the following tasks:
  - Initialize the variable cur as the front element of the queue q[] and dequeue from the queue q[].
  - Iterate over the range [0, size) where size is the size of the row tree[cur] using the variable neighbor and if visited[neighbor] is false then set it as true and enqueue it into the queue q[] and set the value of ancestor[neighbor] as (ancestor[cur] + 1).
Initialize the vectors tree[][], visited[] and ancestorNum[].
Initialize the variable maxDiff as INT_MIN to store the answer.
Resize the vector tree[][] to size (N + 1).
Assign vectors visited[N + 1] with value false and ancestorNum[N+1] with value 0.
Initialize the variable src.
Iterate over the range [0, N) using the variable i and if P[I] is -1, then set the value of src as i. Otherwise, push the value P[I] in the row i+1 and value i + 1 in the row P[I] into the vector tree[][].
Call the function bfs(src, N+1) to perform breadth-first search.
Assign vector visited[N+1] with value false.
Call the function dfs(src, W[src], W) to perform depth-first search.
Iterate over the range [0, N) using the variable i and perform the following steps:
- If i equals src, then continue. Otherwise, assign vector visited[N+1] with value false.
- Call the function dfs(i+1, W[i], W).
After performing the above steps, print the value of maxDiff as the answer.

Below is the implementation of the above approach:

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
vector<vector<int> > tree;
vector<bool> visited;
vector<int> ancestorNum;
 
// Stores the maximum difference
int maxDiff = INT_MIN;
 
// DFS traversal for source node as src
void dfs(int src, int val, vector<int>& W)
{
 
    // Mark src node as visited
    visited[src] = true;
 
    // Traverse the tree
    for (auto neighbour : tree[src]) {
 
        // Check neighbour node is not
        // visited and ancestorNum should
        // be greater than the src node
        if (!visited[neighbour]
            && (ancestorNum[neighbour]
                > ancestorNum[src])) {
 
            // Update the maxDiff
            maxDiff = max(
                val - W[neighbour - 1],
                maxDiff);
 
            // Recurrence call for dfs
            dfs(neighbour, val, W);
        }
    }
}
 
// BFS traversal for source node as src
void bfs(int src, int N)
{
    // Initially mark all node as
    // not visited
    visited.assign(N, false);
 
    // Stores the nodes
    queue<int> q;
 
    // Initially for src node mark
    // ancestorNum as 0
    ancestorNum[src] = 0;
 
    // Mark src as visited
    visited[src] = true;
 
    // Push src node into the q
    q.push(src);
 
    // Traverse the queue q
    while (!q.empty()) {
 
        // Pop front element of the q
        int cur = q.front();
        q.pop();
 
        // Traverse the tree
        for (auto neighbour : tree[cur]) {
 
            // Check neighbour node is
            // already not visited
            if (!visited[neighbour]) {
 
                // Mark the neighbour
                // node as visited
                visited[neighbour] = true;
 
                // Push the neighbour
                // node into the q
                q.push(neighbour);
 
                // Update the neighbour
                // node ancestorNum
                ancestorNum[neighbour]
                    = ancestorNum[cur] + 1;
            }
        }
    }
}
 
// Function to find the maximized
// difference between two pair of nodes
// in rooted tree such that one node
// is ancestor of another node
void maximumDiff(vector<int> W,
                 vector<int> P, int N)
{
    if (N == 1) {
        cout << "-1\n";
        return;
    }
 
    // Resize the tree
    tree.resize(N + 1);
 
    // Mark all the nodes as not visited
    visited.assign(N + 1, false);
 
    // Assign all the node values
    // for ancestorNum to 0
    ancestorNum.assign(N + 1, 0);
 
    // Stores the source node to traverse
    int src;
 
    for (int i = 0; i < N; i++) {
 
        // Check P[i] is -1
        if (P[i] == -1)
 
            // Update the source node src
            src = i;
 
        else {
 
            // Store the tree values
            tree[i + 1].push_back(P[i]);
            tree[P[i]].push_back(i + 1);
        }
    }
 
    // BFS from the source node src
    bfs(src, N + 1);
 
    // Mark all the nodes as not visited
    visited.assign(N + 1, false);
 
    // DFS Call for source node src
    dfs(src, W[src], W);
 
    // For every node call dfs function
    for (int i = 0; i < N; i++) {
 
        // Check i is root node
        if (i == src)
            continue;
 
        // Mark all the nodes as
        // not visited
        visited.assign(N + 1, false);
 
        // DFS Call for source
        // node as i+1
        dfs(i + 1, W[i], W);
    }
 
    // Print the maxDiff
    cout << maxDiff << endl;
}
 
// Driver Code
int main()
{
    vector<int> W = { 5, 10, 6, 12 };
    vector<int> P = { 2, -1, 4, 2 };
    int N = P.size();
 
    maximumDiff(W, P, N);
 
    return 0;
}

Java

// Java program for the above approach
import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
 
public class Main {
    private static ArrayList<ArrayList<Integer> > tree;
    private static boolean[] visited;
    private static int[] ancestorNum;
    private static int maxDiff = Integer.MIN_VALUE;
    private static void dfs(int src, int val, int[] W)
    {
        visited[src] = true;
        // Check neighbour node is not
        // visited and ancestorNum should
        // be greater than the src node
        for (int neighbour : tree.get(src)) {
            if (!visited[neighbour]
                && ancestorNum[neighbour]
                       > ancestorNum[src]) {
                maxDiff = Math.max(val - W[neighbour - 1],
                                   maxDiff);
                dfs(neighbour, val, W);
            }
        }
    }
 
    private static void bfs(int src, int N)
    {
        visited = new boolean[N];
        Arrays.fill(visited, false);
        Queue<Integer> q = new LinkedList<>();
        ancestorNum[src] = 0;
        visited[src] = true;
        q.offer(src);
        while (!q.isEmpty()) {
            int cur = q.poll();
            for (int neighbour : tree.get(cur)) {
                if (!visited[neighbour]) {
                    visited[neighbour] = true;
                    q.offer(neighbour);
                    ancestorNum[neighbour]
                        = ancestorNum[cur] + 1;
                }
            }
        }
    }
    // Function to find the maximized
    // difference between two pair of nodes
    // in rooted tree such that one node
    // is ancestor of another node
    private static void maximumDiff(int[] W, int[] P, int N)
    {
        if (N == 1) {
            System.out.println("-1");
            return;
        }
 
        tree = new ArrayList<>();
        for (int i = 0; i <= N; i++)
            tree.add(new ArrayList<>());
 
        int src = 0;
        for (int i = 0; i < N; i++) {
            if (P[i] == -1) {
                src = i;
            }
            else {
                tree.get(i + 1).add(P[i]);
                tree.get(P[i]).add(i + 1);
            }
        }
        // Assign all the node values
        // for ancestorNum to 0
        ancestorNum = new int[N + 1];
        bfs(src, N + 1);
 
        Arrays.fill(visited, false);
        dfs(src, W[src], W);
        // For every node call dfs function
        for (int i = 0; i < N; i++) {
            // Check i is root node
            if (i == src)
                continue;
            Arrays.fill(visited, false);
            dfs(i + 1, W[i], W);
        }
 
        System.out.println(maxDiff);
    }
 
    public static void main(String[] args)
    {
        int[] W = { 5, 10, 6, 12 };
        int[] P = { 2, -1, 4, 2 };
        int N = P.length;
 
        maximumDiff(W, P, N);
    }
}

Python3

# Python 3 program for the above approach
 
tree = []
visited = []
ancestorNum = []
 
import sys
 
# Stores the maximum difference
maxDiff = -sys.maxsize - 1
 
# DFS traversal for source node as src
def dfs(src, val, W):
    global ancestorNum
    global visited
    global tree
    global maxDiff
    # Mark src node as visited
    visited[src] = True
 
    # Traverse the tree
    for neighbour in tree[src]:
        # Check neighbour node is not
        # visited and ancestorNum should
        # be greater than the src node
        if (visited[neighbour] == False and (ancestorNum[neighbour]> ancestorNum[src])):
 
            # Update the maxDiff
            maxDiff = max(val - W[neighbour - 1],maxDiff)
 
            # Recurrence call for dfs
            dfs(neighbour, val, W)
 
# BFS traversal for source node as src
def bfs(src,N):
    global ancestorNum
    global visited
    global tree
    # Initially mark all node as
    # not visited
    visited = [False for i in range(N)]
 
    # Stores the nodes
    q = []
 
    # Initially for src node mark
    # ancestorNum as 0
    ancestorNum[src] = 0
 
    # Mark src as visited
    visited[src] = True
 
    # Push src node into the q
    q.append(src)
 
    # Traverse the queue q
    while (len(q)>0):
 
        # Pop front element of the q
        cur = q[0]
        q = q[1:]
 
        # Traverse the tree
        for neighbour in tree[cur]:
            # Check neighbour node is
            # already not visited
            if (visited[neighbour]==False):
 
                # Mark the neighbour
                # node as visited
                visited[neighbour] = True
 
                # Push the neighbour
                # node into the q
                q.append(neighbour)
 
                # Update the neighbour
                # node ancestorNum
                ancestorNum[neighbour] = ancestorNum[cur] + 1
 
# Function to find the maximized
# difference between two pair of nodes
# in rooted tree such that one node
# is ancestor of another node
def maximumDiff(W, P, N):
    global ancestorNum
    global visited
    global tree
    if (N == 1):
        print("-1")
        return
 
    # Resize the tree
    tree = [[] for i in range(N+1)]
 
    # Mark all the nodes as not visited
    visited = [False for i in range(N + 1)]
 
    # Assign all the node values
    # for ancestorNum to 0
    ancestorNum = [0 for i in range(N + 1)]
 
    # Stores the source node to traverse
    src = 0
 
    for i in range(N):
        # Check P[i] is -1
        if (P[i] == -1):
            # Update the source node src
            src = i
 
        else:
 
            # Store the tree values
            tree[i + 1].append(P[i])
            tree[P[i]].append(i + 1)
 
    # BFS from the source node src
    bfs(src, N + 1)
 
    # Mark all the nodes as not visited
    visited = [False for i in range(N+1)]
 
    # DFS Call for source node src
    dfs(src, W[src], W)
 
    # For every node call dfs function
    for i in range(N):
        # Check i is root node
        if (i == src):
            continue
 
        # Mark all the nodes as
        # not visited
        visited = [False for i in range(N+1)]
 
        # DFS Call for source
        # node as i+1
        dfs(i + 1, W[i], W)
 
    # Print the maxDiff
    print(maxDiff)
 
# Driver Code
if __name__ == '__main__':
    W = [5, 10, 6, 12]
    P = [2, -1, 4, 2]
    N = len(P)
    maximumDiff(W, P, N)
     
    # This code is contributed by SURENDRA_GANGWAR.

C#

// C# program for the above approach
using System;
using System.Collections.Generic;
 
// Stores the maximum difference
class Program
{
 
  // Stores the maximum difference
  static int maxDiff = int.MinValue;
  static List<List<int>> tree = new List<List<int>>();
  static bool[] visited;
  static int[] ancestorNum;
 
  // DFS traversal for source node as src
  static void DFS(int src, int val, int[] W)
  { 
 
    // Mark src node as visited
    visited[src] = true;
 
    // Traverse the tree
    foreach (int neighbour in tree[src])
 
      // Check neighbour node is not
      // visited and ancestorNum should
      // be greater than the src node
    {
      if (!visited[neighbour] && ancestorNum[neighbour] > ancestorNum[src])
      {
 
        // Update the maxDiff
        maxDiff = Math.Max(val - W[neighbour - 1], maxDiff);
 
        // Recurrence call for dfs
        DFS(neighbour, val, W);
      }
    }
  }
 
  // BFS traversal for source node as src
  static void BFS(int src, int N)
  {
 
    // Initially mark all node as
    // not visited
    visited = new bool[N];
 
    // Initially for src node mark
    // ancestorNum as 0
    Queue<int> q = new Queue<int>();
 
    ancestorNum = new int[N];
    ancestorNum[src] = 0;
    visited[src] = true;
    q.Enqueue(src);
 
    while (q.Count > 0)
    {
      int cur = q.Dequeue();
      foreach (int neighbour in tree[cur])
      {
        if (!visited[neighbour])
        {
          visited[neighbour] = true;
          q.Enqueue(neighbour);
          ancestorNum[neighbour] = ancestorNum[cur] + 1;
        }
      }
    }
  }
 
  static void MaximumDiff(int[] W, int[] P, int N)
  {
    if (N == 1)
    {
      Console.WriteLine("-1");
      return;
    }
 
    tree = new List<List<int>>();
    for (int i = 0; i <= N; i++)
    {
      tree.Add(new List<int>());
    }
 
    int src = 0;
    for (int i = 0; i < N; i++)
    {
      if (P[i] == -1)
      {
        src = i;
      }
      else
      {
        tree[i + 1].Add(P[i]);
        tree[P[i]].Add(i + 1);
      }
    }
 
    BFS(src, N + 1);
    visited = new bool[N + 1];
    DFS(src, W[src], W);
 
    for (int i = 0; i < N; i++)
    {
      if (i == src)
        continue;
 
      visited = new bool[N + 1];
      DFS(i + 1, W[i], W);
    }
 
    Console.WriteLine(maxDiff);
  }
 
  // Driver Code
  static void Main(string[] args)
  {
    int[] W = { 5, 10, 6, 12 };
    int[] P = { 2, -1, 4, 2 };
    int N = P.Length;
 
    MaximumDiff(W, P, N);
  }
}

Javascript

       // JavaScript code for the above approach
       let tree = [];
       let visited = [];
       let ancestorNum = [];
 
       // Stores the maximum difference
       let maxDiff = Number.MIN_SAFE_INTEGER;
 
       // DFS traversal for source node as src
       function dfs(src, val, W)
       {
        
           // Mark src node as visited
           visited[src] = true;
 
           // Traverse the tree
           for (let neighbour of tree[src])
           {
            
               // Check neighbour node is not
               // visited and ancestorNum should
               // be greater than the src node
               if (!visited[neighbour] && ancestorNum[neighbour] > ancestorNum[src]) {
                   // Update the maxDiff
                   maxDiff = Math.max(val - W[neighbour - 1], maxDiff,6);
 
                   // Recurrence call for dfs
                   dfs(neighbour, val, W);
               }
           }
       }
 
       // BFS traversal for source node as src
       function bfs(src, N) {
           // Initially mark all node as
           // not visited
           visited = Array(N).fill(false);
 
           // Stores the nodes
           let q = [];
 
           // Initially for src node mark
           // ancestorNum as 0
           ancestorNum[src] = 0;
 
           // Mark src as visited
           visited[src] = true;
 
           // Push src node into the q
           q.push(src);
 
           // Traverse the queue q
           while (q.length > 0) 
           {
            
               // Pop front element of the q
               let cur = q.shift();
 
               // Traverse the tree
               for (let neighbour of tree[cur]) 
               {
                
                   // Check neighbour node is
                   // already not visited
                   if (!visited[neighbour])
                   {
                    
                       // Mark the neighbour
                       // node as visited
                       visited[neighbour] = true;
 
                       // Push the neighbour
                       // node into the q
                       q.push(neighbour);
 
                       // Update the neighbour
                       // node ancestorNum
                       ancestorNum[neighbour] = ancestorNum[cur] + 1;
                   }
               }
           }
       }
 
 
       // Function to find the maximized
       // difference between two pair of nodes
       // in rooted tree such that one node
       // is ancestor of another node
       function maximumDiff(W, P, N) {
           if (N === 1) {
               console.log("-1");
               return;
           }
 
           // Resize the tree
           tree= new Array(N + 1);
           tree.fill([]);
 
           // Mark all the nodes as not visited
           visited = Array(N + 1).fill(false);
 
           // Assign all the node values
           // for ancestorNum to 0
           ancestorNum.length = N + 1;
           ancestorNum.fill(0);
 
           // Stores the source node to traverse
           let src = 0;
 
           for (let i = 0; i < N; i += 1) {
               // Check P[i] is -1
               if (P[i] === -1) {
                   // Update the source node src
                   src = i;
               } else {
                   // Store the tree values
                   tree[i + 1].push(P[i]);
                   tree[P[i]].push(i + 1);
               }
           }
 
           // BFS from the source node src
           bfs(src, N + 1);
 
           // Mark all the nodes as not visited
           visited = Array(N + 1).fill(false);
 
           // DFS Call for source node src
           dfs(src, W[src], W);
 
           // For every node call dfs function
           for (let i = 0; i < N; i += 1) {
               // Check i is root node
               if (i === src) continue;
 
               // Mark all the nodes as
               // not visited
               visited = Array(N + 1).fill(false);
 
               // DFS Call for source
               // node as i+1
               dfs(i + 1, W[i], W);
           }
 
           // Print the maxDiff
           console.log(maxDiff);
       }
 
       // Test the code
       maximumDiff([5, 10, 6, 12], [2, -1, 4, 2], 4);
 
// This code is contributed by Potta Lokesh

Output:

Time Complexity: O(N²)
Auxiliary Space: O(N)

Reffered: https://www.geeksforgeeks.org

Tree

Related
Maximize sum of paths from LCA of nodes u and v to one of those nodes
Count number of nodes in a complete Binary Tree
Minimum path need to reverse to reach each node in a tree from each vertex
ZigZag Level Order Traversal of an N-ary Tree
Minimum distance between two given nodes in an N-ary tree

Type:	Geek
Category:	Coding
Sub Category:	Tutorial
Uploaded by:	Admin
Views:	12